La fonction logarithme
Exercices types : ème partie - Exercice 2
30 min
45
Soit la fonction définie sur par : . On note la courbe représentative de la fonction .
On note la fonction dérivée de la fonction sur .
On note la fonction dérivée de la fonction sur .
Question 1
Partie A
Justifier que
Correction
est dérivable sur .
Ici on reconnaît la forme : avec ; ; et enfin . Ainsi : ; ; et .
Il vient alors que :
Ainsi :
Ici on reconnaît la forme : avec ; ; et enfin . Ainsi : ; ; et .
Il vient alors que :
Ainsi :
Question 2
Calculer , où est la dérivée seconde de .
Correction
Comme alors . Nous allons tout mettre au même dénominateur.
Il en résulte que :
Il en résulte que :
Question 3
Etudier le signe de , en déduire le tableau de variation de sur l'intervalle .
Correction
Pour tout réel appartenant à l'intervalle , on sait que est strictement positif.
Donc le signe de dépend alors du numérateur .
alors .
Cela signifie que :
lorsque lorsque Nous traduisons cela dans un tableau de variation, donné ci-dessous :
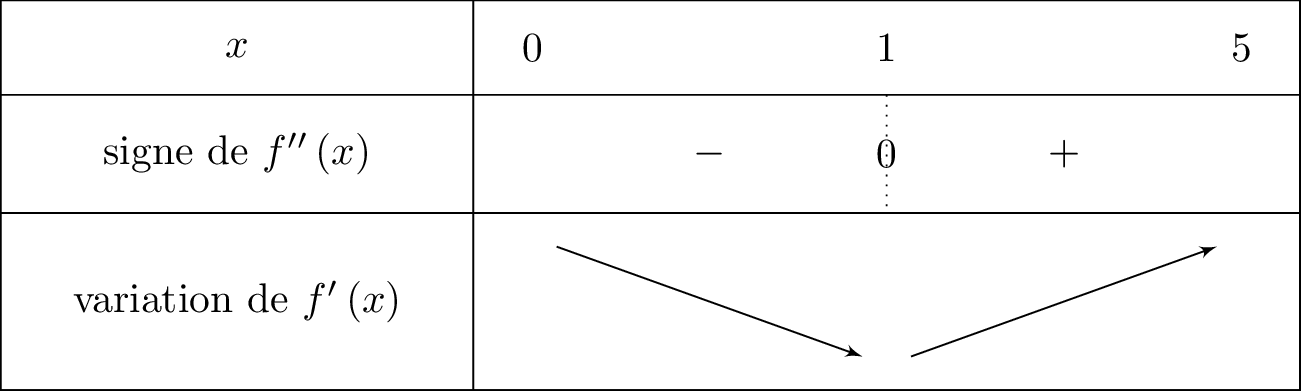
Donc le signe de dépend alors du numérateur .
alors .
Cela signifie que :

Question 4
Justifier le signe de , en déduire que la fonction est strictement croissante sur .
Correction
D'après le tableau de variation de , on vérifie facilement que admet un minimum lorsque . Calculons alors celui-ci.
Ainsi : .
 Il en résulte donc que la fonction admet un minimum qui vaut lorsque . Cela signifie que pour tout réel appartenant à l'intervalle , on a : .
Il en résulte donc que la fonction admet un minimum qui vaut lorsque . Cela signifie que pour tout réel appartenant à l'intervalle , on a : .
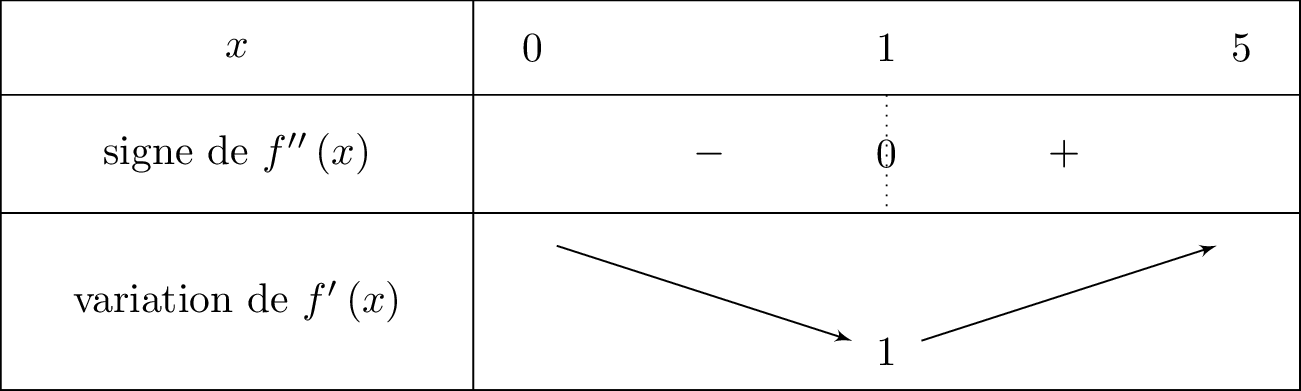
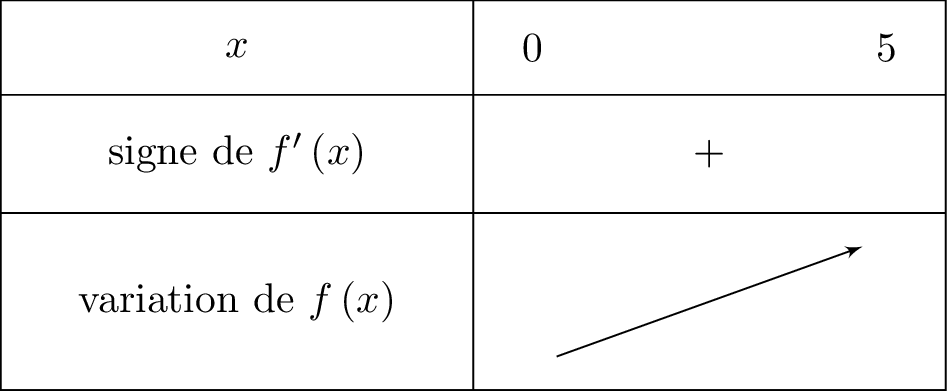
Finalement, la fonction est strictement croissante sur . Nous traduisons toute ces informations dans un tableau de variation, donné ci dessous :
Ainsi : .

Finalement, la fonction est strictement croissante sur . Nous traduisons toute ces informations dans un tableau de variation, donné ci dessous :

Question 5
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .1ère étape : calculer
2ème étape : calculer
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors :
.
Question 6
Partie B
Une entreprise produit et commercialise un article. Sa capacité de production quotidienne est limitée à milliers d'articles. La fonction modélise sur l'intervalle le coût total de production exprimé en milliers d'euros, où désigne le nombre de milliers d'articles fabriqués.
On note le coût moyen de production exprimé en euros, par article fabriqué.
est la fonction définie sur l'intervalle par . On admet que la fonction est dérivable sur l'intervalle et on appelle sa fonction dérivée tel que .
Une entreprise produit et commercialise un article. Sa capacité de production quotidienne est limitée à milliers d'articles. La fonction modélise sur l'intervalle le coût total de production exprimé en milliers d'euros, où désigne le nombre de milliers d'articles fabriqués.
On note le coût moyen de production exprimé en euros, par article fabriqué.
est la fonction définie sur l'intervalle par . On admet que la fonction est dérivable sur l'intervalle et on appelle sa fonction dérivée tel que .
Etudier les variations de sur .
Correction
Pour obtenir les variations de , il nous faut étudier le signe de .
Pour tout réel appartenant à l'intervalle , on sait que est strictement positif.
Donc le signe de dépend alors du numérateur .
Pour étudier le signe de , nous allons utiliser le discriminant.
Ainsi : ; et
, la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
De plus : D'où :
Le tableau de variation de est donné ci-dessous :
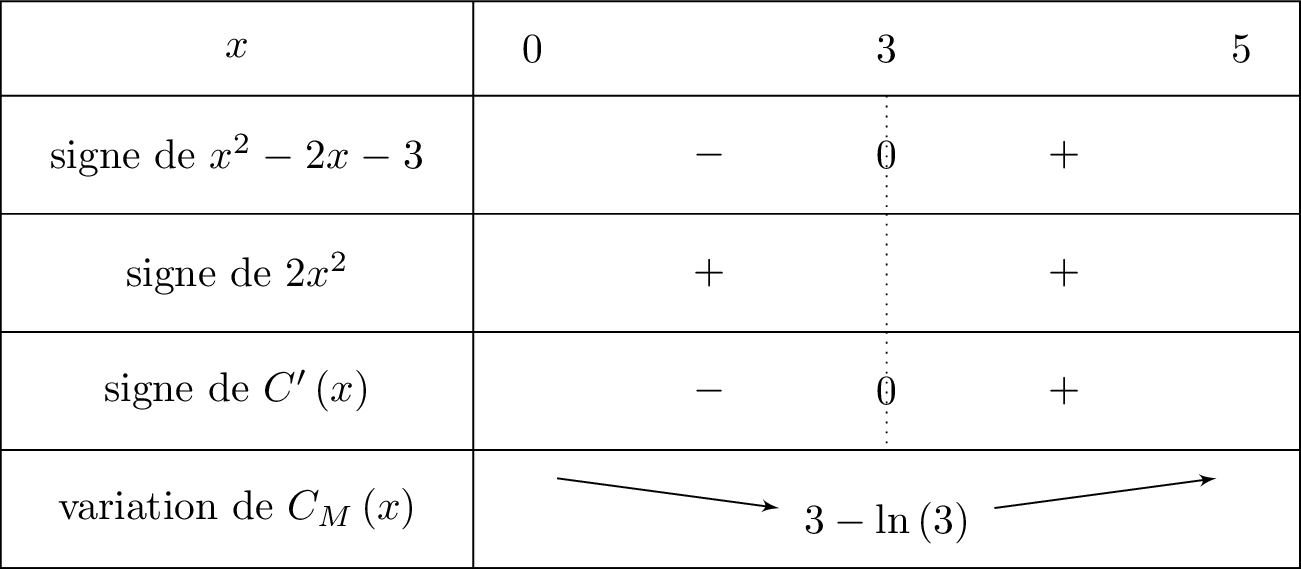
Pour tout réel appartenant à l'intervalle , on sait que est strictement positif.
Donc le signe de dépend alors du numérateur .
Pour étudier le signe de , nous allons utiliser le discriminant.
Ainsi : ; et
, la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
De plus : D'où :
Le tableau de variation de est donné ci-dessous :

Question 7
Déterminer la quantité d'articles à fabriquer pour que le coût moyen soit minimal. Déterminer alors, au centime d'euro près, ce coût moyen.
Correction
Pour que le coût soit minimal, il faut fabriquer articles. Ce coût moyen s'élève à euros.