La fonction logarithme
Exercices types : ère partie - Exercice 3
22 min
35
Question 1
Soit la fonction définie sur par : . On note la courbe représentative de la fonction .
Calculer les limites de aux bornes de son domaine de définition.
Correction
est dérivable sur .
Or pour tout réel appartenant à l'intervalle, on vérifie aisément que . Ainsi : .
La fonction est donc strictement croissante sur .
Nous traduisons cela dans un tableau de variation :
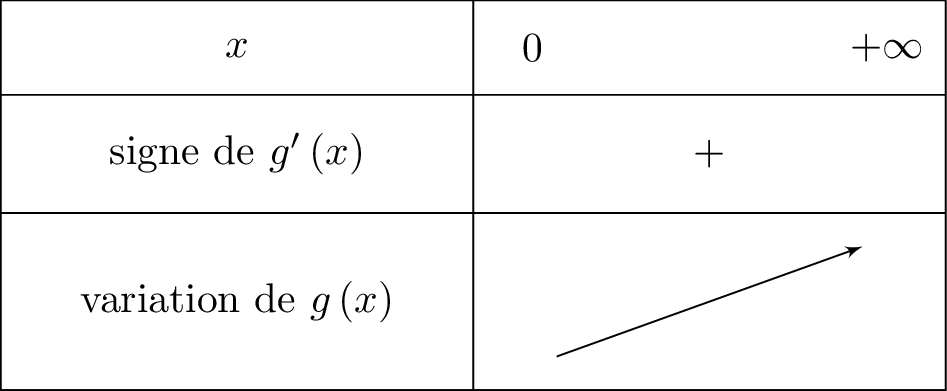
.
Or pour tout réel appartenant à l'intervalle, on vérifie aisément que . Ainsi : .
La fonction est donc strictement croissante sur .
Nous traduisons cela dans un tableau de variation :

Question 2
Calculer et en déduire le signe de sur l'intervalle .
Correction
Commençons par calculer .
d'où :
Nous intégrons cette information dans le tableau de variation ci-dessous :
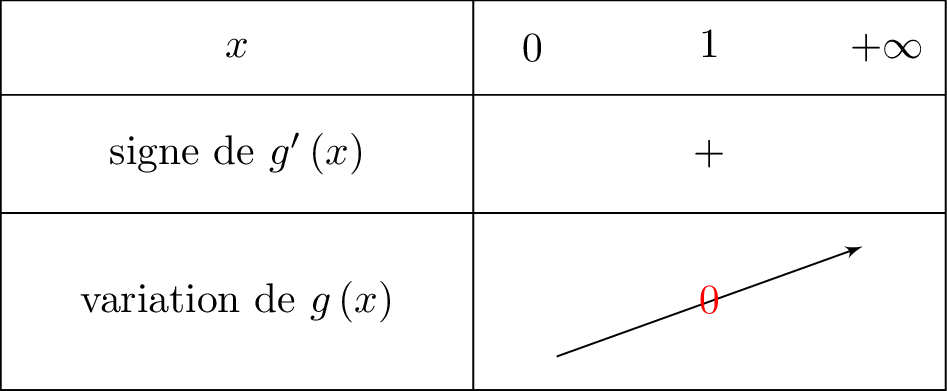 On a vu précédemment que .
On a vu précédemment que .
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :
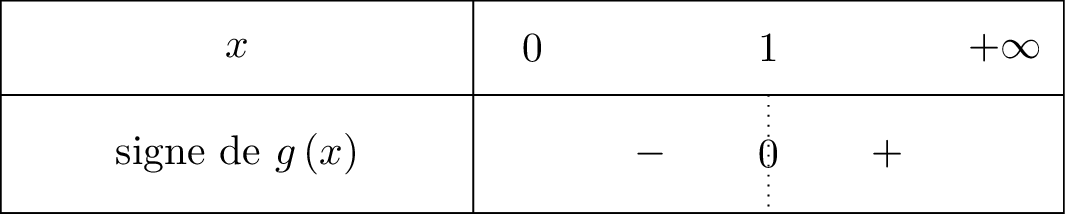
d'où :
Nous intégrons cette information dans le tableau de variation ci-dessous :
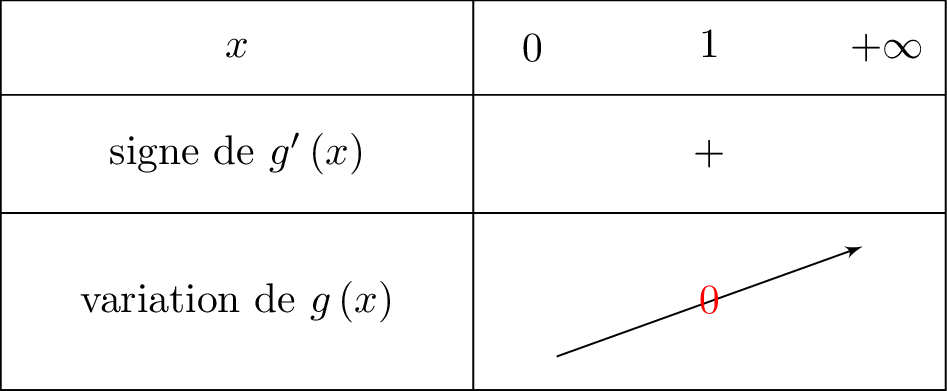
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :
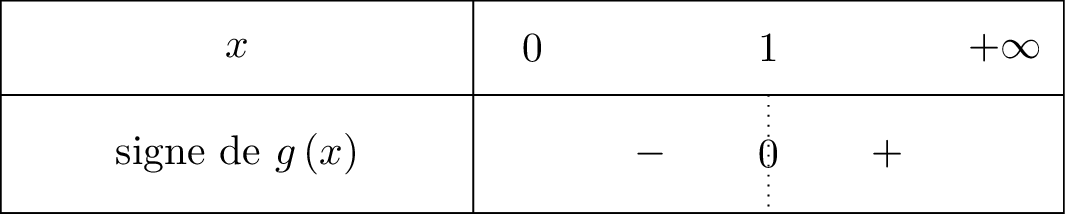
Question 3
Soit la fonction définie sur par . On note la courbe représentative de la fonction .
Montrer que pour tout réel appartenant à on a : .
Correction
Soit la fonction définie sur par .
Nous allons poser la fonction définie sur par : et calculer la dérivée de .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Maintenant nous allons calculer la dérivée de la fonction définie sur par .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Il en résulte donc que :
Nous allons poser la fonction définie sur par : et calculer la dérivée de .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Maintenant nous allons calculer la dérivée de la fonction définie sur par .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Il en résulte donc que :
Question 4
En déduire les variations de sur l'intervalle .
Correction
Nous avons vu que :
Pour tout réel appartenant à l'intervalle , nous connaissons le signe de d'après la question et nous savons également que .
Nous allons traduire toutes ces informations à l'aide d'un tableau de variation :
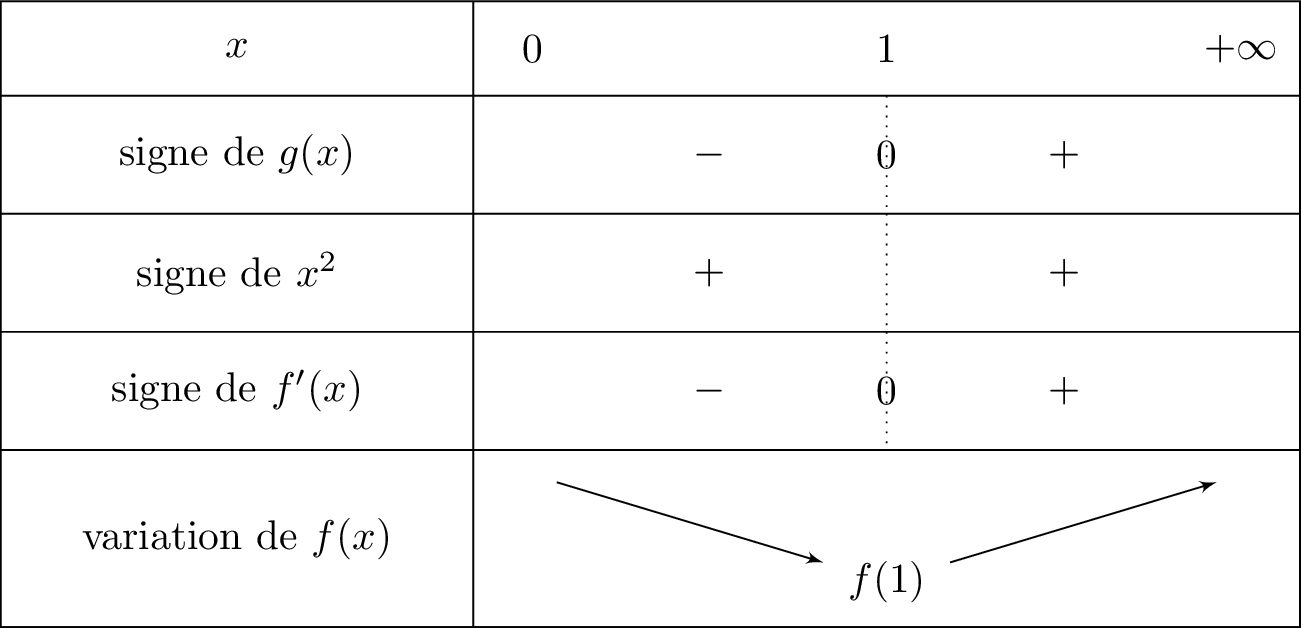
Pour tout réel appartenant à l'intervalle , nous connaissons le signe de d'après la question et nous savons également que .
Nous allons traduire toutes ces informations à l'aide d'un tableau de variation :
