La fonction logarithme
Exercices types : ère partie - Exercice 2
20 min
35
Question 1
Soit la fonction définie sur par . On note la courbe représentative de la fonction .
Calculer .
Correction
est dérivable sur .
Ici on reconnaît la forme : avec ; et
Ainsi : ; et .
Il vient alors que :
équivaut successivement à :
Ici on reconnaît la forme : avec ; et
Ainsi : ; et .
Il vient alors que :
équivaut successivement à :
Question 2
Démontrer que la fonction admet un maximum sur l'intervalle .
Calculer la valeur exacte du maximum de la fonction sur ce même intervalle.
Calculer la valeur exacte du maximum de la fonction sur ce même intervalle.
Correction
Sur l'intervalle , on a : .
Etudions le signe de .
équivaut successivement à :
Cela signifie que dès que et que dès que .
De plus :
Nous traduisons maintenant toutes ces informations dans un tableau de variation.
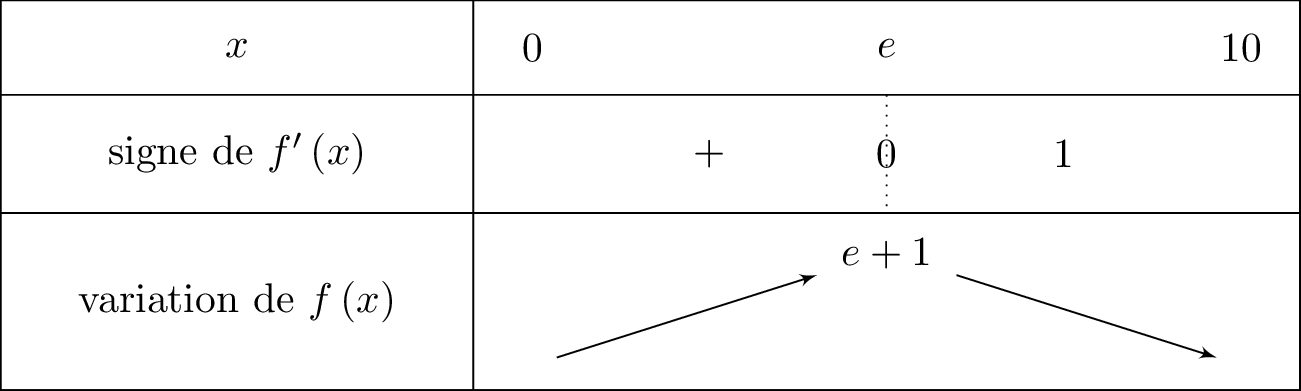
Etudions le signe de .
équivaut successivement à :
Cela signifie que dès que et que dès que .
De plus :
Nous traduisons maintenant toutes ces informations dans un tableau de variation.

Question 3
Montrer que la courbe est entièrement située en dessous de chacune de ses tangentes sur l’intervalle .
Correction
La courbe est entièrement située en dessous de chacune de ses tangentes sur l’intervalle signifie que est concave sur l’intervalle .
Pour étudier la convexité de la fonction , il faut étudier le signe de .
Sur l'intervalle , on sait que : .
Il vient alors que :
. Comme appartient à l'intervalle alors dès que . On en déduit le tableau suivant :
Pour étudier la convexité de la fonction , il faut étudier le signe de .
- Lorsque sur un intervalle alors est convexe et est située au-dessus de ses tangentes.
- Lorsque sur un intervalle alors est concave et est située en dessous de ses tangentes.
Il vient alors que :
. Comme appartient à l'intervalle alors dès que . On en déduit le tableau suivant :
Question 4
On admet que la fonction définie par
est une primitive de la fonction sur l’intervalle .
est une primitive de la fonction sur l’intervalle .
Calculer la valeur exacte de
Correction
Comment calculer l'intégrale ?
1ère étape : on calcule une primitive de notée .
2ème étape : et on effectue le calcul numérique.
équivaut successivement à :1ère étape : on calcule une primitive de notée .
2ème étape : et on effectue le calcul numérique.
Finalement :