La fonction logarithme
Etudes de fonctions - Exercice 3
15 min
25
Question 1
Une entreprise fabrique des protections pour téléphone. On a modélisé le bénéfice mensuel, en milliers d'euros, par la fonction définie sur l'intervalle par où désigne le nombre de protections fabriquées et vendues, en milliers.
Calculer la dérivée, notée , de la fonction .
Correction
est dérivable sur .
Ici on reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
équivaut successivement à :
Ici on reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
équivaut successivement à :
Question 2
Déterminer le tableau de variation complet de la fonction .
Correction
Il nous faut maintenant étudier le signe de .
Pour tout réel , on vérifie aisément que . Donc le signe de dépend de .
Ainsi :
équivaut successivement à :
.
De plus :
d'où :
d'où : et enfin
Nous allons maintenant dresser le tableau de variation de .
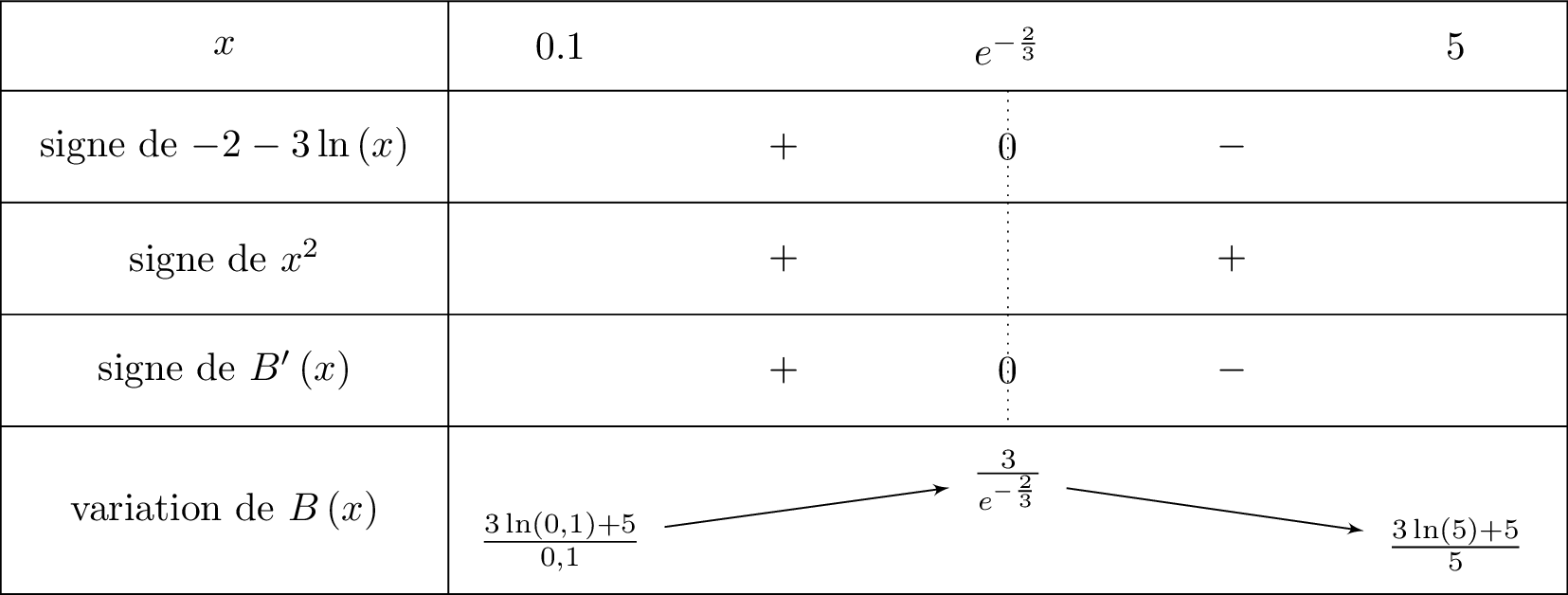
Pour tout réel , on vérifie aisément que . Donc le signe de dépend de .
Ainsi :
équivaut successivement à :
.
De plus :
d'où :
d'où : et enfin
Nous allons maintenant dresser le tableau de variation de .

Question 3
En déduire pour quel nombre de protections fabriquées et vendues le bénéfice est maximal et la valeur de ce bénéfice maximale arrondie à l'euro près.
Correction
D'après le tableau de variation de la question précédente, que l'on redonne ci-dessous :

Le maximum est atteint en et vaut
Or :
.
Le bénéfice est maximal pour une production de protections et la valeur de ce bénéfice est de euros.

Le maximum est atteint en et vaut
Or :
.
Le bénéfice est maximal pour une production de protections et la valeur de ce bénéfice est de euros.