La fonction logarithme
Equation et inéquation - Exercice 3
18 min
30
Pour chaque question, résoudre l'inéquation sur l'intervalle considéré.
Question 1
;
Correction
équivaut successivement à
Le domaine de définition impose que et l'inéquation est vraie si .
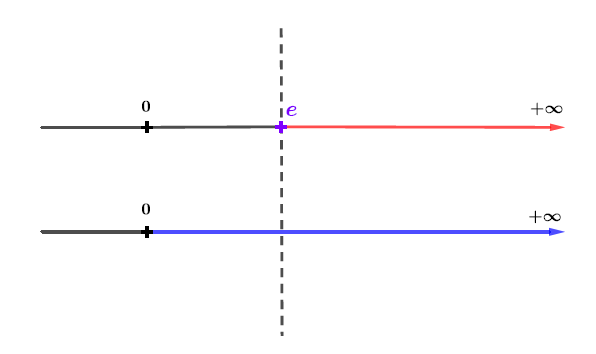
On fait l'intersection des deux intervalles.
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à droite de la barre pointillée verticale.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Le domaine de définition impose que et l'inéquation est vraie si .

On fait l'intersection des deux intervalles.
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à droite de la barre pointillée verticale.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 2
;
Correction
équivaut successivement à :
Le domaine de définition impose que et l'inéquation est vraie si .
On fait l'intersection des deux intervalles.
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à gauche de la barre pointillée verticale.
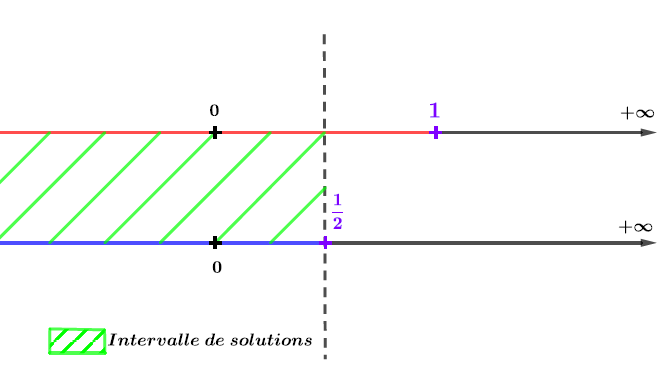
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Le domaine de définition impose que et l'inéquation est vraie si .
On fait l'intersection des deux intervalles.
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone à gauche de la barre pointillée verticale.

Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 3
;
Correction
équivaut successivement à :
Le domaine de définition impose que et l'inéquation est vraie si .
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Le domaine de définition impose que et l'inéquation est vraie si .
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 4
;
Correction
équivaut successivement à :
Pour résoudre l'inéquation , on utilise le discriminant.
; et
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si .
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Pour résoudre l'inéquation , on utilise le discriminant.
; et
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si .
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 5
;
Correction
équivaut successivement à :
Pour résoudre l'inéquation , on utilise le discriminant.
; et
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Pour résoudre l'inéquation , on utilise le discriminant.
; et
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Question 6
;
Correction
équivaut successivement à :
Pour résoudre l'inéquation , on utilise le discriminant.
; et
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :
Pour résoudre l'inéquation , on utilise le discriminant.
; et
L'inéquation est vraie si .
Le domaine de définition impose que et l'inéquation est vraie si
On effectue l'intersection de ces deux ensembles.
Il en résulte que les solutions de l'inéquation sont sur l'intervalle :