La fonction exponentielle
Exercices types : ème partie - Exercice 2
45 min
70
On considère la fonction définie et dérivable sur dont la courbe représentative est donnée ci-dessous.
Le point de coordonnées est l’unique point d’inflexion de la courbe sur l’intervalle . La droite est la tangente à la courbe au point . La courbe admet une tangente horizontale au point d’abscisse . 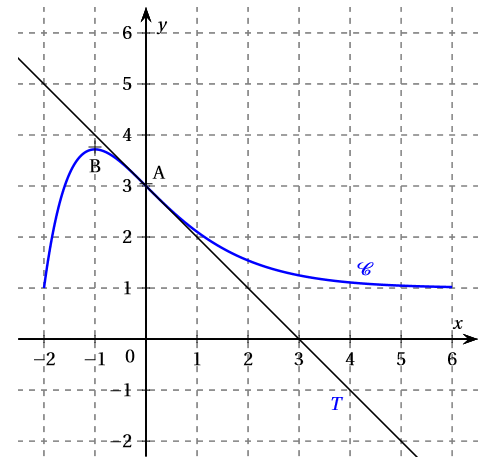

Question 1
Partie A
En utilisant le graphique, répondre aux questions suivantes :
En utilisant le graphique, répondre aux questions suivantes :
Déterminer .
Correction

Question 2
Déterminer . En déduire une équation de la tangente à la courbe au point .
Correction

De plus, le point appartient à cette tangente. Nous allons appelé ce point
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
La tangente admet donc un coefficient directeur qui vaut et l'ordonnée à l'origine vaut .
Une équation de la tangente à la courbe au point est alors :
Question 3
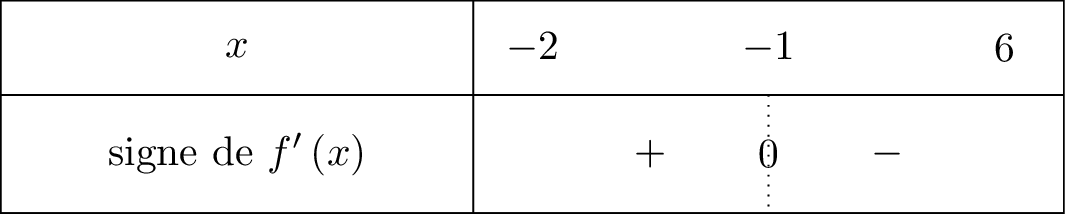
Déterminer le signe de sur .
Correction

- Si est décroissante sur alors est négative sur
- Si est croissante sur alors est positive sur
Question 4
Donner la convexité de sur .
Correction
- Lorsque les tangentes sont situées au-dessus de la courbe sur un intervalle alors est concave sur .
- Lorsque les tangentes sont situées en dessous de la courbe sur un intervalle alors est convexe sur .
- On peut également dire que :
- Lorsque la courbe est située en dessous de ses tangentes sur un intervalle alors est concave sur .
- Lorsque la courbe est située au-dessus de ses tangentes sur un intervalle alors est convexe sur .


Question 5
Donner un encadrement par deux entiers consécutifs de .
Correction
La fonction est positive sur donc l'intégrale est positive et est égale à l'aire du domaine hachuré sur la figure ci-dessous.
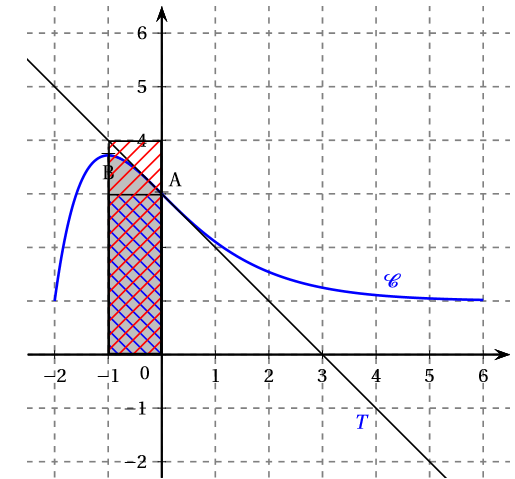 On compte le nombre de carreau sous la courbe et l'axe des abscisses délimité par les droites verticales et .
On compte le nombre de carreau sous la courbe et l'axe des abscisses délimité par les droites verticales et .
On dénombre qu'il y a trois carreaux pleins hachurés et un quatrième pas complet.
Il en résulte donc que :

On dénombre qu'il y a trois carreaux pleins hachurés et un quatrième pas complet.
Il en résulte donc que :
Question 6
Partie B
La fonction est définie par pour tout
La fonction est définie par pour tout
Déterminer la valeur exacte de puis en donner la valeur arrondie au centième.
Correction
Nous savons que .
Ainsi :
équivaut successivement à :
qui correspond à la valeur exacte. qui correspond à la valeur arrondie au centième.
Ainsi :
équivaut successivement à :
Question 7
Montrer que, pour tout , on a : .
Correction
Soit :
Ainsi : ; et .
Il vient alors que :
. On factorise par .
D'où :
Ici on reconnaît la forme : avec ; et .
Ainsi : ; et .
Il vient alors que :
. On factorise par .
D'où :
Question 8
Étudier le signe de sur puis donner le tableau de variation de sur .
Correction
Nous venons de démontrer que :
Pour tout réel , on a : .
De plus,
équivaut successivement à :
.
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :
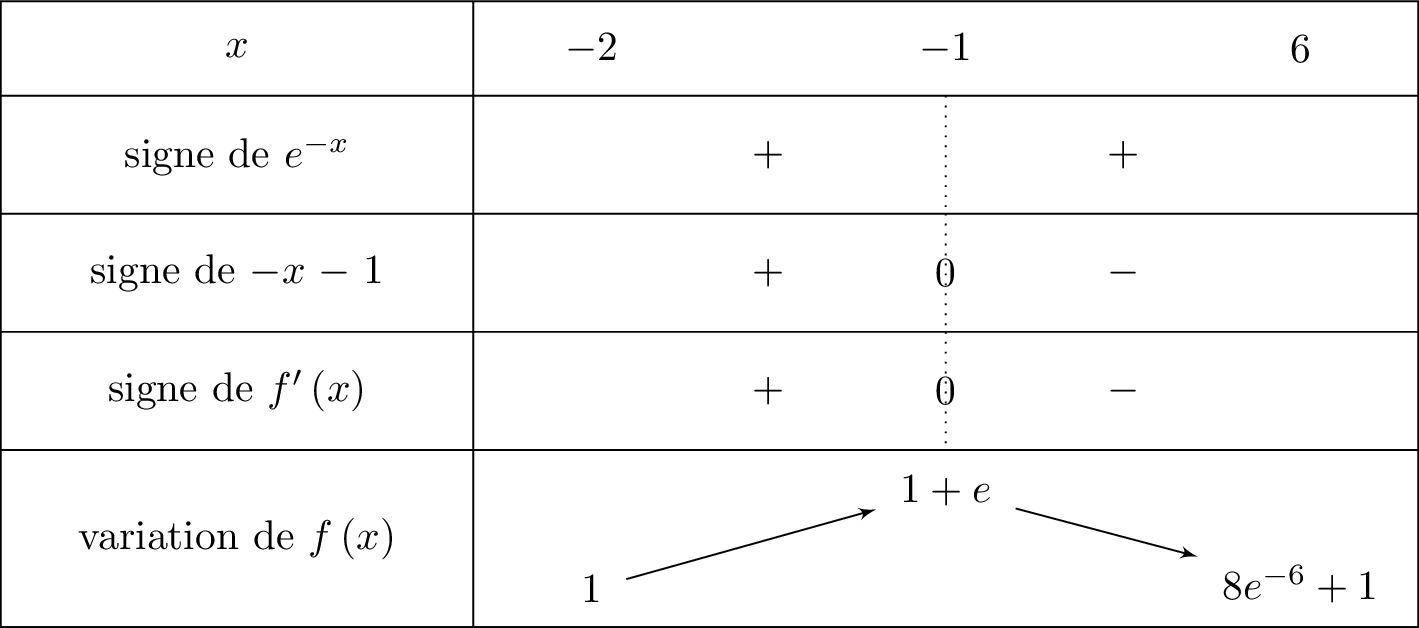
d'où d'où
Pour tout réel , on a : .
De plus,
équivaut successivement à :
.
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :

Question 9
Un logiciel de calcul formel donne l’information suivante :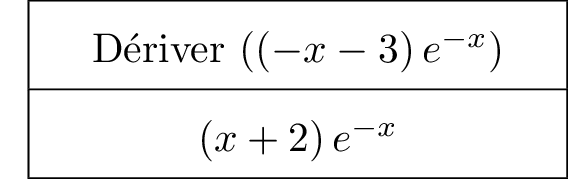
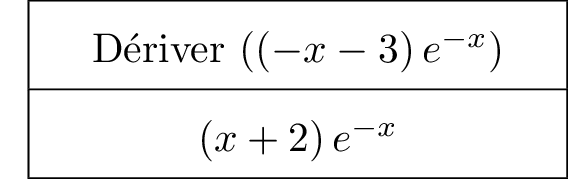
Déterminer une primitive de sur .
Correction
D'après le logiciel formel, nous pouvons voir qu'une primitive de la fonction est car lorsque nous dérivons nous obtenons .
Nous savons que alors une primitive de est alors :
Nous savons que alors une primitive de est alors :
Question 10
Calculer la valeur moyenne de sur . On donnera sa valeur exacte puis sa valeur arrondie au dixième.
Correction
une fonction continue sur un intervalle .
La valeur moyenne de la fonction sur est le réel défini par
On a : La valeur moyenne de la fonction sur est le réel défini par
équivaut successivement à :
: Valeur exacte .
: Valeur arrondie au dixième.