La fonction exponentielle

Exercices types : 22ème partie - Exercice 4

45 min
70
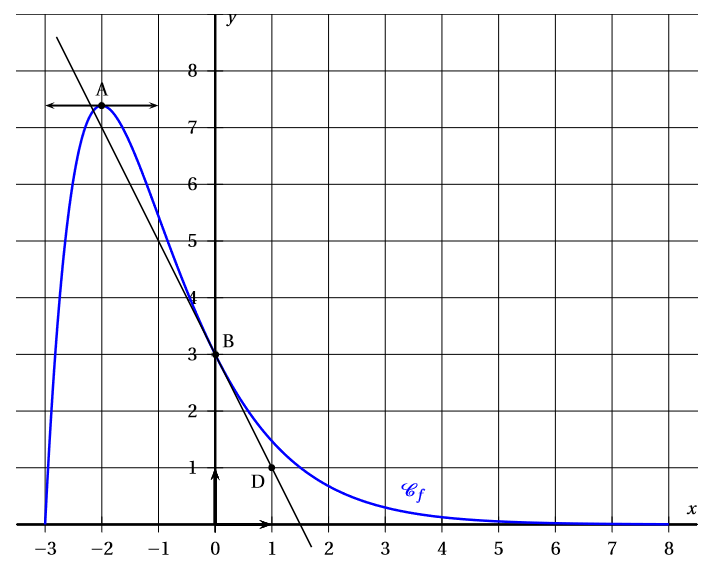
Dans le repère orthonormé ci-dessous, on a tracé la courbe représentative CfC_{f} d’une fonction ff définie et dérivable sur l’intervalle [−3;8]\left[-3;8\right]. On note f′f' sa dérivée.
  • AA est le point de CfC_{f} d’abscisse −2-2.
  • BB est le point de CfC_{f} de coordonnées (0;3)\left(0;3\right)
  • La tangente à CfC_{f} au point AA est horizontale.
  • La droite TT est la tangente à CfC_{f} au point BB d’abscisse 00 et elle passe parle point D(1;1)D\left(1; 1\right).
Question 1

Donner la valeur de f′(−2)f'\left(-2\right).

Correction
Au point d'abscisse −2-2, la tangente à la courbe CfC_{f} est horizontale. Il en résulte donc que :
f′(−2)=0f'\left(-2\right)=0

Question 2

Interpréter géométriquement f′(0)f'\left(0\right) et donner sa valeur.

Correction
f′(0)f'\left(0\right) est le coefficient directeur de la tangente en BB à la courbe CfC_{f} . Cette tangente est la droite (BD)\left(BD\right) donc a pour coefficient directeur :
f′(0)=yD−yBxD−xBf'\left(0\right)=\frac{y_{D} -y_{B} }{x_{D} -x_{B} }
f′(0)=1−31−0f'\left(0\right)=\frac{1-3}{1-0}
f′(0)=−2f'\left(0\right)=-2
Question 3

La fonction ff est-elle convexe sur [−2;2]\left[-2;2\right].

Correction
  • Lorsque les tangentes sont situées au-dessus de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est concave sur [a,b]\left[a,b\right].
  • Lorsque les tangentes sont situées en dessous de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est convexe sur [a,b]\left[a,b\right].
Au point d'abscisse x=−2x =-2 la tangente est au dessus de la courbe CfC_{f} donc la fonction ff est concave. Ainsi ff n’est pas convexe sur [−2;2]\left[-2;2\right].
Question 4
Partie B : On admet désormais que la fonction ff de la partie AA est définie sur l’intervalle [−3;8]\left[-3 ; 8\right] par f(x)=(x+3)e−xf\left(x\right)=\left(x+3\right)e^{-x}.
Un logiciel de calcul formel donne les résultats suivants :

Étudier le signe de la dérivée de la fonction ff.

Correction
D’après le logiciel de calcul formel, nous pouvons lire que : f′(x)=(−x−2)e−xf'\left(x\right)=\left(-x-2\right)e^{-x}
Pour tout réel x∈[−3;8]x\in\left[-3 ; 8\right], on vérifie aisément que e−x>0e^{-x}>0, donc le signe de f′f' dépend de −x−2-x-2.
Or :
−x−2≥0-x-2\ge0 équivaut successivement à :
−x≥2-x\ge2
x≤−2x\le-2
Il en résulte donc que :
  • si x∈[−3;−2]x\in\left[-3 ; -2\right] alors f′(x)≥0f'\left(x\right)\ge0
  • si x∈[−2;8]x\in\left[-2 ; 8\right] alors f′(x)≤0f'\left(x\right)\le0
Question 5

Dresser le tableau de variation de la fonction ff sur l’intervalle [−3;8]\left[-3 ; 8\right].

Correction
Nous traduisons les infirmations de la question 44, dans le tableau de variation ci-dessous :

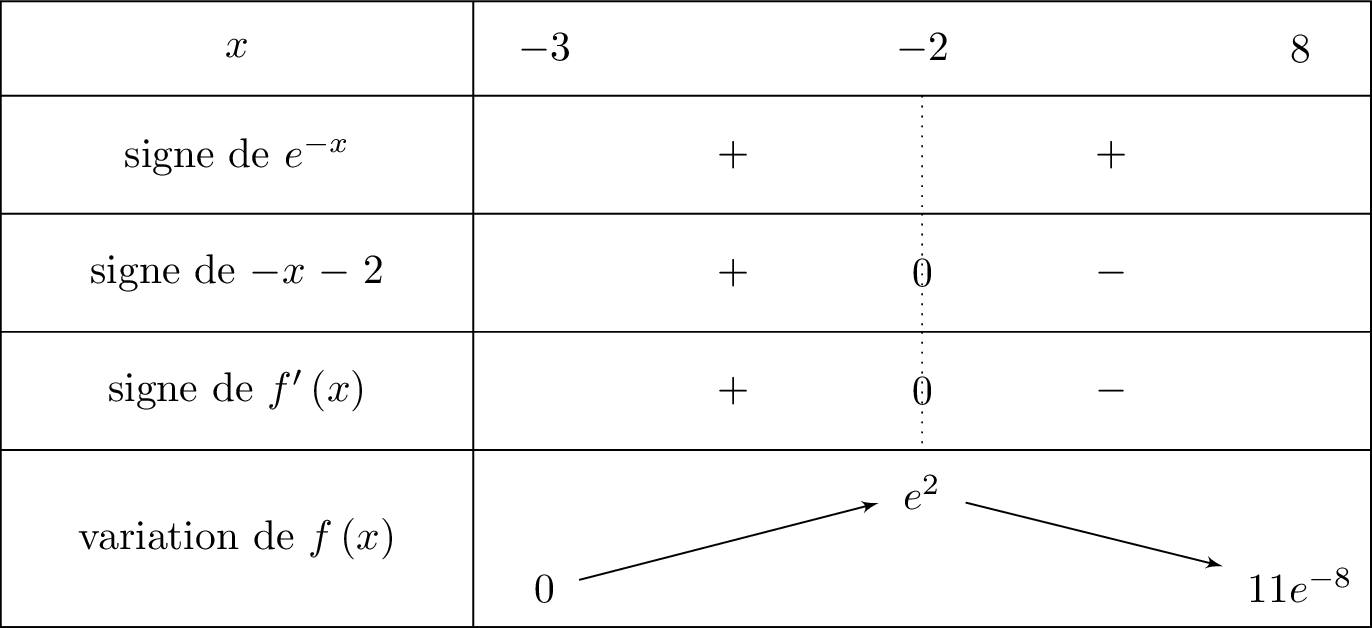
De plus :
  • f(−3)=(−3+3)e3f\left(-3\right)=\left(-3+3\right)e^{3} donc f(−3)=0f\left(-3\right)=0
  • f(−2)=(−2+3)e2f\left(-2\right)=\left(-2+3\right)e^{2} donc f(−2)=e2f\left(-2\right)=e^{2}
  • f(8)=(8+3)e−8f\left(8\right)=\left(8+3\right)e^{-8} donc f(8)=11e−8f\left(8\right)=11e^{-8}
Question 6

Montrer que l’équation f(x)=3f\left(x\right)=3 admet une unique solution α\alpha sur [−3;−2]\left[-3 ; -2\right].

Correction
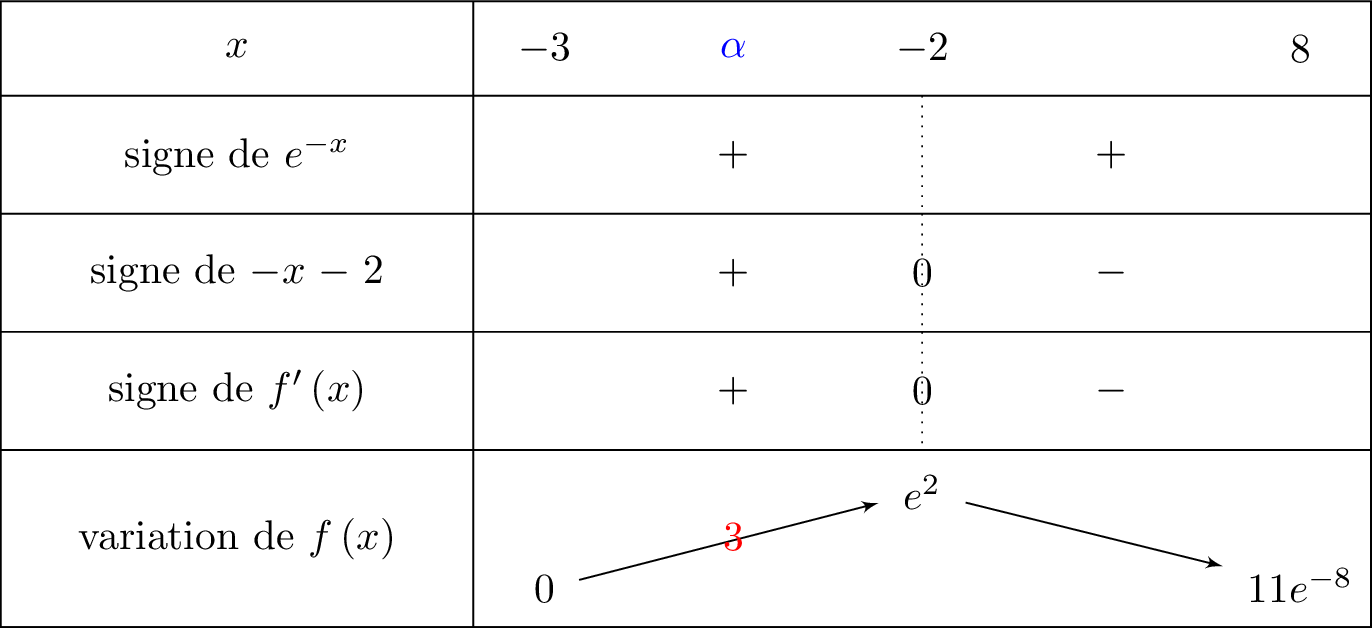
  • Sur [−3;−2]\left[-3 ;-2\right], la fonction ff est continue et strictement croissante.
    De plus, f(−3)=0<3f\left(-3\right)=0<3 et f(−2)=e2>3f\left(-2\right)=e^{2}>3 .
    Or 3∈[0;e2]3\in \left[0;e^{2}\right], donc d'après le théorème des valeurs intermédiaires, il existe une unique solution α\alpha dans [−3;−2]\left[-3;-2\right] tel que f(x)=3f\left(x\right)=3.
Question 7

Donner une valeur approchée de α\alpha à 0,010,01 près.

Correction
A la calculatrice, on vérifie que :
f(−2,83)≈2,88f\left(-2,83\right)\approx 2,88 et f(−2,82)≈3,02f\left(-2,82\right)\approx 3,02 . Or 3∈]2,88;3,02]3\in \left]2,88;3,02\right], donc d'après le théorème des valeurs intermédiaires on en déduit que :
−2,83≤α≤−2,82-2,83\le \alpha \le -2,82
Question 8

Justifier que la fonction FF définie sur l’intervalle [−3;8]\left[-3 ; 8\right] par F(x)=(−x−4)e−xF\left(x\right)=\left(-x-4\right)e^{-x} est une primitive de ff sur le même intervalle.

Correction
Dans le cas où une primitive FF est donnée, il vous suffit de dériver FF et d'obtenir comme résultat ff.
Autrement dit, il faut que F′(x)=f(x)F'\left(x\right)=f\left(x\right)
Soit : F(x)=(−x−4)e−xF\left(x\right)=\left(-x-4\right)e^{-x} . FF est dérivable sur [−3;8]\left[-3 ; 8\right].
On reconnaît la forme : (uv)′=u′v+uv′\left(uv\right)'=u'v+uv' avec u(x)=−x−4u\left(x\right)=-x-4 et v(x)=e−xv\left(x\right)=e^{-x} .
Ainsi : u′(x)=−1u'\left(x\right)=-1 et v′(x)=−e−xv'\left(x\right)=-e^{-x} .
Il vient alors que :
F′(x)=−1×e−x+(−x−4)×(−e−x)F'\left(x\right)=-1\times e^{-x} +\left(-x-4\right)\times \left(-e^{-x} \right)
F′(x)=−1×e−x+(−x)×(−e−x)+(−4)×(−e−x)F'\left(x\right)=-1\times e^{-x} +\left(-x\right)\times \left(-e^{-x} \right)+\left(-4\right)\times \left(-e^{-x} \right)
F′(x)=−e−x+xe−x+4e−xF'\left(x\right)=-e^{-x} +xe^{-x} +4e^{-x}
F′(x)=3e−x+xe−xF'\left(x\right)=3e^{-x} +xe^{-x}
F′(x)=e−x(3+x)F'\left(x\right)=e^{-x} \left(3+x\right)
F′(x)=f(x)F'\left(x\right)=f\left(x\right)

Donc FF définie sur l’intervalle [−3;8]\left[-3 ; 8\right] par F(x)=(−x−4)e−xF\left(x\right)=\left(-x-4\right)e^{-x} est bien une primitive de ff.
Question 9

Calculer la valeur exacte de l’aire, du domaine délimité par les droites d’équation x=0x=0, x=3x=3, l’axe des abscisses et la courbe CfC_{f} .

Correction
Comment calculer l'intégrale I=∫abf(x)dxI=\int _{a}^{b}f\left(x\right) dx ?
1ère étape : on calcule une primitive de ff notée FF.
2ème étape : I=F(b)−F(a)I=F\left(b\right)-F\left(a\right) et on effectue le calcul numérique.
L'énoncé de la question revient à effectuer le calcul de : ∫03f(x)dx\int _{0}^{3}f\left(x\right) dx
Soit f(x)=e−x(3+x)f\left(x\right)=e^{-x} \left(3+x\right) alors F(x)=(−x−4)e−xF\left(x\right)=\left(-x-4\right)e^{-x}
Il vient alors que :
∫03f(x)dx=F(3)−F(0)\int _{0}^{3}f\left(x\right) dx=F\left(3\right)-F\left(0\right) équivaut successivement à :
∫03f(x)dx=((−3−4)e−3)−((−0−4)e−0)\int _{0}^{3}f\left(x\right) dx=\left(\left(-3-4\right)e^{-3} \right)-\left(\left(-0-4\right)e^{-0} \right)
∫03f(x)dx=(−7e−3)+4\int _{0}^{3}f\left(x\right) dx=\left(-7e^{-3} \right)+4
Finalement :
∫03f(x)dx=4−7e−3\int _{0}^{3}f\left(x\right) dx=4-7e^{-3}
Question 10

Calculer la valeur moyenne de ff sur [0;3]\left[0;3\right]. Donner la valeur exacte. Puis un arrondi à 10−210^{-2} près.

Correction
ff une fonction continue sur un intervalle [a;b]\left[a;b\right].
La valeur moyenne de la fonction ff sur [a;b]\left[a;b\right] est le réel mm défini par m=1b−a∫abf(x)dxm=\frac{1}{b-a} \int _{a}^{b}f\left(x\right) dx
Dans notre situation, nous avons donc :
m=13−0∫03f(x)dxm=\frac{1}{3-0} \int _{0}^{3}f\left(x\right) dx
Ainsi :
m=13×(4−7e−3)dxm=\frac{1}{3} \times\left(4-7e^{-3}\right) dx
qui correspond à la valeur exacte.
m≈1,22m\approx1,22
qui correspond à un arrondi à 10−210^{-2} près.