La fonction exponentielle
Exercices types : ère partie - Exercice 4
40 min
65
PARTIE A.
On considère la fonction définie et dérivable sur l’intervalle par .
Un logiciel de calcul formel fournit les résultats suivants que l’on pourra utiliser :
On considère la fonction définie et dérivable sur l’intervalle par .
Un logiciel de calcul formel fournit les résultats suivants que l’on pourra utiliser :
Question 1
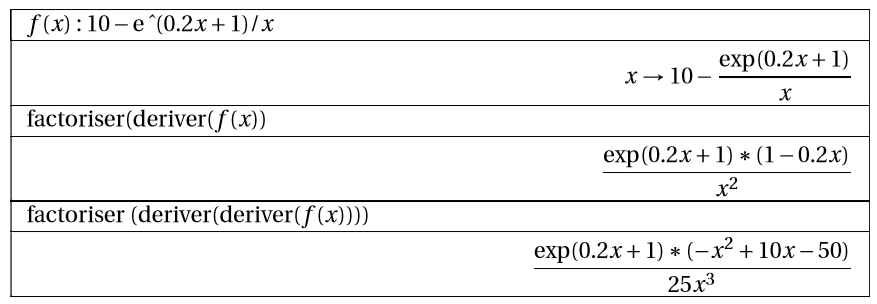
Retrouver par le calcul l’expression factorisée de où est la fonction dérivée de .
Correction
est dérivable sur l’intervalle .
On reconnaît la forme avec et
Ainsi : ; et .
Il vient alors que :
. Comme nous avons le signe moins devant la fraction , nous allons multiplier le numérateur par
Il en résulte donc que :
On reconnaît la forme avec et
Ainsi : ; et .
Il vient alors que :
. Comme nous avons le signe moins devant la fraction , nous allons multiplier le numérateur par
Il en résulte donc que :
Question 2
Étudier le signe de sur l’intervalle et dresser le tableau de variation de sur l’intervalle . On arrondira les valeurs au millième.
Correction
Pour tout réel appartenant à l'intervalle , on vérifie aisément que et . Il en résulte que le signe de dépend alors de .
Résolvons alors :
Cela signifie donc que lorsque et que lorsque .
Nous allons traduire cela dans un tableau de variation :
 De plus :
De plus :
Résolvons alors :
Cela signifie donc que lorsque et que lorsque .
Nous allons traduire cela dans un tableau de variation :

Question 3
Démontrez que l'équation admet une unique solution .
Donnez un encadrement de à près.
Donnez un encadrement de à près.
Correction
On reprend le tableau de variation fait à la question . On fera apparaître dans le tableau la valeur deux que l'on recherche.
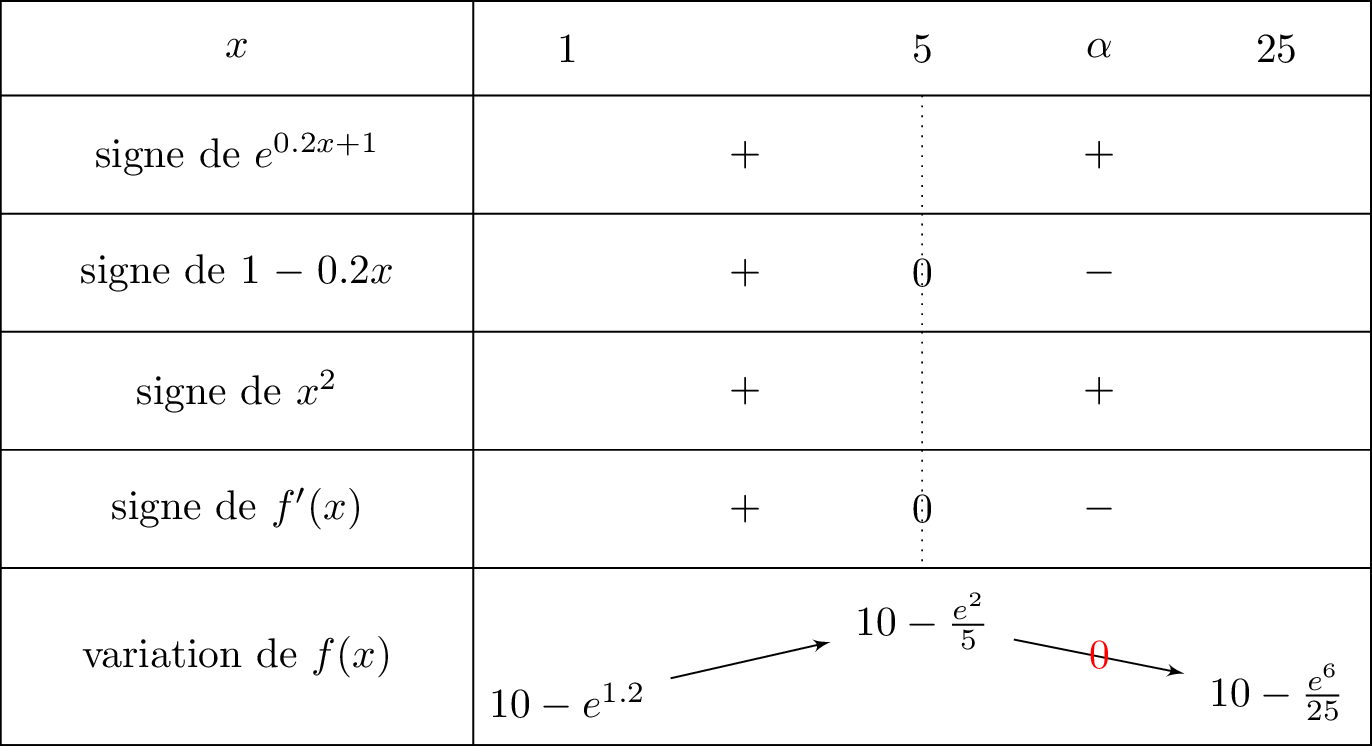 Sur , la fonction est continue et admet comme minimum.
Sur , la fonction est continue et admet comme minimum.
La fonction est strictement positive sur cet intervalle.
Donc l'équation n'a pas de solution sur cet intervalle.
Sur , la fonction est continue et strictement décroissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
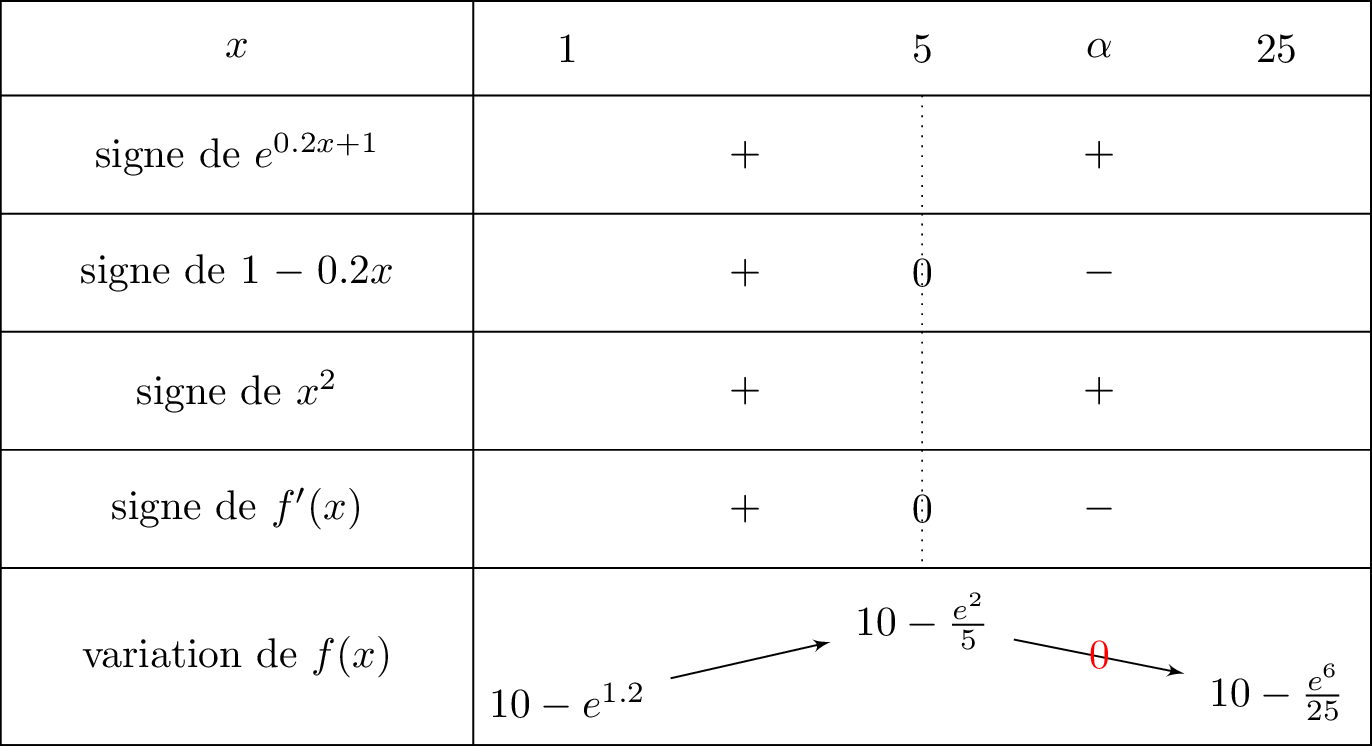
La fonction est strictement positive sur cet intervalle.
Donc l'équation n'a pas de solution sur cet intervalle.
Sur , la fonction est continue et strictement décroissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 4
En utilisant un des résultats donnés par le logiciel de calcul formel, justifier que la fonction est concave sur l’intervalle .
Correction
Le logiciel de calcul formel nous donne la dérivée seconde de . Ainsi :
Pour tout réel appartenant à l'intervalle , on vérifie aisément que et . Il en résulte que le signe de dépend alors de .
Pour étudier le signe de on va utiliser le discriminant .
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
. Il n'y a donc pas de racines réelles. Comme , la parabole est tournée vers le bas et ne traverse jamais l'axe des abscisses. Par conséquent, est du signe de .
Il en résulte donc que sur l'intervalle , on a : ce qui signifie que est concave sur cette intervalle.

Pour tout réel appartenant à l'intervalle , on vérifie aisément que et . Il en résulte que le signe de dépend alors de .
Pour étudier le signe de on va utiliser le discriminant .
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
. Il n'y a donc pas de racines réelles. Comme , la parabole est tournée vers le bas et ne traverse jamais l'axe des abscisses. Par conséquent, est du signe de .
Il en résulte donc que sur l'intervalle , on a : ce qui signifie que est concave sur cette intervalle.

Question 5
PARTIE B.
Une société agro-alimentaire fabrique des aliments pour bétail. On s’intéresse au bénéfice réalisé, en millier d’euros, correspondant à la production d’une quantité de dizaines de tonnes d’aliments. On admet que ce bénéfice peut être modélisé par la fonction étudiée dans la partie ci-dessus. La production minimale est de tonnes, ainsi . Les réponses aux questions suivantes seront justifiées grâce à la partie .
Une société agro-alimentaire fabrique des aliments pour bétail. On s’intéresse au bénéfice réalisé, en millier d’euros, correspondant à la production d’une quantité de dizaines de tonnes d’aliments. On admet que ce bénéfice peut être modélisé par la fonction étudiée dans la partie ci-dessus. La production minimale est de tonnes, ainsi . Les réponses aux questions suivantes seront justifiées grâce à la partie .
Quel est le montant en euro du bénéfice maximal que peut dégager la société? Pour quelle quantité d’aliments ce bénéfice maximal est-il obtenu?
Correction
D’après la partie , on a vu que admet un maximum lorsque . La valeur de ce maximum est alors c'est à dire euros.
Le bénéfice maximal est alors de euros pour la production de tonnes.
Le bénéfice maximal est alors de euros pour la production de tonnes.
Question 6
Déterminer, à la tonne près, la quantité maximale d’aliments qu’il faut fabriquer pour que la société réalise un bénéfice.
Correction
On a vu dans la partie que est positive sur l’intervalle et que . La société peut donc fabriquer au maximum tonnes (à une tonne près) d’aliments pour réaliser un bénéfice.