La fonction exponentielle
Exercices types : ère partie - Exercice 2
30 min
50
Question 1
Soit la fonction définie sur par . On note sa courbe représentative.
Etudiez les variations de . Calculer et en déduire le signe de .
Correction
est dérivable sur . On a :
Or :
équivaut successivement à :
. Cela signifie que est positive ou nulle dès que .
De plus , c'est à dire .
Nous allons pouvoir dresser le tableau de variation de . Il vient alors que :
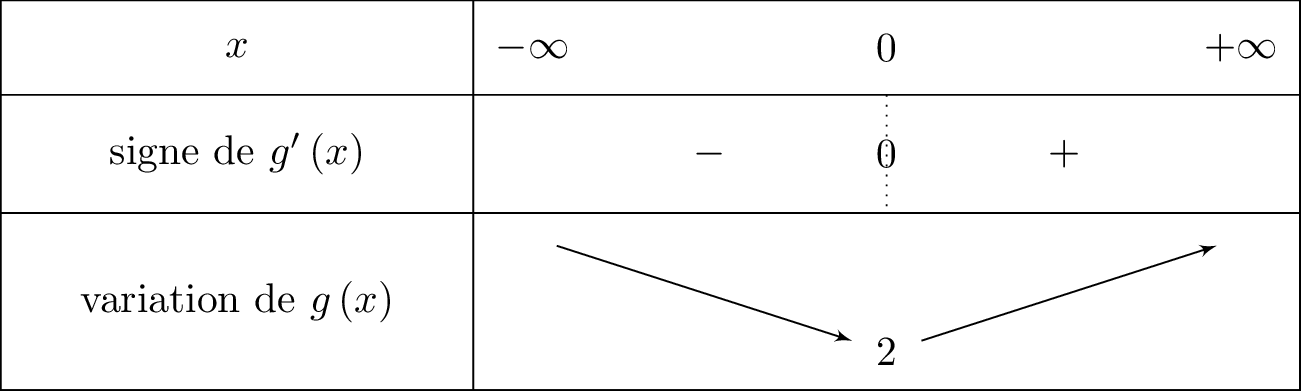 On remarque que le minimum de vaut lorsque . Il en résulte alors que est positive sur ou encore sur .
On remarque que le minimum de vaut lorsque . Il en résulte alors que est positive sur ou encore sur .
On en déduit alors le signe de .
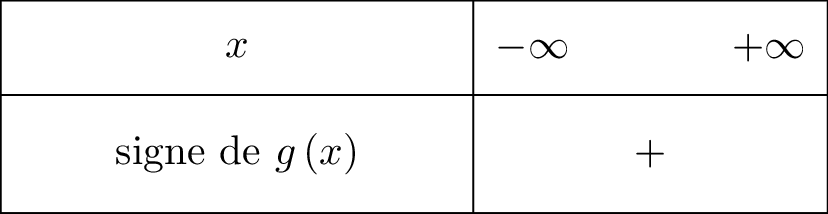
Or :
équivaut successivement à :
. Cela signifie que est positive ou nulle dès que .
De plus , c'est à dire .
Nous allons pouvoir dresser le tableau de variation de . Il vient alors que :

On en déduit alors le signe de .

Question 2
On considère maintenant la fonction définie sur par . On note sa courbe représentative.
Montrer que pour tout réel appartenant à l'intervalle , on a :
Correction
est dérivable sur .
Ici on reconnaît la forme : avec et et .
Ainsi : et et .
Il vient alors que :
. Nous allons tout mettre au même dénominateur.
. Maintenant on factorise par , ce qui donne :
. Puis on simplifie le numérateur et le dénominateur par . D'où :
Ainsi :
Ici on reconnaît la forme : avec et et .
Ainsi : et et .
Il vient alors que :
. Nous allons tout mettre au même dénominateur.
. Maintenant on factorise par , ce qui donne :
. Puis on simplifie le numérateur et le dénominateur par . D'où :
Ainsi :
Question 3
En déduire les variations de la fonction .
Correction
Pour tout réel appartenant à , on a :
Nous savons que , donc le signe de dépend du signe de . Or, d'après la question , pour tout réel appartenant à l'intervalle donc pour tout réel appartenant à l'intervalle . Ainsi pour tout réel appartenant à l'intervalle
Nous avons donc le tableau de variation ci-dessous :
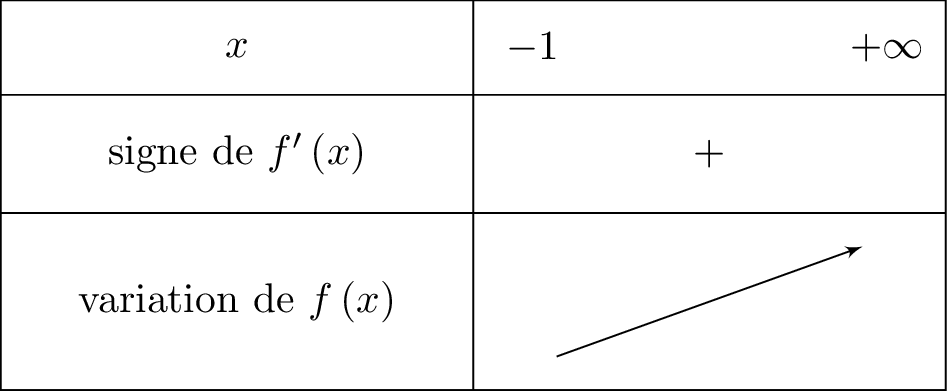
Nous savons que , donc le signe de dépend du signe de . Or, d'après la question , pour tout réel appartenant à l'intervalle donc pour tout réel appartenant à l'intervalle . Ainsi pour tout réel appartenant à l'intervalle
Nous avons donc le tableau de variation ci-dessous :

Question 4
Démontrez que l'équation admet une unique solution .
Donnez un encadrement de à près.
Donnez un encadrement de à près.
Correction
Nous allons reproduire le tableau de variation de uniquement sur l'intervalle .
On a :
et
On a donc le tableau de variation ci-dessous, et l'on a fait également apparaître le zéro que l'on recherche.
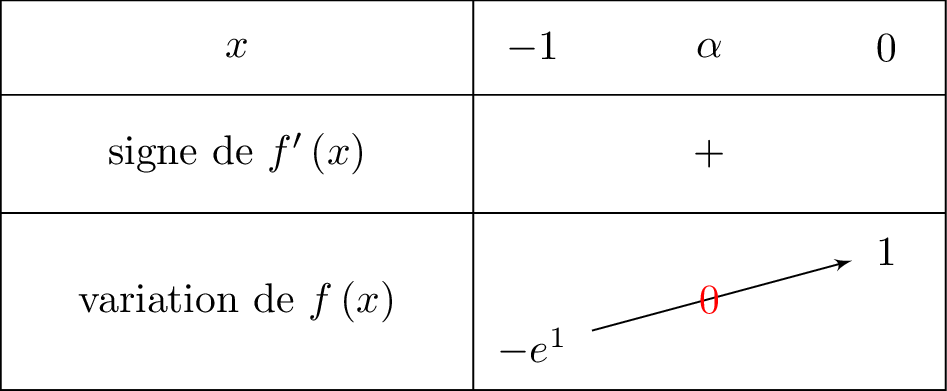
Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
On a :
et
On a donc le tableau de variation ci-dessous, et l'on a fait également apparaître le zéro que l'on recherche.
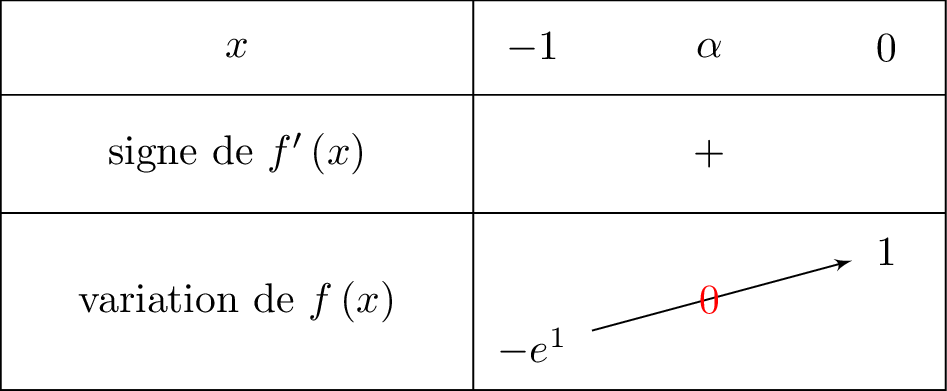
Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 5
En déduire le signe de sur .
Correction
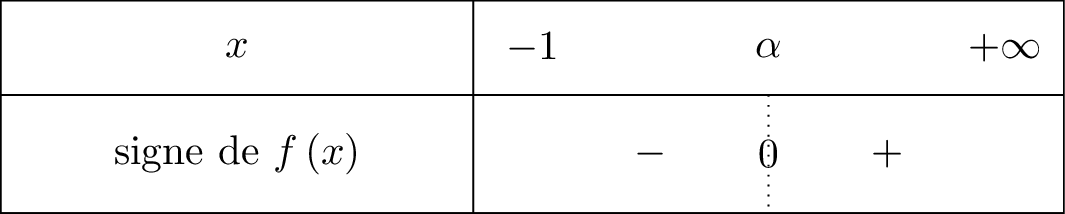
Sur , la fonction est continue et strictement croissante et .
Donc pour tout et pour tout .
On résume cela dans un tableau de signe :
Donc pour tout et pour tout .
On résume cela dans un tableau de signe :
