La fonction exponentielle
Etude de fonctions - Exercice 2
25 min
35
Etudiez les variations des fonctions suivantes
Question 1
Correction
Ici on reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Pour tout réel , on a : .
De plus :
équivaut successivement à :
.
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :
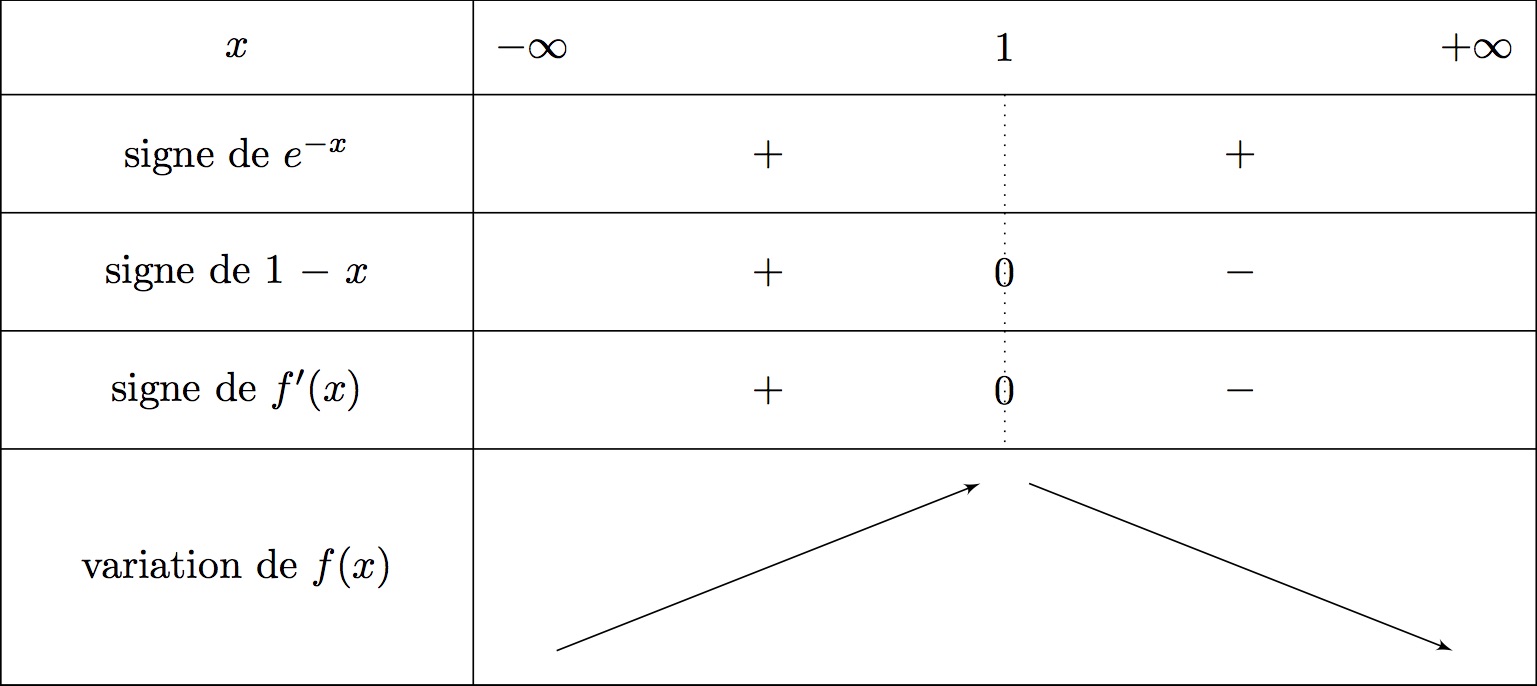
Ainsi : et .
Il vient alors que :
Pour tout réel , on a : .
De plus :
équivaut successivement à :
.
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :

Question 2
Correction
Ici on reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Ainsi :
Pour tout réel , on a : .
De plus,
équivaut successivement à :
.
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :
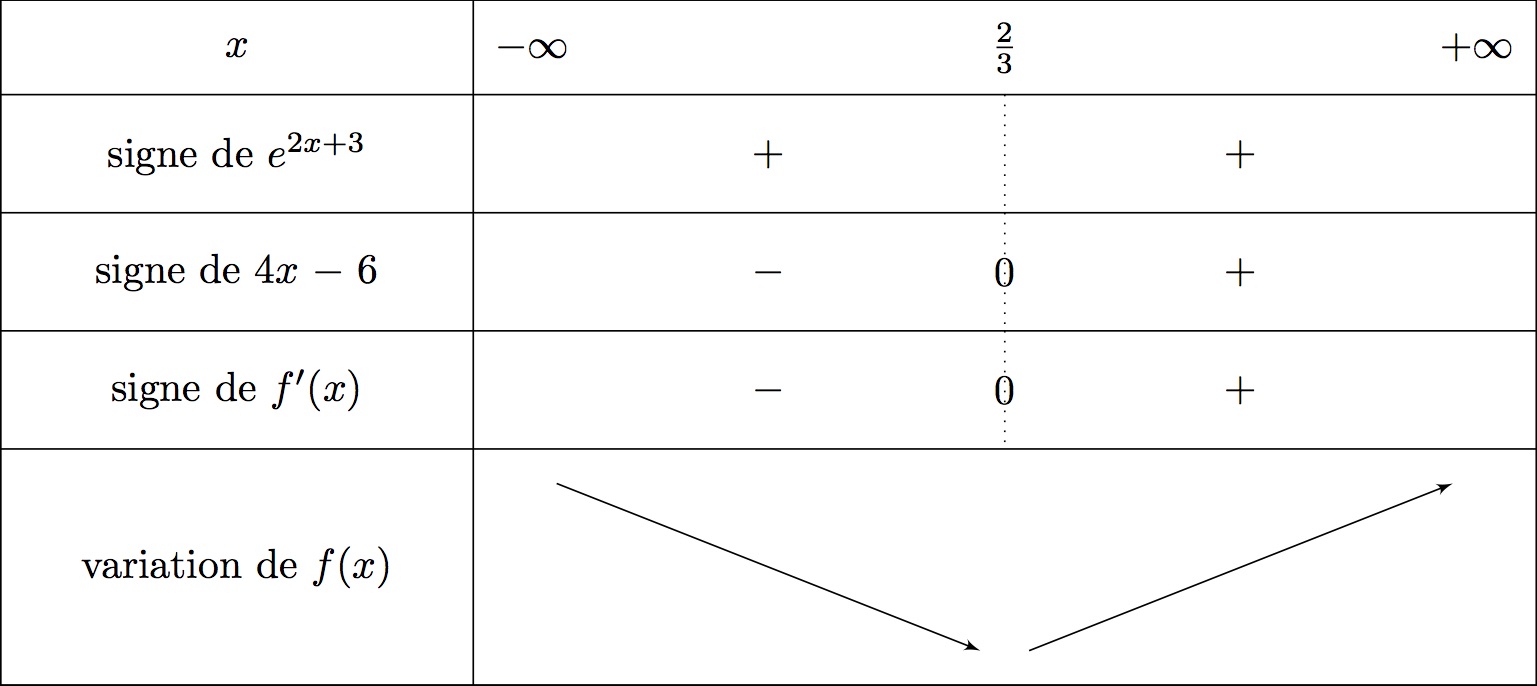
Ainsi : et .
Il vient alors que :
Ainsi :
Pour tout réel , on a : .
De plus,
équivaut successivement à :
.
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :

Question 3
Correction
Ici on reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Ainsi :
Pour tout réel , on a : .
De plus :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :
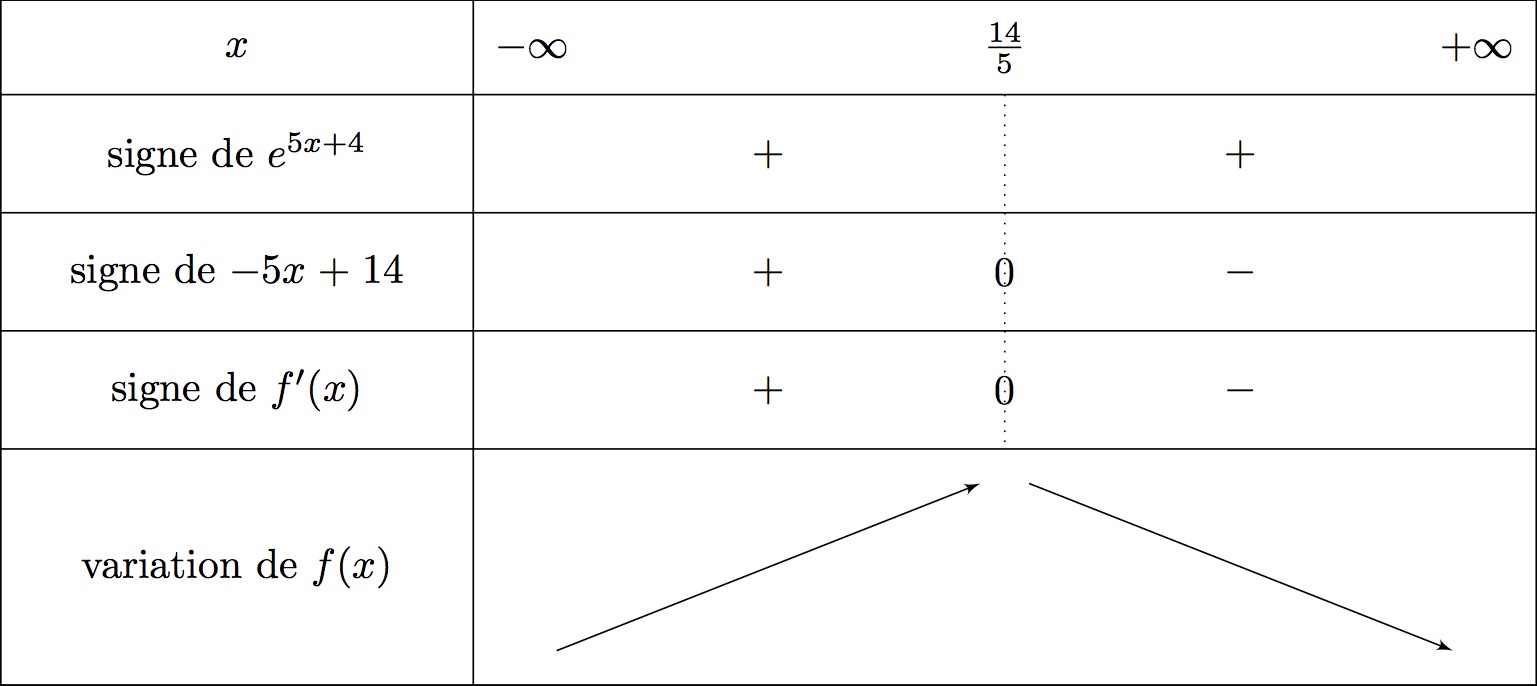
Ainsi : et .
Il vient alors que :
Ainsi :
Pour tout réel , on a : .
De plus :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :

Question 4
Correction
Ici on reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Ainsi :
Pour tout réel , on a .
De plus :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :
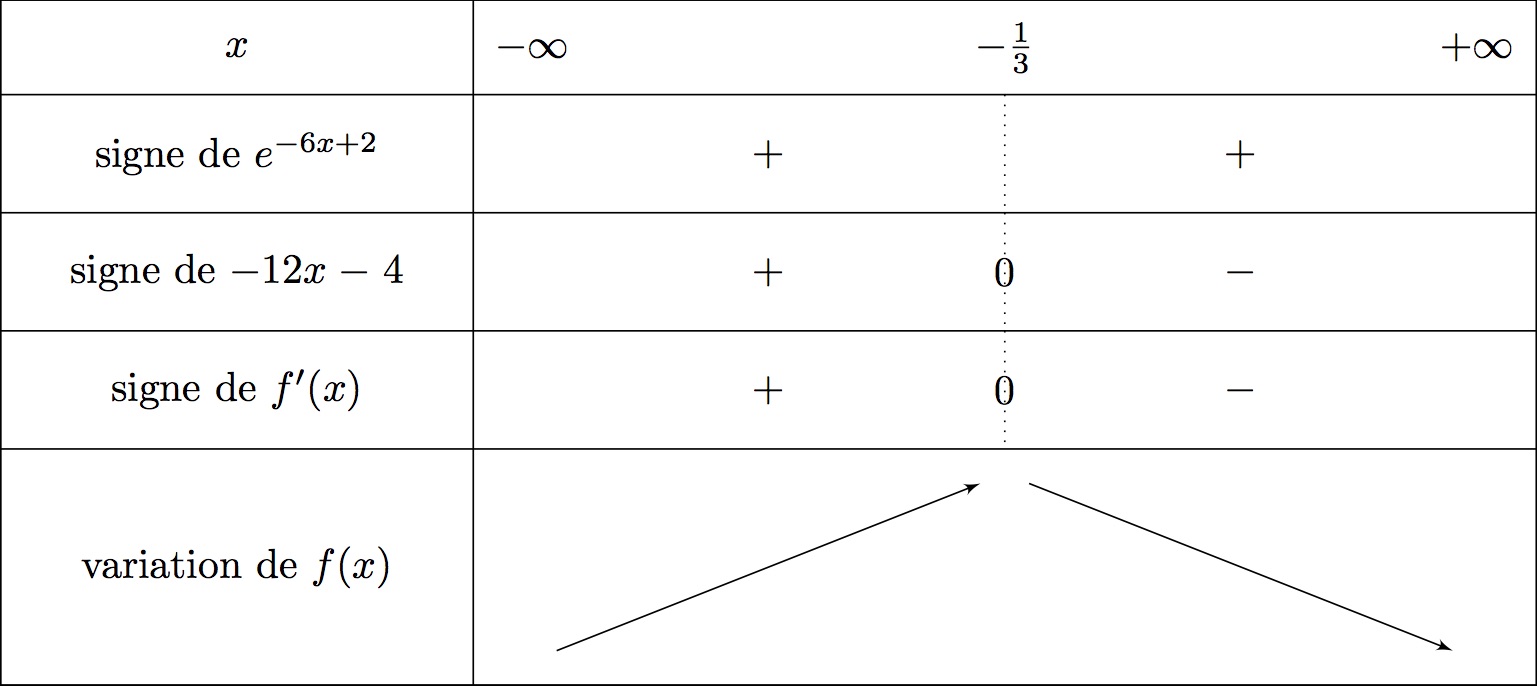
Ainsi : et .
Il vient alors que :
Ainsi :
Pour tout réel , on a .
De plus :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
On en déduit le tableau de variation suivant :

Question 5
Correction
Ici on reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Pour tout réel , on a : .
Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de variation suivant :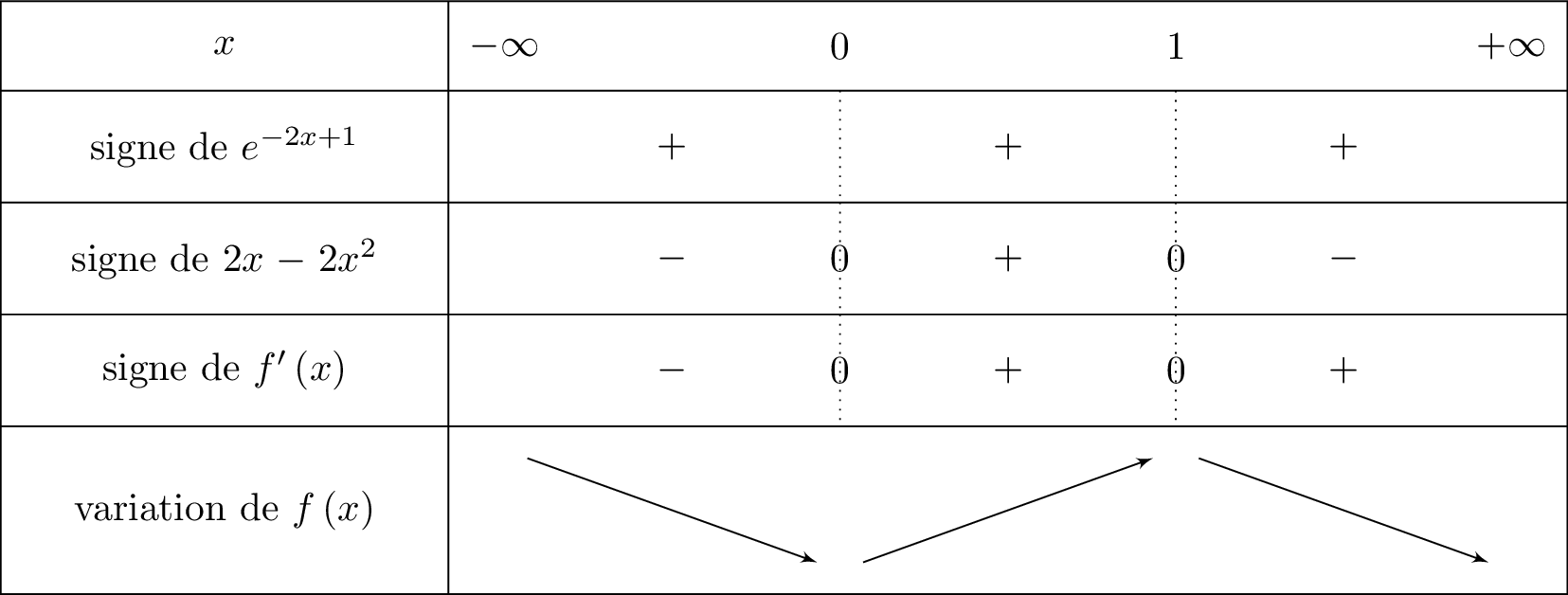
Ainsi : et .
Il vient alors que :
Pour tout réel , on a : .
Pour l'étude de , on va utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et .
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On en déduit le tableau de variation suivant :
