Continuité, dérivation, lectures graphiques et convexité
Exercices types : ème partie - Exercice 4
25 min
40
Question 1
On considère la fonction une fonction définie sur par : et sa courbe représentative dans un repère du plan.
Déterminer le tableau de variation de la fonction sur .
Correction
est dérivable sur .
Il en résulte donc que et de ce fait est strictement croissante sur .
 d'où
d'où
d'où
. Pour tout réel appartenant à l'intervalle , on sait que et de ce fait .
Il en résulte donc que et de ce fait est strictement croissante sur .

d'où
Question 2
Démontrer que l'équation admet une unique solution sur l'intervalle .
On notera cette solution.
On notera cette solution.
Correction
On reprend le tableau de variation fait à la question . On fera apparaître le zéro que l'on recherche. 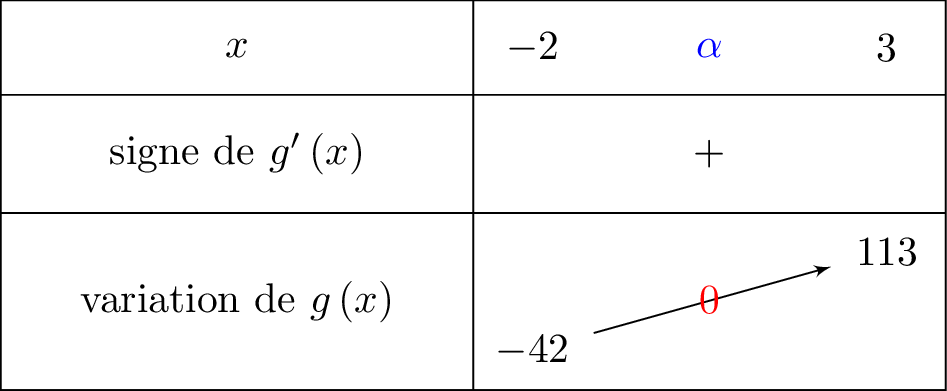
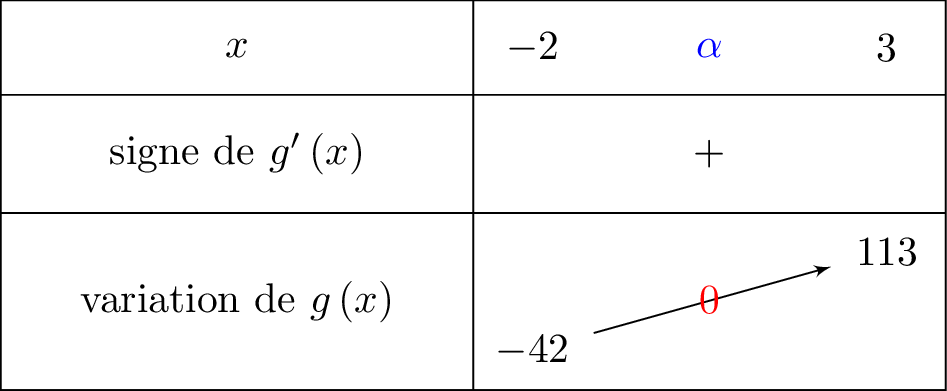
- Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que
Question 3
Déterminer un encadrement de à près.
Correction
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 4
En déduire le signe de sur l'intervalle .
Correction
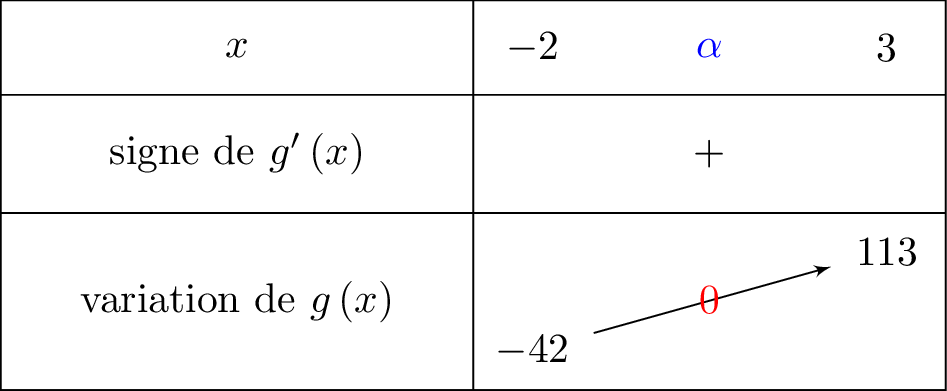
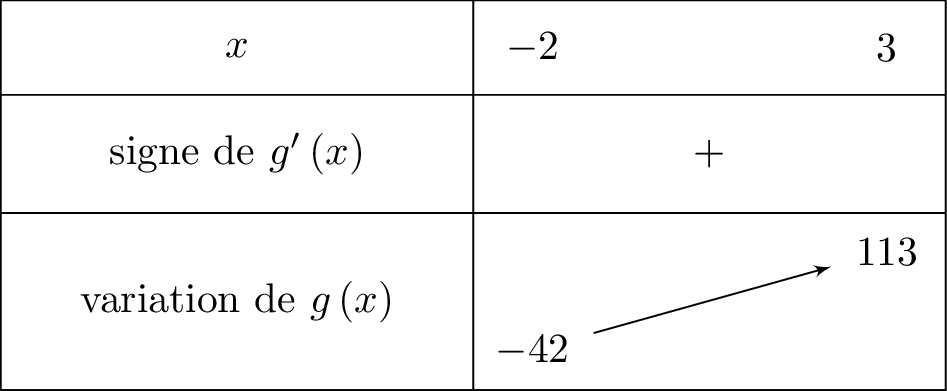
Donc pour tout et pour tout
On résume cela dans un tableau de signe :