Continuité, dérivation, lectures graphiques et convexité

Exercice 1 - Exercice 2

1 min
0
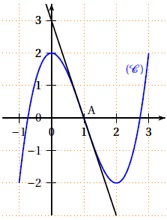
On donne ci-dessous la représentation graphique C\mathscr{C} d'une fonction ff définie et dérivable sur l'intervalle[−1;3]\left[-1;3\right].
On note f′f' la fonction dérivée de ff et FF une primitive de ff .
La tangente à la courbe C\mathscr{C} au point A(1;0)A\left(1;0\right) est tracée, elle passe par le point de coordonnées (0;3)\left(0;3\right).
Question 1

La valeur de f′(1)f'\left(1\right) est :
  • f′(1)=3f'\left(1\right)=3
  • f′(1)=−3f'\left(1\right)=-3
  • f′(1)=−13f'\left(1\right)=-\frac{1}{3}
  • f′(1)=0f'\left(1\right)=0

Correction
La bonne réponse est b.
f′(1)f'\left(1\right) correspond au coefficient directeur de la tangente à la courbe au point d'abscisse 11 donc au point AA.
De plus, le point BB appartient à cette tangente.
A l'aide du point AA et du point BB on va pouvoir donner le coefficient directeur de la tangente .
f′(1)=yB−yAxB−xAf'\left(1\right)=\frac{y_{B} -y_{A} }{x_{B} -x_{A} }
f′(1)=3−00−1=−3f'\left(1\right)=\frac{3-0}{0-1} =-3
Question 2

La fonction ff est :
  • Concave sur [−1;1]\left[-1;1\right]
  • Convexe sur [−1;1]\left[-1;1\right]
  • Concave sur [0;2]\left[0;2\right]
  • Convexe sur [0;2]\left[0;2\right]

Correction
La bonne réponse est a.
  • Lorsque les tangentes sont situées au-dessus de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est concave sur [a,b]\left[a,b\right].
  • Lorsque les tangentes sont situées en dessous de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est convexe sur [a,b]\left[a,b\right].
    On peut également dire que :
  • Lorsque la courbe est située en dessous de ses tangentes sur un intervalle [a,b]\left[a,b\right] alors ff est concave sur [a,b]\left[a,b\right].
  • Lorsque la courbe est située au-dessus de ses tangentes sur un intervalle [a,b]\left[a,b\right] alors ff est convexe sur [a,b]\left[a,b\right].
Sur l'intervalle [−1;1]\left[-1;1\right] la courbe est en-dessous de ses tangentes donc ff est concave sur cet intervalle.
Question 3

On pose I=∫01f(x)dxI=\int _{0}^{1}f\left(x\right)dx .
Un encadrement de II est :
  • 0≤I≤10\le I\le 1
  • 1≤I≤21\le I\le 2
  • 2≤I≤32\le I\le 3
  • 3≤I<43\le I<4

Correction
La bonne réponse est b.
La fonction ff est positive sur [0;1]\left[0;1\right] donc l'intégrale II est positive et est égale à l'aire sous la courbe et l'axe des abscisses et délimité par les droites verticales x=0x=0 et x=1x=1.
Il suffit de compter les nombres de carreaux sous la courbe et l'axe des abscisses et délimité par les droites verticales x=0x=0 et x=1x=1.
Il y a plus d'un carreau mais moins de deux carreaux.
Question 4

Toute primitive FF de la fonction ff est :
  • Croissante sur [0;1]\left[0;1\right]
  • Décroissante sur [0;1]\left[0;1\right]
  • Croissante sur [−1;0]\left[-1;0\right]
  • Croissante sur [−1;1]\left[-1;1\right]

Correction
La bonne réponse est a.
  • Lorsque ff est positive sur [a;b]\left[a;b\right] alors FF est croissante sur [a;b]\left[a;b\right]
  • Lorsque ff est négative sur [a;b]\left[a;b\right] alors FF est décroissante sur [a;b]\left[a;b\right]
Une primitive FF de la fonction ff a pour dérivée cette fonction ff.
Il faut donc étudier le signe ff et on obtiendra les variations de FF.
ff est positive sur [0;1]\left[0;1\right] donc la fonction FF est croissante sur cet intervalle.