Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Reconnaître un schéma de Bernoulli - Exercice 1

5 min
15
Une urne dispose de 77 boules indiscernables au toucher. Il y a deux 22 boules rouges et 55 boules vertes. Le jeu consiste à tirer trois boules successivement avec remise : c'est à dire une première boule est tirée, puis remise dans l'urne avant de tirer une deuxième boule et ainsi de suite. On gagne la partie si l'on ne tire que des rouges lors des 33 tirages.
Question 1

Justifier que le jeu peut être modélisée par un schéma de Bernoulli.

Correction
On considère le tirage d'une boule de l'urne comme une expérience aˋ deux issues :\red{\text{à deux issues :}}
  • RR l’événement : « La boule tirée est rouge »
  • R‾\overline{R} l’événement : « La boule tirée n'est pas rouge , c'est à dire la boule est verte »
    • Cette expérience est donc une eˊpreuve de Bernoulli\red{\text{une épreuve de Bernoulli}} de paramètre p=27p=\frac{2}{7} où pp est la probabilité du succès de l’événement RR.
    On réalise n=3n=3 fois, de manieˋre indeˊpendante\red{\text{de manière indépendante}}, la même épreuve de Bernoulli pour laquelle la probabilité d'un succès p(R)p\left(R\right) est p=27p=\frac{2}{7} .
    Ce jeu correspond bien à un scheˊma de Bernoulli\red{\text{un schéma de Bernoulli}} de paramètres n=3n=3 et p=27p=\frac{2}{7} .
    Question 2

    Représenter ce schéma de Bernoulli par un arbre.

    Correction

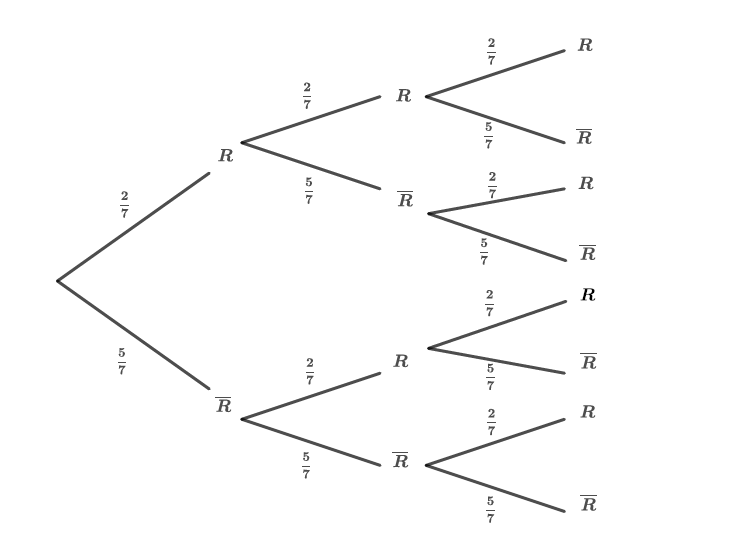
    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.