Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 22ème partie - Exercice 3

25 min
40
Question 1
PARTIE A
L’entreprise produit 4040% de ballons de football de petite taille et 6060% de ballons de taille standard. On admet que 22% des ballons de petite taille et 55% des ballons de taille standard ne sont pas conformes à la réglementation. On choisit un ballon au hasard dans l’entreprise. On considère les évènements :
  • AA : « le ballon de football est de petite taille »,
  • BB : « le ballon de football est de taille standard »,
  • CC : « le ballon de football est conforme à la réglementation» et C‾\overline{C}, l’évènement contraire de CC.

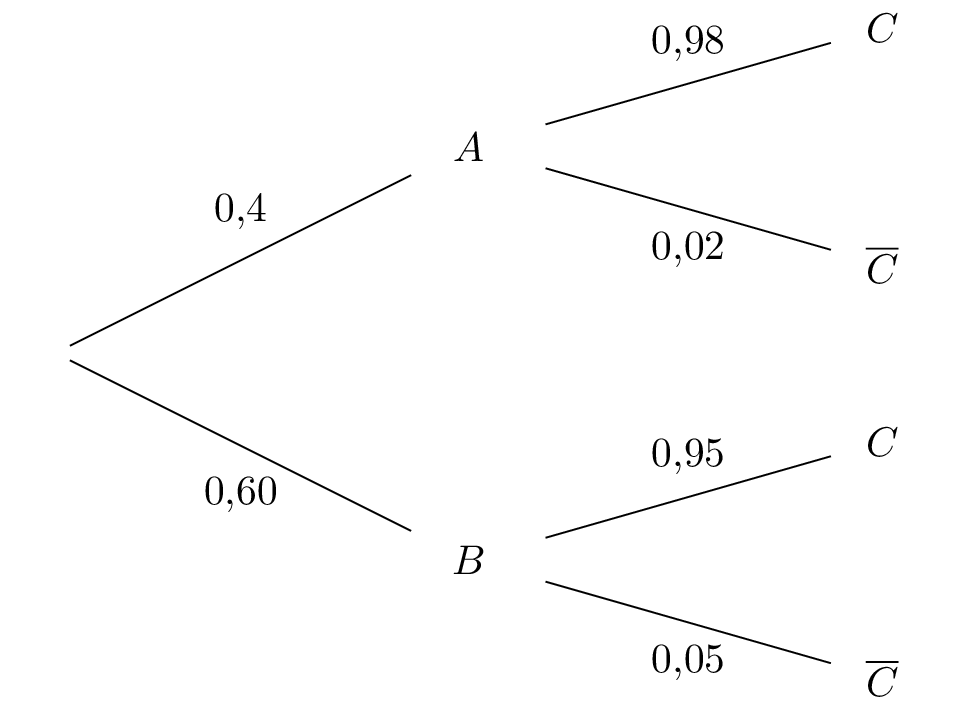
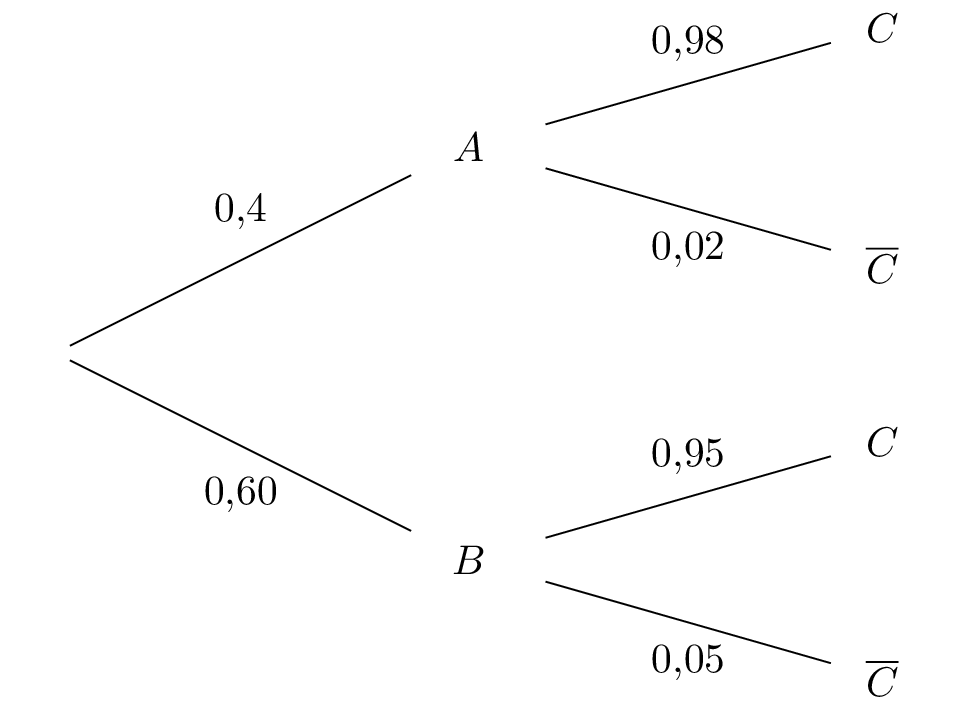
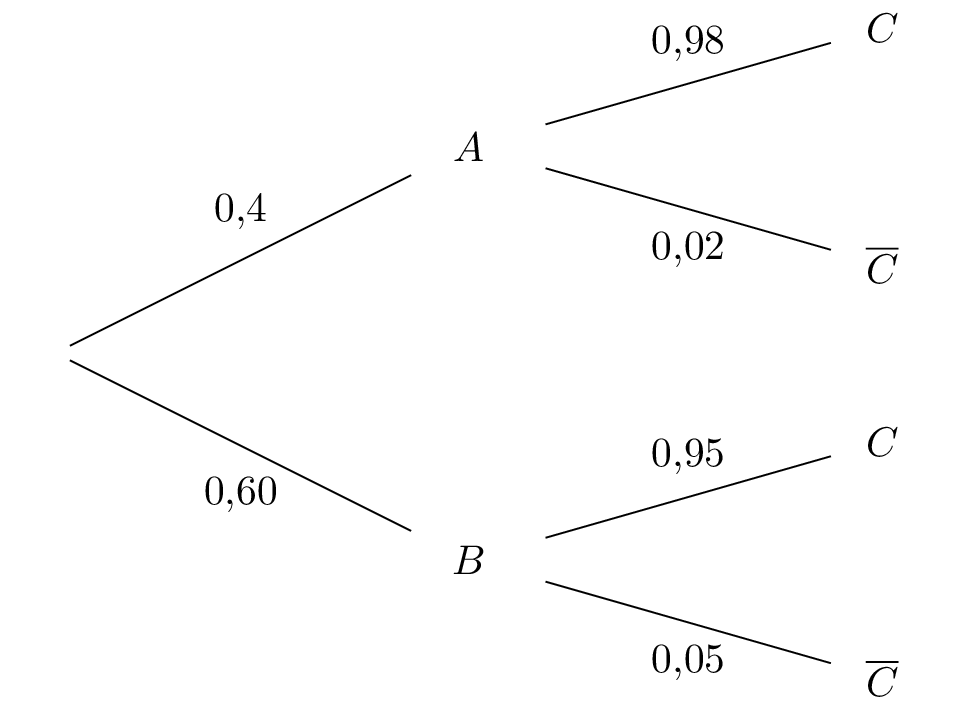
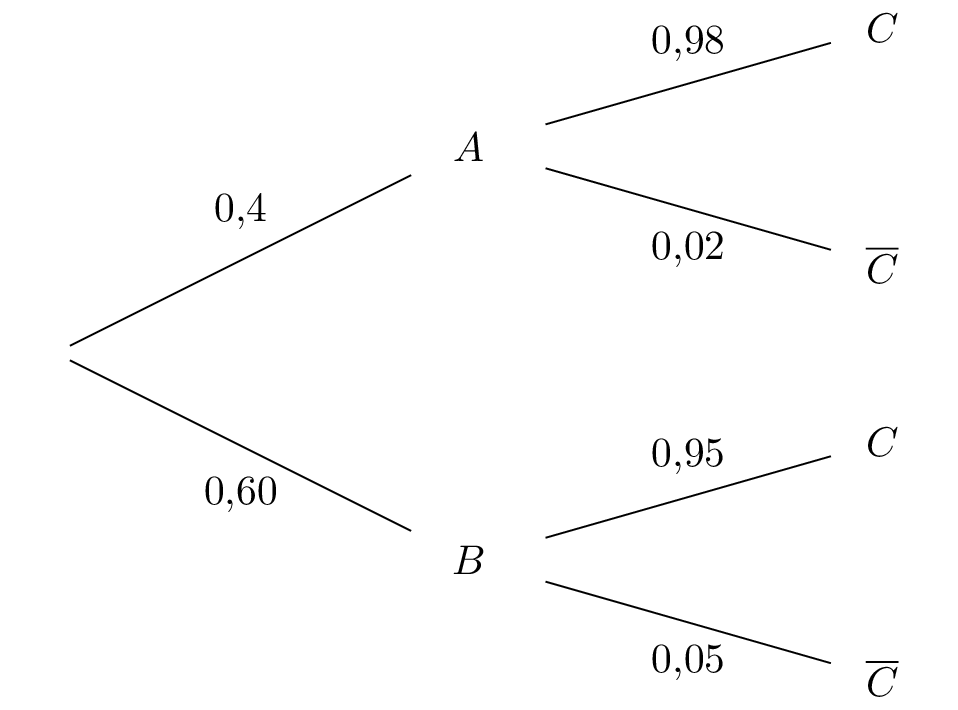
    • Représenter cette expérience aléatoire à l'aide d'un arbre de probabilités.

    Correction
    On représente la situation par un arbre pondéré :
    Question 2

    Calculer la probabilité que le ballon de football soit de petite taille et soit conforme à la réglementation.

    Correction
    « Le ballon de football soit de petite taille et soit conforme à la réglementation » correspond à l’événement A∩CA\cap C.
    Il en résulte que :
    P(A∩C)=P(A)×PA(C)P\left(A\cap C\right)=P\left(A\right)\times P_{A} \left(C\right)
    P(A∩C)=0,4×0,98P\left(A\cap C\right)=0,4\times 0,98
    P(A∩C)=0,392P\left(A\cap C\right)=0,392

    Question 3

    Montrer que la probabilité de l’évènement CC est égale à 0,9620,962.

    Correction
    Les évènements AA et BB forment une partition de l'univers.
    D'après la formule des probabilités totales, on a :
    P(C)=P(A∩C)+P(B∩C)P\left(C\right)=P\left(A \cap C\right)+P\left(B \cap C\right) équivaut successivement à :
    P(C)=P(A)×PA(C)+P(B)×PB(C)P\left(C\right)=P\left(A\right)\times P_{A} \left(C\right)+P\left(B\right)\times P_{B} \left(C\right)
    P(C)=0,392+0,6×0,95P\left(C\right)=0,392 + 0,6\times 0,95
    P(C)=0,962P\left(C\right)=0,962

    Question 4

    Le ballon de football choisi n’est pas conforme à la réglementation. Quelle est la probabilité que ce ballon soit de petite taille? On arrondira le résultat à 10−310^{-3} près.

    Correction
    Il s'agit d'une probabilité conditionnelle PC‾(A)P_{\overline{C}} \left(A\right).
    Ainsi :
    PC‾(A)=P(A∩C‾)P(C‾)P_{\overline{C}} \left(A\right)=\frac{P\left(A\cap \overline{C}\right)}{P\left(\overline{C}\right)}
    PC‾(A)=P(A)×PA(C‾)P(C‾)P_{\overline{C}} \left(A\right)=\frac{P\left(A\right)\times P_{A} \left(\overline{C}\right)}{P\left(\overline{C}\right)}
    PC‾(A)=0,4×0,021−0,962P_{\overline{C}} \left(A\right)=\frac{0,4\times0,02}{1-0,962}
    Ainsi :
    PC‾(A)≈0,211P_{\overline{C}} \left(A\right)\approx0,211

    Question 5
    PARTIE B
    On prélève au hasard un échantillon de 5050 ballons dans la production de cette entreprise. La production est suffisamment importante pour que l'on puisse assimiler ce prélèvement à un tirage avec remise. Soit XX la variable aléatoire qui donne le nombre de ballons conformes de l'échantillon.

    Quelle est la loi de probabilité de la variable aléatoire XX. Préciser ses paramètres.

    Correction
    A chaque tirage la probabilité de tirer un ballon conforme est de 0,9620,962
    On est donc en présence d'un schéma de Bernoulli :
    On appelle succès "tirer un ballon conforme" avec la probabilité p=0,962p=0,962
    On appelle échec "ne pas tirer un ballon conforme" avec la probabilité 1−p=0,0381-p=0,038
    On répète cinquante fois de suite cette expérience de façon indépendante.
    XX est la variable aléatoire qui associe le nombre de ballons conformes dans l'échantillon.
    XX suit la loi binomiale de paramètre n=50n=50 et p=0,962p=0,962
    On note alors X∼B(50;0,962)X \sim B\left(50;0,962 \right)

    Question 6

    Quelle est la probabilité que l'échantillon prélevé comporte exactement 4949 ballons conformes? On arrondira le résultat à 10−310^{-3} près.

    Correction
    Pour le calcul de P(X=49)P\left(X=49\right),
  • Avec une Texas :\red{\text{Avec une Texas :}} pour P(X=49)P\left(X=49\right) on tape : (cf. fiche Utiliser la loi binomiale avec une Texas)
    2nd - DISTR -- puis choisir
    • BinomFdp(valeur de nn, valeur de pp, valeur de kk) c'est-à-dire ici : BinomFdp(5050; 0,9620,962 ; 4949) puis taper sur enter et on obtient :
    P(X=49)≈0,285P\left(X=49\right)\approx 0,285
    arrondi à 10−310^{-3} près.
    Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.
  • Avec une calculatrice Casio Graph 35+ ou modeˋle supeˊrieur :\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}} (cf. fiche Utiliser la loi binomiale avec une Casio)
    • Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
    On remplit le tableau de la manière qui suit :
    D.P. Binomiale
    Data Variable
    xx : 4949 Valeur de kk
    Numtrial : 5050 Valeur de nn
    pp : 0,9620,962 Valeur de pp

    Puis taper sur EXE et on obtient :
    P(X=49)≈0,285P\left(X=49\right)\approx 0,285
    arrondi à 10−310^{-3} près.
    Question 7

    Quelle est la probabilité que l'échantillon prélevé comporte au moins 4848 ballons conformes? On arrondira le résultat à 10−310^{-3} près.

    Correction
    Il nous faut calculer ici la probabilité P(X≥48)P\left(X\ge48\right).
    Or P(X≥48)=P(X=48)+P(X=49)+P(X=50)P\left(X\ge48\right)=P\left(X=48\right)+P\left(X=49\right)+P\left(X=50\right)
    On appliquer la même méthode que dans la question 66 pour calculer P(X=48)P\left(X=48\right) ; P(X=49)P\left(X=49\right) et P(X=50)P\left(X=50\right).
    Il en résulte que :
    P(X≥48)≈0,704P\left(X\ge48\right)\approx0,704
    arrondi à 10−310^{-3} près.

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.