Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 22ème partie - Exercice 2

25 min
40
Une enquête a été réalisée auprès des élèves d’un lycée afin de connaître leur sensibilité au développement durable et leur pratique du tri sélectif. L’enquête révèle que 7070% des élèves sont sensibles au développement durable, et, parmi ceux qui sont sensibles au développement durable, 8080% pratiquent le tri sélectif. Parmi ceux qui ne sont pas sensibles au développement durable, on en trouve 1010% qui pratiquent le tri sélectif.
On interroge un élève au hasard dans le lycée. On considère les évènements suivants :
  • SS : L’élève interrogé est sensible au développement durable.
  • TT : L’élève interrogé pratique le tri sélectif.
    • Les résultats seront arrondis à 10−210^{-2}
    Question 1

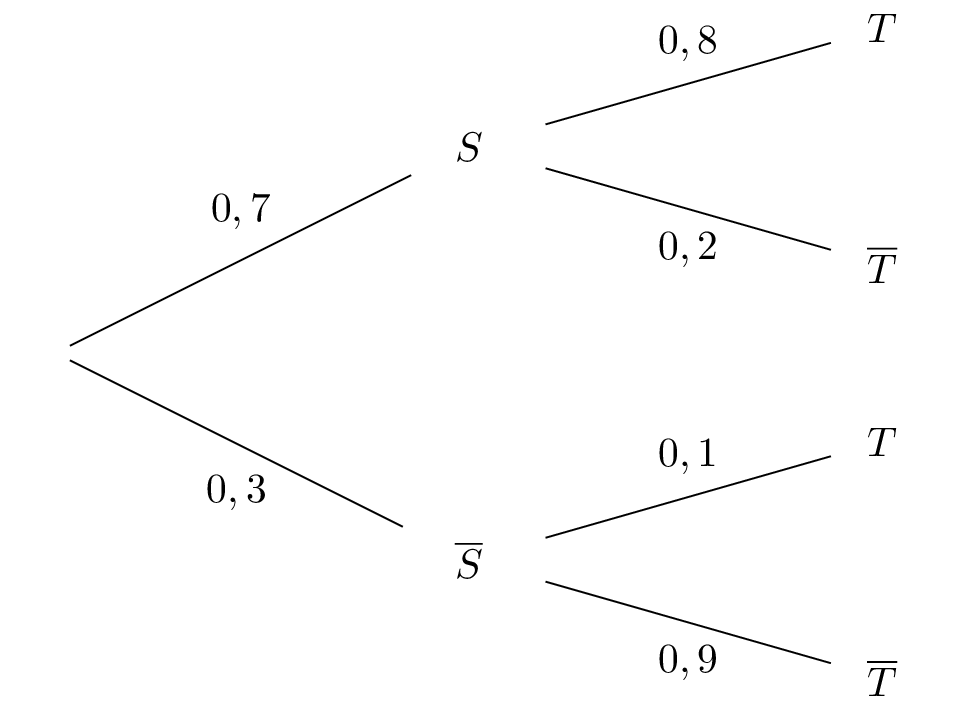
    Construire un arbre pondéré décrivant la situation.

    Correction
    D'après l'énoncé on obtient l'arbre suivant :
    Question 2

    Calculer la probabilité que l’élève interrogé soit sensible au développement durable et pratique le tri sélectif.

    Correction
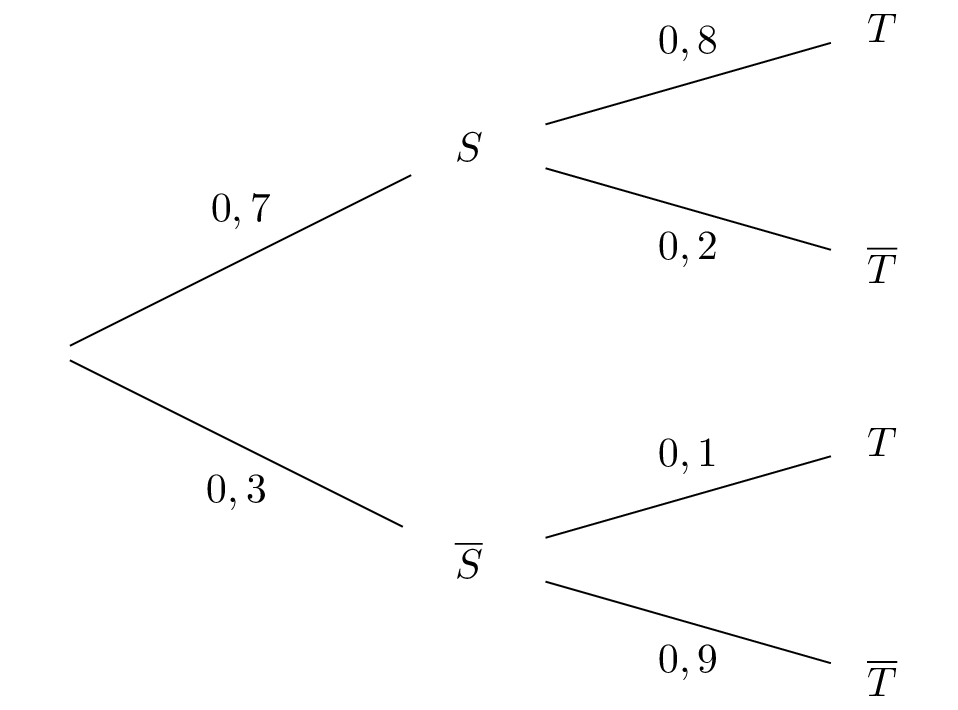
    L’évènement «l’élève interrogé est sensible au développement durable et pratique le tri sélectif» se traduit par : S∩TS\cap T.
    Il en résulte que :
    P(S∩T)=P(A)×PS(T)P\left(S\cap T\right)=P\left(A\right)\times P_{S} \left(T\right)
    P(S∩T)=0,7×0,8P\left(S\cap T\right)=0,7\times 0,8
    P(S∩T)=0,56P\left(S\cap T\right)=0,56

    Question 3

    Montrer que la probabilité P(T)P\left(T\right) de l’évènement TT est 0,590,59.

    Correction
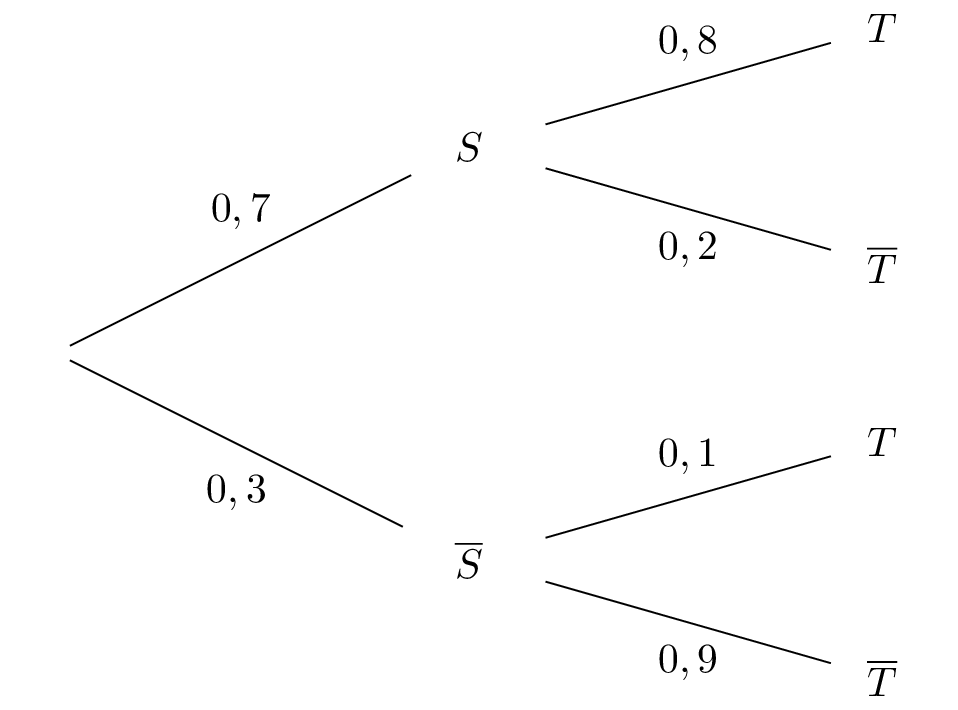
    Les évènements SS et S‾\overline{S} forment une partition de l'univers.
    D'après la formule des probabilités totales, on a :
    P(T)=P(S∩T)+P(S‾∩T)P\left(T\right)=P\left(S \cap T\right)+P\left(\overline{S} \cap T\right) équivaut successivement à :
    P(T)=P(S)×PS(T)+P(S‾)×PS‾(T)P\left(T\right)=P\left(S\right)\times P_{S} \left(T\right)+P\left(\overline{S}\right)\times P_{\overline{S}} \left(T\right)
    P(T)=0,7×0,8+0,3×0,1P\left(T\right)=0,7\times 0,8 + 0,3\times 0,1
    P(T)=0,59P\left(T\right)=0,59

    Question 4

    On interroge un élève qui ne pratique pas le tri sélectif. Peut-on affirmer que les chances qu’il se dise sensible au développement durable sont inférieures à 1010%?

    Correction
    Il s'agit ici de déterminer une probabilité conditionnelle. Il nous faut donc calculer PT‾(S)P_{\overline{T}} \left(S\right).
    PT‾(S)=P(S∩T‾)P(T‾)P_{\overline{T}} \left(S\right)=\frac{P\left(S\cap \overline{T}\right)}{P\left(\overline{T}\right)}
    PT‾(S)=P(S∩T‾)1−P(T)P_{\overline{T}} \left(S\right)=\frac{P\left(S\cap \overline{T}\right)}{1-P\left(T\right)}
    PT‾(S)=0,7×0,21−0,59P_{\overline{T}} \left(S\right)=\frac{0,7\times 0,2}{1-0,59}
    PT‾(S)≈0,34P_{\overline{T}} \left(S\right)\approx0,34

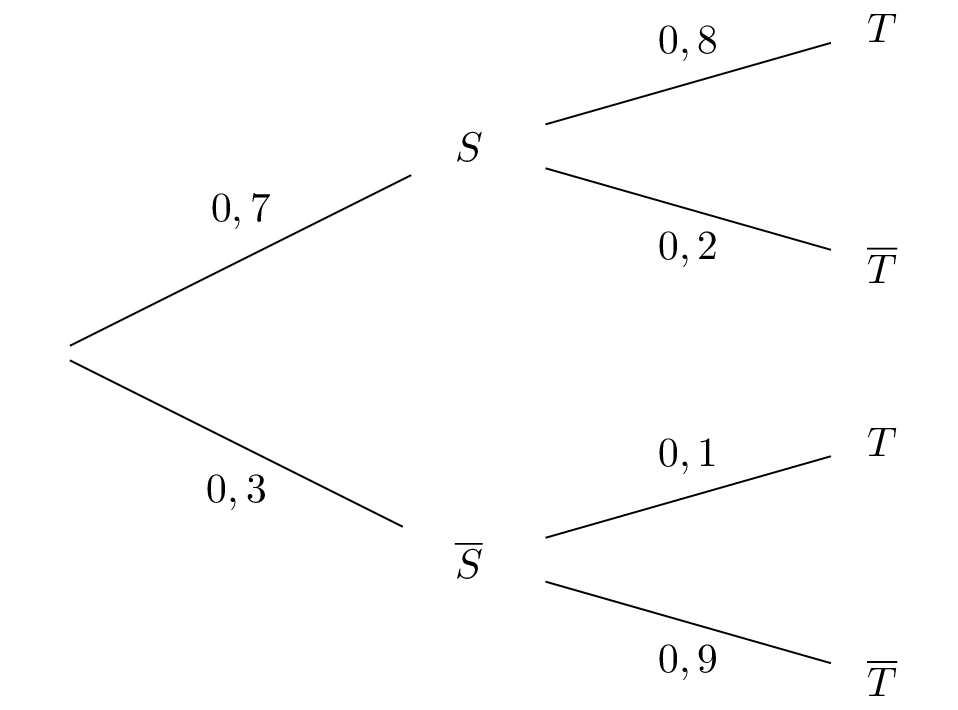
    Les chances qu’il se dise sensible au développement durable sont de 3434% donc on en pas affirmation est fausse.
    Question 5
    On interroge successivement et de façon indépendante quatre élèves pris au hasard parmi les élèves de l’établissement. Soit XX la variable aléatoire qui donne le nombre d’élèves pratiquant le tri sélectif parmi les 44 élèves interrogés.

    Définir la loi XX et indiquer ses paramètres.

    Correction
    A chaque tirage la probabilité d'interroger un élève pratiquant le tri sélectif est 0,590,59.
    On est donc en présence d'un schéma de Bernoulli :
    On appelle succès « interroger un élève pratiquant le tri sélectif » avec la probabilité p=0,59p=0,59
    On appelle échec « ne pas interroger un élève pratiquant le tri sélectif » avec la probabilité 1−p=0,411-p=0,41
    On répète quatre fois de suite cette expérience de façon indépendante.
    XX est la variable aléatoire qui associe le nombre d’élèves pratiquant le tri sélectif dans l'échantillon .
    XX suit la loi binomiale de paramètre n=4n=4 et p=0,59p=0,59 .
    On note alors XX∼\simB(4;0,59)B\left(4;0,59\right)

    Question 6

    Calculer la probabilité qu’aucun des quatre élèves interrogés ne pratique le tri sélectif.

    Correction
    La probabilité qu’aucun des quatre élèves ne pratique le tri sélectif est : P(X=0)P\left(X=0\right)
    Avec une Texas :\red{\text{Avec une Texas :}} pour P(X=0)P\left(X=0\right) on tape :
    2nd - DISTR -- puis choisir
    BinomFdp(valeur de nn, valeur de pp, valeur de kk) c'est-à-dire ici BinomFdp(44, 0.590.59 , 00) puis on tape sur enter et on obtient :
    P(X=0)≈0,03P\left(X=0\right)\approx 0,03
    arrondi à 10−310^{-3} près.
    Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.

    Avec une calculatrice Casio Graph 35+ ou modeˋle supeˊrieur :\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}} pour P(X=0)P\left(X=0\right) on tape :
    Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
    On remplit le tableau de la manière qui suit :
    D.P. Binomiale
    Data Variable
    xx : 00 Valeur de kk
    Numtrial : 44 Valeur de nn
    pp : 0,590,59 Valeur de pp

    puis on tape sur EXE et on obtient :
    P(X=0)≈0,03P\left(X=0\right)\approx 0,03
    arrondi à 10−210^{-2} près.
    Question 7

    Calculer la probabilité qu’au moins deux des quatre élèves interrogés pratiquent le tri sélectif.

    Correction
    La probabilité qu’au moins deux des quatre élèves pratiquent le tri sélectif est : P(X≥2)P\left(X\ge2\right)
    Or : P(X≥2)=P(X=2)+P(X=3)+P(X=4)P\left(X\ge2\right)=P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)
    Ainsi :
    P(X≥2)≈0,3511+0,3368+0,1212≈0,81P\left(X\ge2\right)\approx0,3511+0,3368+0,1212\approx0,81

    Deuxième méthode : Nous aurions pu prendre l'évènement contraire : P(X≥2)P\left(X\ge2\right)
    P(X≥2)=1−P(X≤1)P\left(X\ge2\right)=1-P\left(X\le1\right)
    P(X≥2)=1−(P(X=0)+P(X=1))P\left(X\ge2\right)=1-\left(P\left(X=0\right)+P\left(X=1\right)\right)
    P(X≥2)≈1−(0,0283+0,1627)≈0,81P\left(X\ge2\right)\approx1-\left(0,0283+0,1627\right)\approx0,81