Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 22ème partie - Exercice 1

30 min
45
Une usine fabrique des étuis en cuir pour téléphone mobile. Chaque étui produit est soumis à deux contrôles :
  • Un contrôle de qualité de finition : l’étui ne doit pas présenter de défaut définition
  • Un contrôle de solidité : l'étui est exclu de la vente s'il n'est pas solide.
    • Il s'avère, à la suite d'un grand nombre de vérifications, que :
  • 9494% des étuis sont sans défaut de finition; parmi les étuis qui sont dans défaut de finition, 9696% réussissent le test de solidité.
  • 22% des étuis ne satisfont à aucun des deux contrôles.
    • Question 1
    On prend au hasard un étui parmi les étuis produits. On note :
  • FF l'évènement : " l'étui est sans défaut de finition "
  • SS l'évènement : " l'étui réussit le rest de solidité "

    • En utilisant l'énoncé, préciser : P(F)P\left(F\right) ; PF(S)P_{F} \left(S\right) et P(F‾∩S‾)P\left(\overline{F}\cap \overline{S}\right)

    Correction
    D'après l'énoncé, on a :
  • P(F)=0,94P\left(F\right)=0,94
  • PF(S)=0,96P_{F} \left(S\right)=0,96
  • P(F‾∩S‾)=0,02P\left(\overline{F}\cap \overline{S}\right)=0,02
    • Question 2

    Démontrer que : PF‾(S‾)=13P_{\overline{F}} \left(\overline{S}\right)=\frac{1}{3}

    Correction
    Il s'agit d'une probabilité conditionnelle. Il vient alors :
    PF‾(S‾)=P(F‾∩S‾)P(F‾)P_{\overline{F}} \left(\overline{S}\right)=\frac{P\left(\overline{F}\cap \overline{S}\right)}{P\left(\overline{F}\right)}
    PF‾(S‾)=0,020,06P_{\overline{F}} \left(\overline{S}\right)=\frac{0,02}{0,06}
    Ainsi :
    PF‾(S‾)=13P_{\overline{F}} \left(\overline{S}\right)=\frac{1}{3}
    Question 3

    Donner au complet l'arbre pondéré correspondant à cette situation.

    Correction
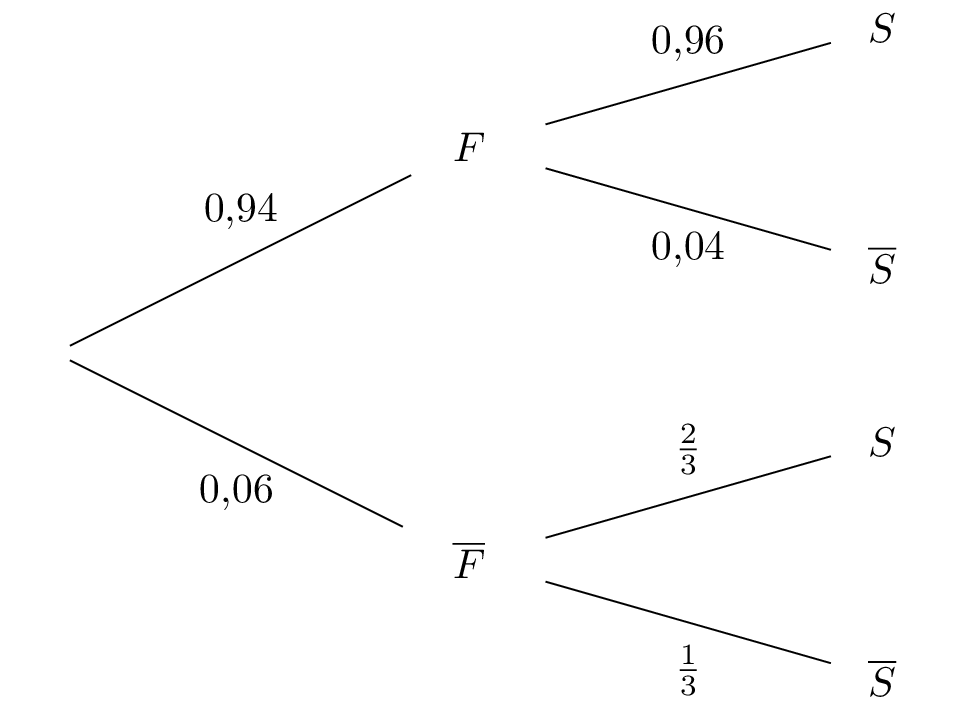
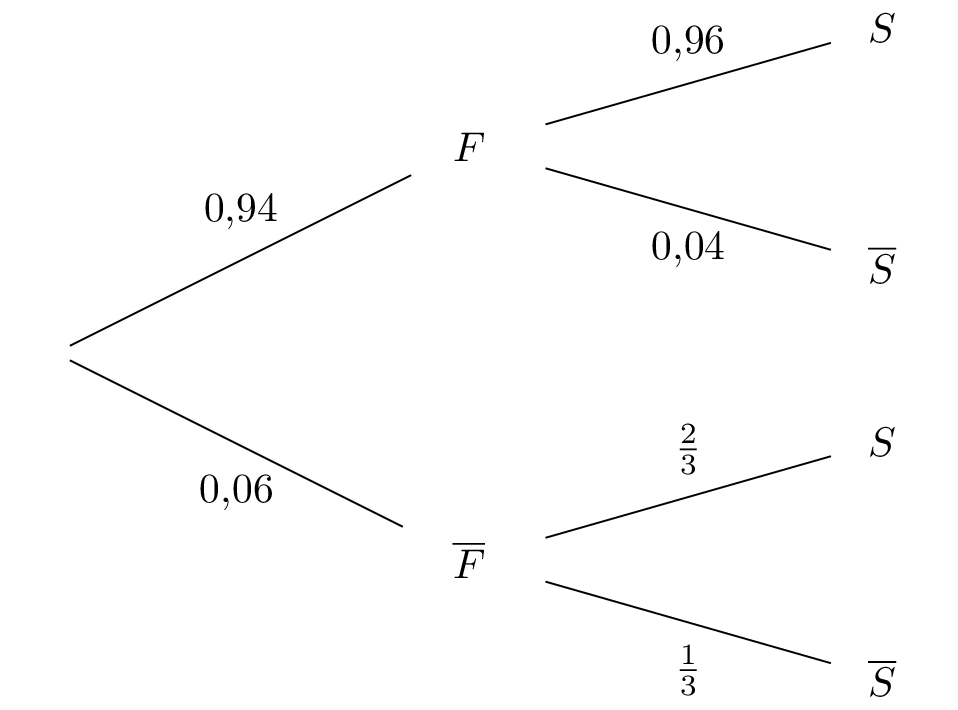
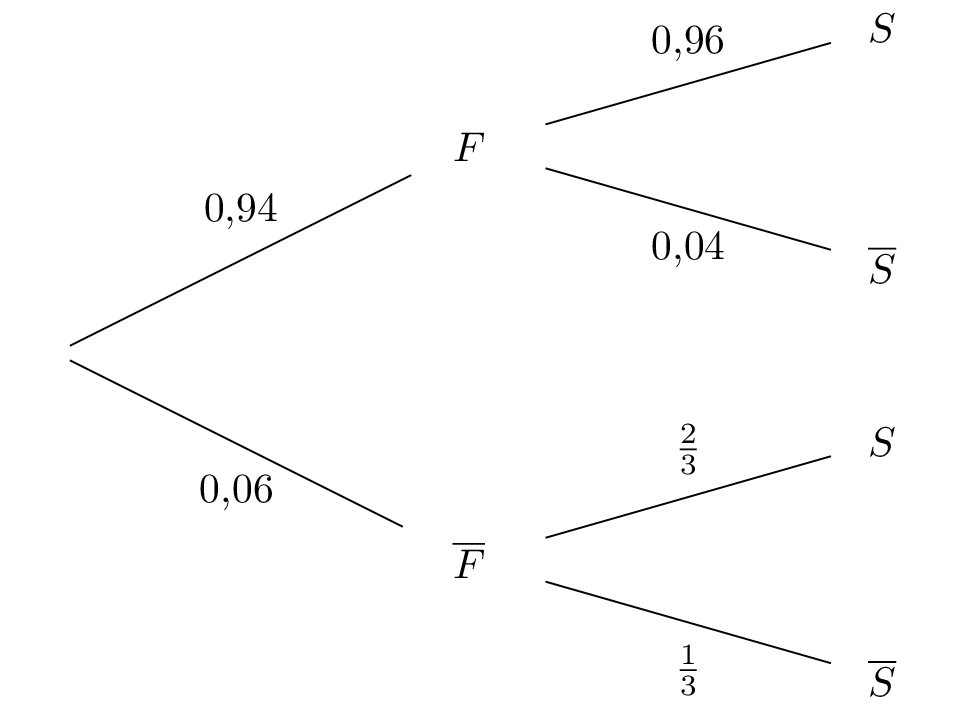
    On représente la situation par un arbre pondéré :
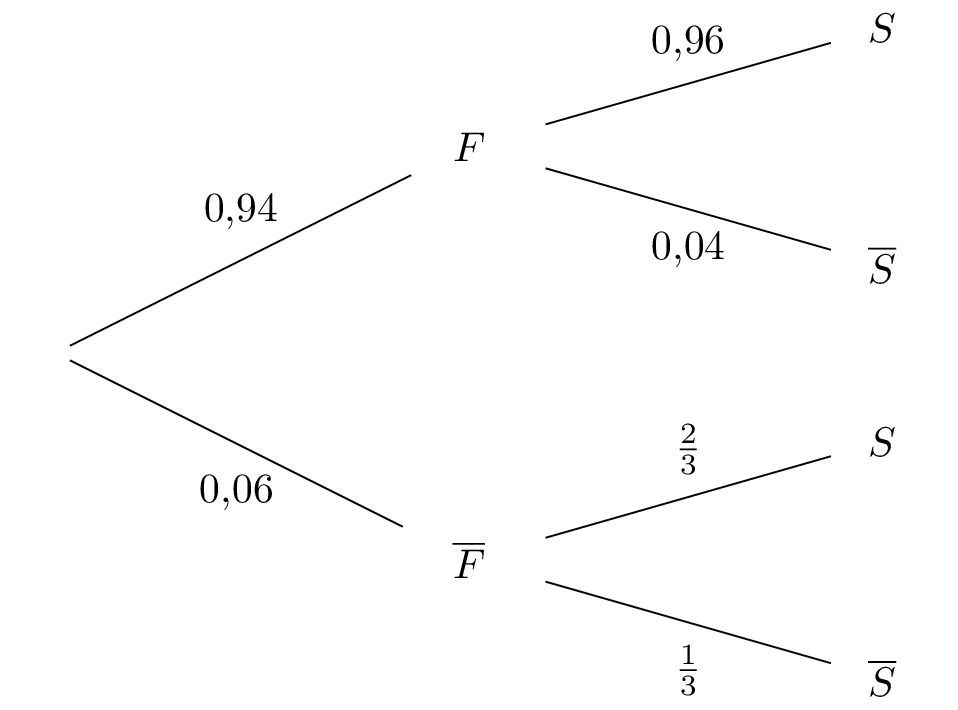
    Question 4

    Démontrer que P(S)=0,9424P\left(S\right)=0,9424

    Correction
    Les évènements FF et F‾\overline{F} forment une partition de l'univers.
    D'après la formule des probabilités totales, on a :
    P(S)=P(F∩S)+P(F‾∩S)P\left(S\right)=P\left(F \cap S\right)+P\left(\overline{F} \cap S\right) équivaut successivement à :
    P(S)=P(F)×PF(S)+P(F‾)×PF‾(S)P\left(S\right)=P\left(F\right)\times P_{F} \left(S\right)+P\left(\overline{F}\right)\times P_{\overline{F}} \left(S\right)
    P(S)=0,94×0,96+0,06×23P\left(S\right)=0,94\times0,96 + 0,06\times \frac{2}{3}
    P(S)=0,9424P\left(S\right)=0,9424
    Question 5

    Un étui a réussi le test de solidité. Calculer la probabilité qu'il soit sans défaut de finition. On donnera le résultat arrondi au dix-millième.

    Correction
    Il s'agit à nouveau d'une probabilité conditionnelle :
    PS(F)=P(F∩S)P(S)P_{S} \left(F\right)=\frac{P\left(F\cap S\right)}{P\left(S\right)}
    PS(F)=0,94×0,960,9424P_{S} \left(F\right)=\frac{0,94\times0,96}{0,9424}
    Ainsi :
    PS(F)≈0,9576P_{S} \left(F\right)\approx0,9576

    Question 6
    Les étuis ayant satisfait les deux contrôles rapportent un bénéfice de 55 euros, ceux qui n'ont pas satisfait au test de solidité ne rapportent rien. Les autres étuis rapportent un bénéfice de 33 euros.
    On désigne par YY la variable aléatoire qui associe à chaque étui le bénéfice rapporté.

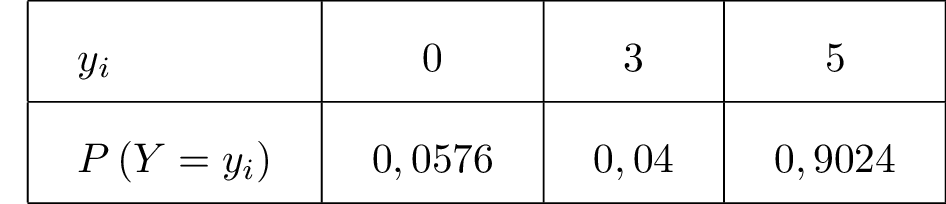
    Déterminer la loi de probabilité de la variable YY.

    Correction
    Dans cette question les valeurs prises par YY sont : Y={0;3;5}Y=\left\{0;3;5\right\}
  • P(F∩S)=0,94×0,96=0,9024P\left(F \cap S\right)=0,94\times0,96=0,9024. Donc P(Y=5)=0,9024P\left(Y=5\right)=0,9024
  • P(S‾)=1−P(S)=1−0,9424=0,0576P\left(\overline{S}\right)=1-P\left(S\right)=1-0,9424=0,0576. Donc P(Y=0)=0,0576P\left(Y=0\right)=0,0576
  • P(F‾∩S)=0,06×23=0,04P\left(\overline{F} \cap S\right)=0,06\times\frac{2}{3}=0,04. Donc P(Y=3)=0,04P\left(Y=3\right)=0,04
    • La loi de probabilité de la variable YY est donnée ci-dessous :
    Question 7

    Calculer l'espérance mathématique de la variable aléatoire YY et interpréter le résultat.

    Correction
      On appelle l’espérance mathématique de la variable XX, la quantité notée E(X)E\left(X\right) définie par :
    • E(X)=∑xi×pi=x1×p1+x2×p2+…+xn×pnE\left(X\right)=\sum x_{i} \times p_{i} =x_{1} \times p_{1}+x_{2} \times p_{2}+\ldots+ x_{n} \times p_{n}
     Calcul de l’espeˊrance.\red{\text{ Calcul de l'espérance.}}
    E(Y)=0×0,0576+3×0,04+5×0,9024E\left(Y\right)=0\times 0,0576 +3\times 0,04 +5\times 0,9024
    Soit
    E(Y)=4,632E\left(Y\right)=4,632

    En moyenne, un étui rapporte 4,6324,632 euros à l'entreprise.
    Question 8
    On prélève au hasard dans la production de l'entreprise un lot de 2020 étuis. On désigne par XX la variable aléatoire égale au nombre d'étuis de ce lot ne réussissant pas le test de solidité.
    On suppose que la quantité fabriquée est suffisamment importante pour que la constitution de ce lot puisse être assimilée à un tirage avec remise.

    Déterminer la loi de probabilité de la variable aléatoire XX et préciser ses paramètres.

    Correction
    A chaque tirage la probabilité que l'étui ne réussisse pas le test de solidité est de 0,05760,0576
    On est donc en présence d'un schéma de Bernoulli :
    On appelle succès "l'étui ne réussit pas le test de solidité" avec la probabilité p=0,0576p=0,0576
    On appelle échec "l'étui réussit le test de solidité" avec la probabilité 1−p=0,94241-p=0,9424
    On répète vingt fois de suite cette expérience de façon indépendante.
    XX est la variable aléatoire qui associe le nombre de ballons conformes dans l'échantillon.
    XX suit la loi binomiale de paramètre n=20n=20 et p=0,0576p=0,0576
    On note alors X∼B(20;0,0576)X \sim B\left(20;0,0576 \right)
    Question 9

    Calculer au millième près, la probabilité qu'au moins 22 étuis du lot ne passent pas le test de solidité.

    Correction
    Il nous faut calculer ici la probabilité P(X≥2)P\left(X\ge2\right).
    Or P(X≥2)=1−P(X≤1)P\left(X\ge2\right)=1-P\left(X\le1\right)
    P(X≥2)=1−(P(X=0)+P(X=1))P\left(X\ge2\right)=1-\left(P\left(X=0\right)+P\left(X=1\right)\right)
    P(X≥2)=1−P(X=0)−P(X=1)P\left(X\ge2\right)=1-P\left(X=0\right)-P\left(X=1\right)
    Avec la calculatrice, on obtient :
    P(X≥2)≈0,322P\left(X\ge2\right)\approx0,322
    .

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.