Exercices types : $$1$$^ère partie - Exercice 3

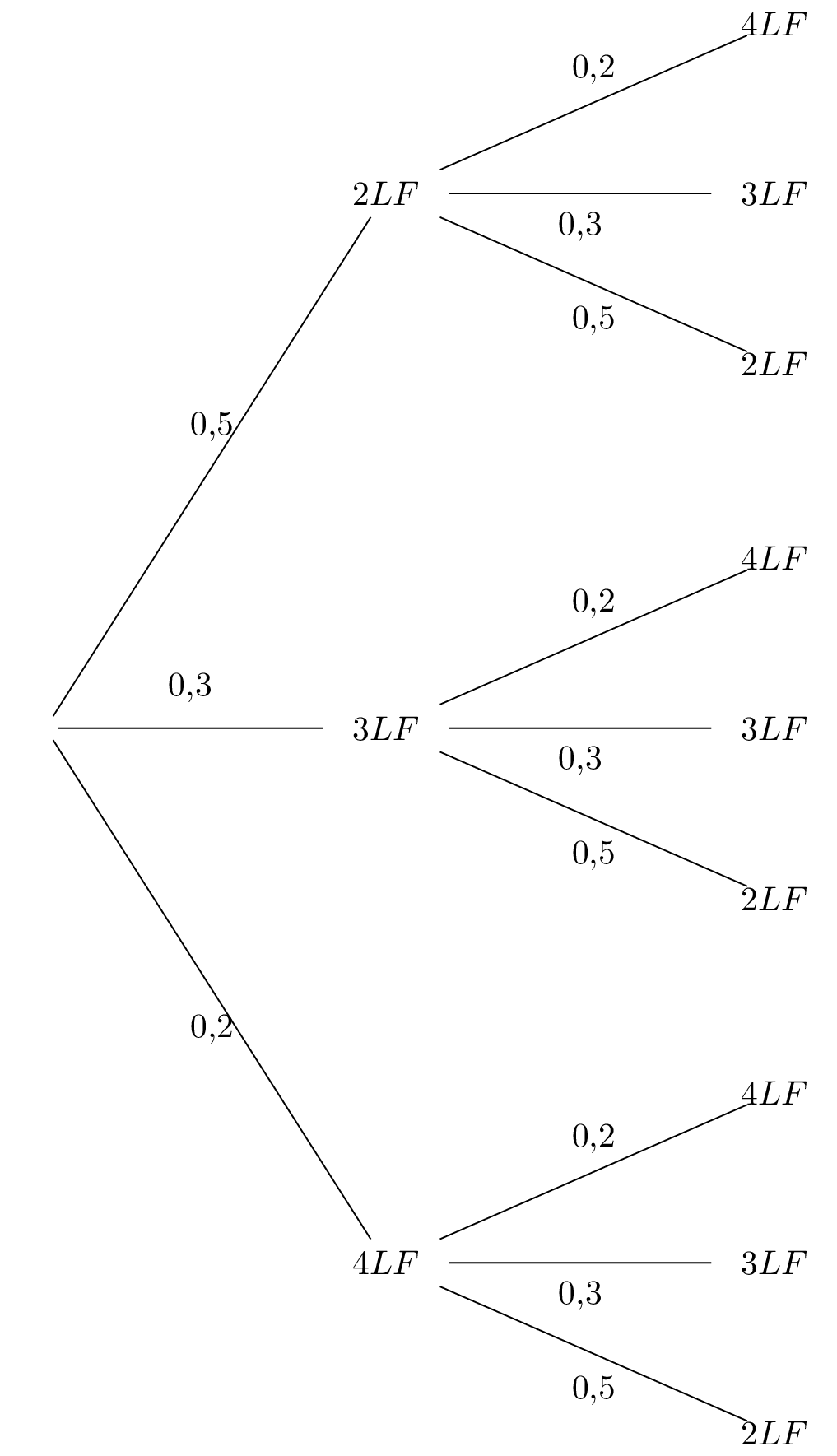
D'après l'énoncé, on en déduit l'arbre pondéré suivant :
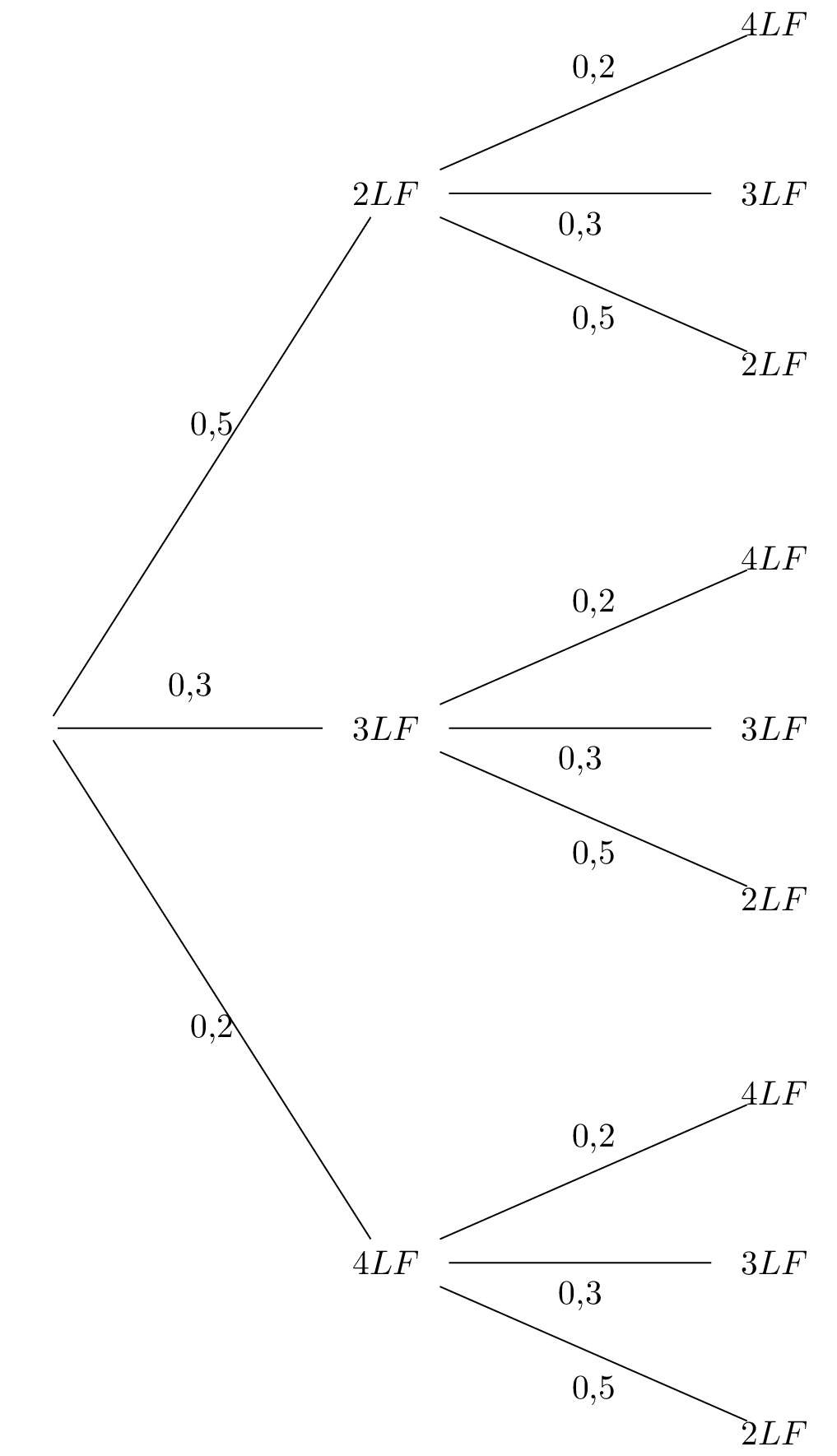Il faut calculer la valeur de $$P\left(X=8\right)$$ car le joueur doit marquer $$4$$ lancers francs lors de la première série et la même chose lors de la deuxième série.
Il vient alors que :
$$P\left(X=8\right)=0,2\times 0,2$$
$$P\left(X=8\right)=\frac{1}{25}$$

$$X$$ prend les valeurs suivantes $$8$$, $$7$$, $$6$$, $$5$$ et $$4$$ donc $$X\in \left\{8;7;6;5;4\right\}$$

• $$P\left(X=8\right)=\frac{1}{25}$$
  (vu à la question précédente)
• $$P\left(X=7\right)=0,2\times 0,3+0,3\times 0,2$$ , donc :
  $$P\left(X=7\right)=\frac{3}{25}$$
• $$P\left(X=6\right)=0,2\times 0,5+0,3\times 0,3+0,5\times 0,2$$, donc :
  $$P\left(X=6\right)=\frac{29}{100}$$
• $$P\left(X=5\right)=0,3\times 0,5+0,5\times 0,3$$ , donc :
  $$P\left(X=5\right)=\frac{3}{10}$$
• $$P\left(X=4\right)=0,5\times 0,5$$ , donc :
  $$P\left(X=4\right)=\frac{1}{4}$$

On peut donc dresser la loi de probabilité de $$X$$ :

$$E\left(X\right)=4\times \frac{1}{4} +5\times \frac{3}{10} +6\times \frac{29}{100} +7\times \frac{3}{25} +8\times \frac{1}{25}$$

En moyenne, un joueur marquera $$5,4$$ lancers francs par séance d'entrainements.

$$P\left(X\ge 6\right)=P\left(X=6\right)+P\left(X=7\right)+P\left(X=8\right)$$.
On a vu à la question 2, les valeurs des probabilités.
Ainsi :
$$P\left(X\ge 6\right)=\frac{29}{100} +\frac{3}{25} +\frac{1}{25}$$
$$P\left(X\ge 6\right)=\frac{9}{20}$$
Donc la probabilité pour qu'un joueur réussisse son entrainement est égale à $$\frac{9}{20}$$

On doit calculer $$P\left(Y=9\right)$$
$$\red{\text{Avec une Texas :}}$$ on tape pour $$P\left(Y=9\right)$$
2^nd - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k ) c'est-à-dire ici BinomFdp(9, $$\frac{9}{20}$$ , 9) puis taper sur enter et on obtient $$P\left(Y=9\right)\approx 7,567\times 10^{-4}$$ arrondi à $$10^{-3}$$ près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.

$$\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}}$$ on tape pour $$P\left(Y=9\right)$$
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :

puis on tape sur EXE et on obtient $$P\left(Y=9\right)\approx 7,567\times 10^{-4}$$ arrondi à $$10^{-3}$$ près.

On doit calculer $$P\left(Y=6\right)$$
$$\red{\text{Avec une Texas :}}$$ on tape pour $$P\left(Y=6\right)$$
2^nd - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k ) c'est-à-dire ici BinomFdp(9, $$\frac{9}{20}$$ , 6) puis on tape sur enter et on obtient $$P\left(Y=6\right)\approx 0,117$$ arrondi à $$10^{-3}$$ près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.
$$\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}}$$ on tape pour $$P\left(Y=6\right)$$
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit

puis on tape sur EXE et on obtient : $$P\left(Y=6\right)\approx 0,117$$ arrondi à $$10^{-3}$$ près.

On doit calculer $$P\left(Y\ge 1\right)$$.
Or : $$P\left(Y\ge 1\right)=1-P\left(Y=0\right)$$
Pour le calcul de $$P\left(Y=0\right)$$

Avec une calculatrice Texas, on tape pour $$P\left(Y=0\right)$$
2^nd - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k ) c'est-à-dire ici BinomFdp($$9$$, $$\frac{9}{20}$$ , $$0$$) puis on tape sur enter et on obtient : $$P\left(Y=0\right)\approx 0,0046$$ arrondi à $$10^{-4}$$ près.
$$\red{\text{Avec une Texas :}}$$ on aura BinomPdf au lieu de BinomFdp.
Enfin : $$P\left(Y\ge 1\right)=1-P\left(Y=0\right)$$
D'où :
$$\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}}$$ on tape pour $$P\left(Y=0\right)$$
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :

puis on tape sur EXE et on obtient : $$P\left(Y=0\right)\approx 0,0046$$ arrondi à $$10^{-4}$$ près.
Enfin : $$P\left(Y\ge 1\right)=1-P\left(Y=0\right)$$
D'où :

Soit $$n$$ le nombre d'entrainements auxquels doit participer un joueur pour que la probabilité d'avoir au moins un succès soit supérieure à $$0,99$$.
On a :
$$P\left(Y\ge 1\right)\ge 0,99$$ équivaut successivement à
$$1-P\left(Y=0\right)\ge 0,99$$ . On rappelle que : $$P\left(Y=0\right)=\left(\begin{array}{c} {n} \\ {0} \end{array}\right)\times \left(\frac{9}{20} \right)^{0} \times \left(1-\frac{9}{20} \right)^{n}$$
$$1-\left(\begin{array}{c} {n} \\ {0} \end{array}\right)\times \left(\frac{9}{20} \right)^{0} \times \left(1-\frac{9}{20} \right)^{n} \ge 0,99$$
$$1-\left(\frac{11}{20} \right)^{n} \ge 0,99$$
$$\left(\frac{11}{20} \right)^{n} \le 0,01$$
$$\ln \left(\frac{11}{20} \right)^{n} \le \ln \left(0,01\right)$$
$$n\times \ln \left(\frac{11}{20} \right)\le \ln \left(0,01\right)$$ , or $$\ln \left(\frac{11}{20} \right)\le 0$$
$$n\ge \frac{\ln \left(0,01\right)}{\ln \left(\frac{11}{20} \right)}$$
$$n\ge 7,70$$ donc $$n\ge 8$$
Il faut donc au moins $$8$$ entrainements pour que la probabilité d'avoir au moins un succès soit supérieure à $$0,99$$.