Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Exercices types : 11ère partie - Exercice 2

25 min
40
Dans une classe de terminale S section Européenne les étudiants doivent passer le TOEIC.
  • 75%75\% ont réussi le test.
  • Parmi ceux qui ont réussi, 80%80\% le passaient pour la première fois.
  • Parmi ceux qui ont échoué au test, 5%5\% le passaient pour la première fois.
On considère les évènements TT : « l'élève a réussi le TOEIC », et AA : « l'élève a passé le test plusieurs fois ».
Question 1

Dresser un arbre pondéré décrivant la situation.

Correction
On dresse l'arbre pondéré grâce aux informations données par l'énoncé.
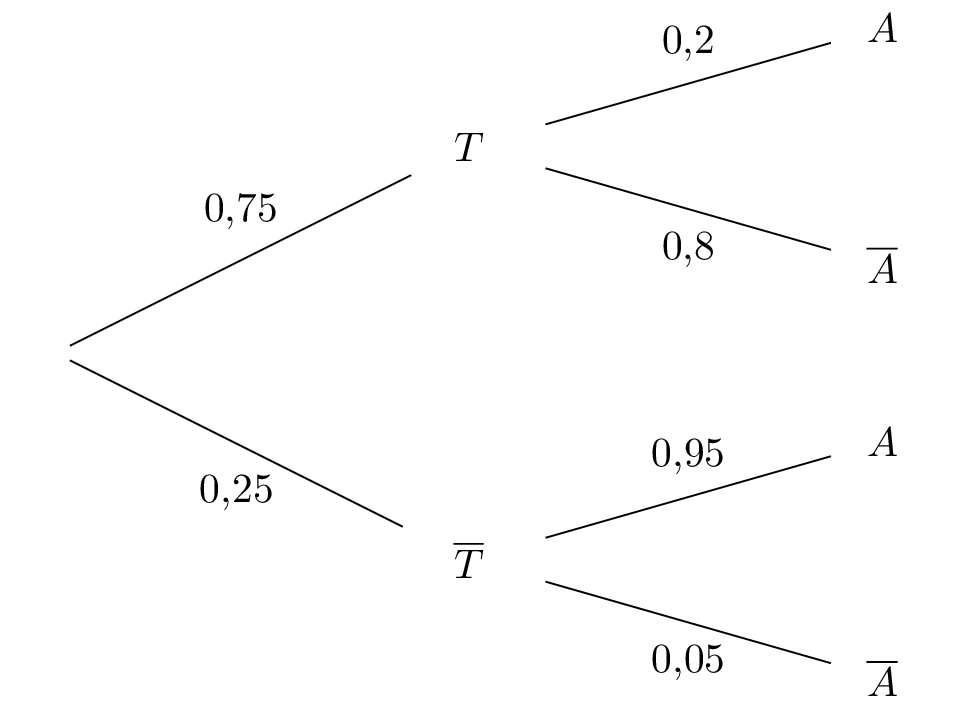
Ainsi :
Question 2

Calculer la probabilité qu'un élève choisi au hasard ait passé le test pour la première fois et l'ait réussi.

Correction
On calcule alors :
P(T∩A‾)=P(T)×PT(A‾)P\left(T\cap \overline{A}\right)=P\left(T\right)\times P_{T} \left(\overline{A}\right)
P(T∩A‾)=0,75×0,8P\left(T\cap \overline{A}\right)=0,75\times 0,8
P(T∩A‾)=0,6P\left(T\cap \overline{A}\right)=0,6
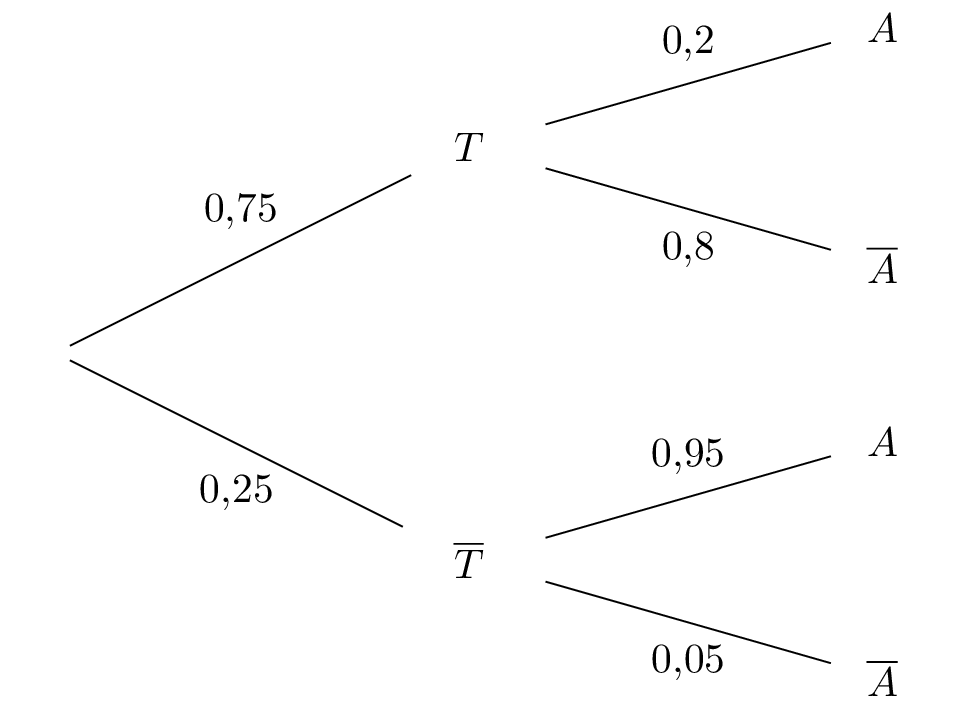
La probabilité qu'un élève choisi au hasard ait passé le test pour la première fois et l'ait réussi est de 0,60,6.
Question 3

Déterminer la probabilité qu'un élève choisi au hasard ait passé plusieurs fois le test.

Correction
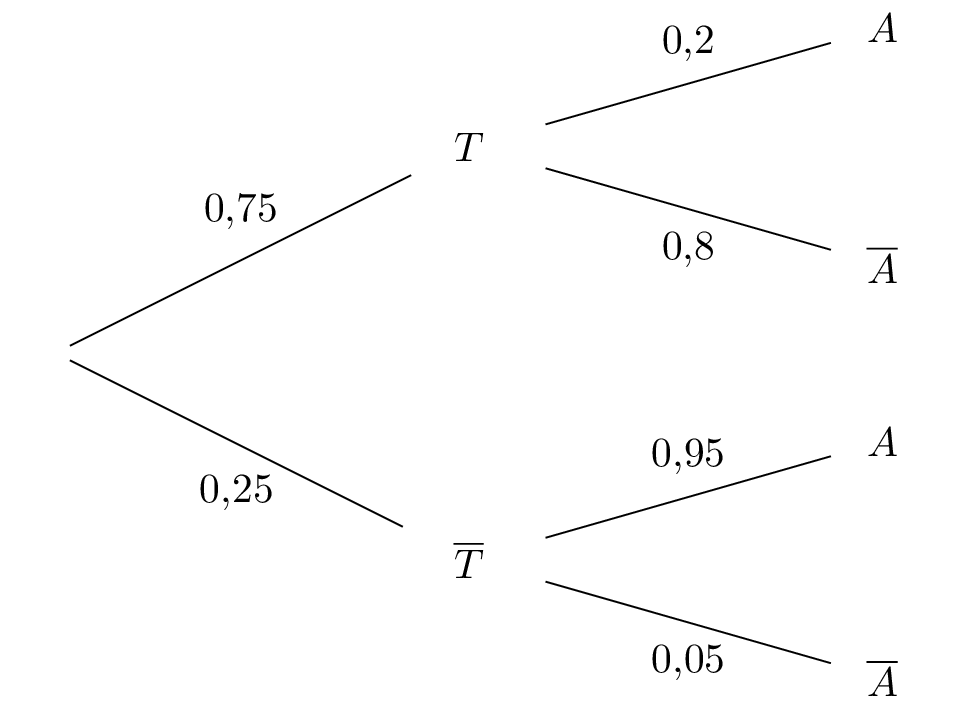
Les évènements TT et T‾\overline{T} forment une partition de l'univers.
D'après la formule des probabilités totales, on a :
p(A)=P(T∩A)+P(T‾∩A)p\left(A\right)=P\left(T\cap A\right)+P\left(\overline{T}\cap A\right) équivaut successivement à
p(A)=P(T)×pT(A)+P(T‾)×pT‾(A)p\left(A\right)=P\left(T\right)\times p_{T} \left(A\right)+P\left(\overline{T}\right)\times p_{\overline{T}} \left(A\right)
p(A)=0,75×0,2+0,25×0,95p\left(A\right)=0,75\times 0,2+0,25\times 0,95
p(A)=0,15+0,2375p\left(A\right)=0,15+0,2375
p(A)=0,3875p\left(A\right)=0,3875
La probabilité qu'un élève choisi au hasard ait passé plusieurs fois le test est de 0,38750,3875.
Question 4

On choisit au hasard un élève ayant passé plusieurs fois le test.
Quelle est la probabilité qu'il ait réussie ?

Correction
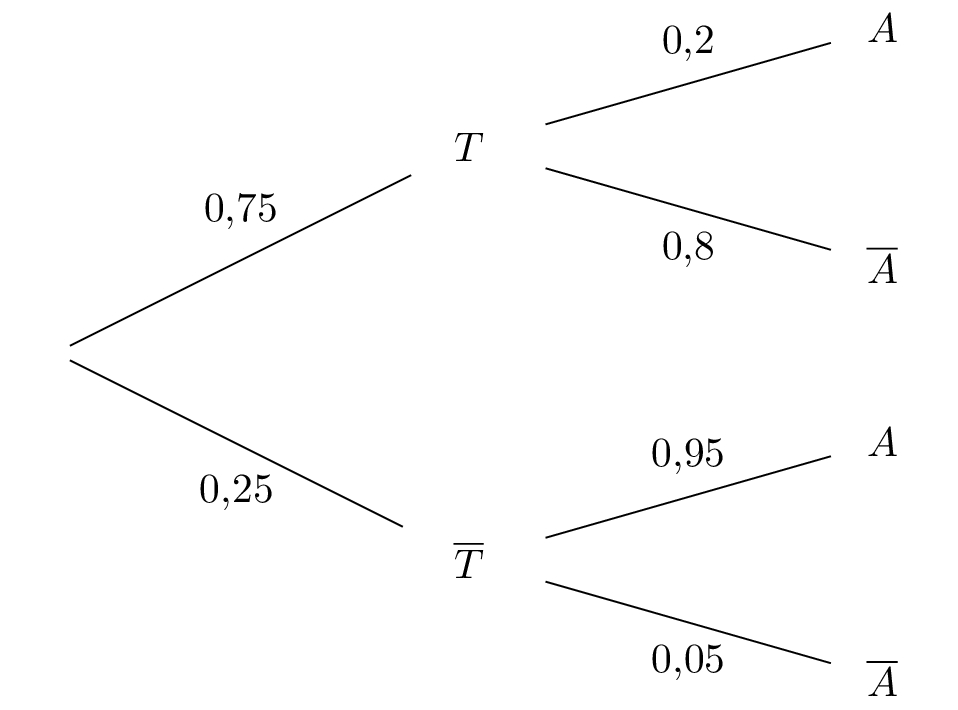
L'énoncé de la question nous indique qu'il faut calculer pA(T)p_{A} \left(T\right).
D'après les formules du cours on sait que : pA(T)=P(T∩A)P(A)p_{A} \left(T\right)=\frac{P\left(T\cap A\right)}{P\left(A\right)} .
Il vient alors que : pA(T)=0,75×0,20,3875p_{A} \left(T\right)=\frac{0,75\times 0,2}{0,3875} d'où pA(T)=1231p_{A} \left(T\right)=\frac{12}{31}
Question 5
Après l'épreuve, 10 amis se retrouvent entre eux pour fêter la fin des examens.
On note XX la variable aléatoire qui associe le nombre d'étudiants à réussir le TOEIC.

Définir la loi XX et indiquer ses paramètres.

Correction
A chaque tirage la probabilité de tirer un ami ayant réussi le TOEIC est 34\frac{3}{4} .
On est donc en présence d'un schéma de Bernoulli :
On appelle succès « tirer un ami ayant réussi le TOEIC » avec la probabilité p=34p=\frac{3}{4}
On appelle échec « tirer un ami n'ayant pas réussi le TOEIC » avec la probabilité 1−p=141-p=\frac{1}{4}
On répète dix fois de suite cette expérience de façon indépendante.
XX est la variable aléatoire qui associe le nombre d'étudiants à réussir le TOEIC.
XX suit la loi binomiale de paramètre n=10n=10 et p=34p=\frac{3}{4} .
On note alors XX∼\simB(10;34)B\left(10;\frac{3}{4} \right)

Question 6

Quelle est la probabilité qu'il y ait au moins un élève ayant réussi l'épreuve du TOEIC ?

Correction
On doit calculer : P(X≥1)P\left(X\ge 1\right).
Or P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
Pour le calcul de P(X=0)P\left(X=0\right) :
Avec une Texas :\red{\text{Avec une Texas :}} pour P(X=0)P\left(X=0\right) on tape :
(tu peux regarder la fiche "Utiliser la loi binomiale avec une Texas" pour plus de détails)
2nd - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(10, 34\frac{3}{4} , 0) puis on tape sur enter et on obtient :
P(X=0)≈9,53×10−7P\left(X=0\right)\approx 9,53\times 10^{-7}
arrondi à 10−310^{-3} près.
Pour certaines versions de Texas, on aura BinomPdf au lieu de BinomFdp.
Enfin : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
D'où :
P(X≥1)≈1−9,53×10−7≈0,999999P\left(X\ge 1\right)\approx 1-9,53\times 10^{-7} \approx 0,999999

Avec une calculatrice Casio Graph 35+ ou modeˋle supeˊrieur :\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}} pour P(X=0)P\left(X=0\right) :
(tu peux regarder la fiche "Utiliser la loi binomiale avec une Casio" pour plus de détails)
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
D.P. Binomiale
Data Variable
xx : 00 Valeur de kk
Numtrial : 1010 Valeur de nn
pp : 34\frac{3}{4} Valeur de pp

puis on tape sur EXE et on obtient :
P(X=0)≈9,53×10−7P\left(X=0\right)\approx 9,53\times 10^{-7}
arrondi à 10−310^{-3} près.
Enfin : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
D'où :
P(X≥1)≈1−9,53×10−7≈0,999999P\left(X\ge 1\right)\approx 1-9,53\times 10^{-7} \approx 0,999999

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.