Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Epreuve d'enseignement de spécialité Session Métropole 11 septembre 2023 sujet 1 Exercice 3 : Probabilités conditionnelles et loi binomiale - Exercice 1

25 min
45
Les parties A et B sont indépendantes.
Les probabilités demandées seront données à 10−310^{-3} près.
Pour aider à la détection de certaines allergies, on peut procéder à un test sanguin dont le résultat est soit positif, soit négatif.
Dans une population, ce test donne les résultats suivants :
  • Si un individu est allergique, le test est positif dans 97%97\% des cas;
  • Si un individu n’est pas allergique, le test est négatif dans 95,7%95,7\% des cas.
    • Par ailleurs, 20%20\% des individus de la population concernée présentent un test positif.
    On choisit au hasard un individu dans la population, et on note :
  • AA l’évènement « l’individu est allergique »;
  • TT l’évènement « l’individu présente un test positif ».
    • On notera A‾\overline{A} et T‾\overline{T} les évènements contraires de AA et TT . On appelle par ailleurs xx la probabilité de l’évènement AA : x=p(A)x = p\left(A\right).
    Partie A.
    Question 1

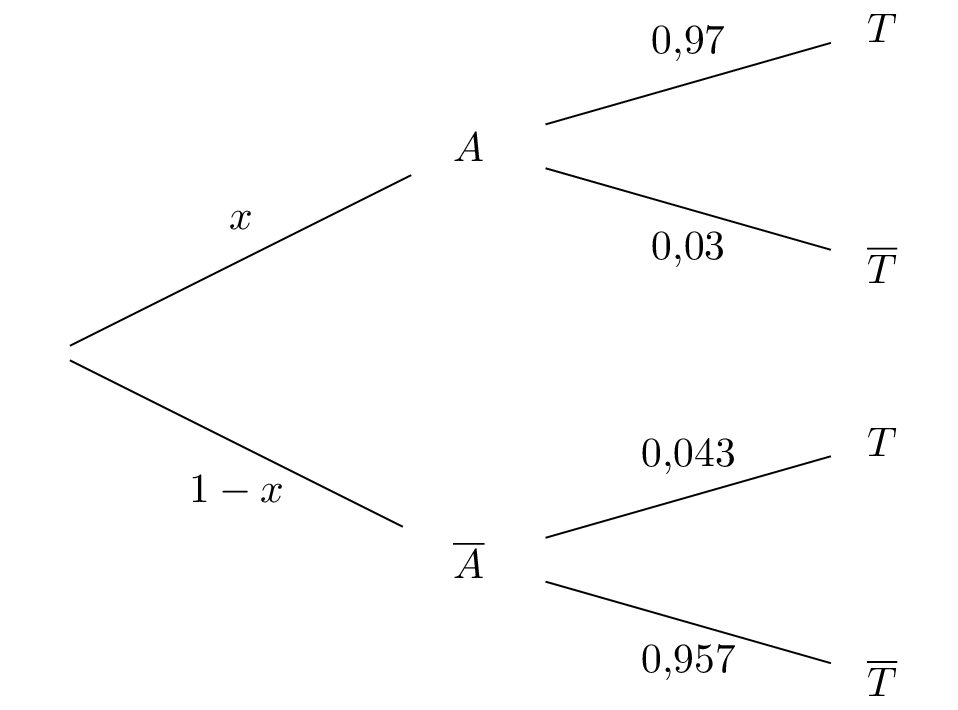
    Reproduire et compléter l’arbre ci-dessous décrivant la situation, en indiquant sur chaque branche la probabilité correspondante.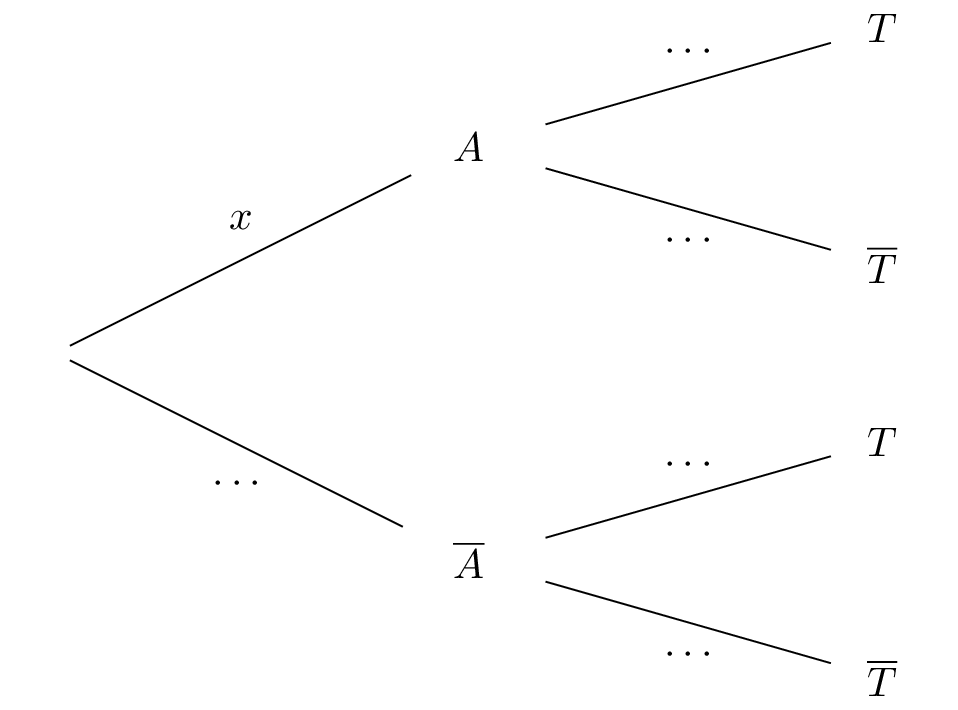

    Correction
    Question 2

    Démontrer l’égalité : p(T)=0,927x+0,043p\left(T\right) = 0,927x +0,043.

    Correction
    Les évènements AA et A‾\overline{A} forment une partition de l'univers.
    D'après la formule des probabilités totales, on a :
    p(T)=p(A∩T)+p(A‾∩T)p\left(T\right)=p\left(A\cap T\right)+p\left(\overline{A}\cap T\right)
    p(T)=p(A)×pA(T)+p(A‾)×pA‾(T)p\left(T\right)=p\left(A\right)\times p_A\left(T\right)+p(\overline{A})\times p_{\overline{A}}\left(T\right)
    p(T)=x×0,97+(1−x)×0,043p\left(T\right)=x\times 0,97+\left(1-x\right)\times 0,043
    p(T)=0,97x+0,043−0,043xp\left(T\right)=0,97x+0,043-0,043x
    Ainsi :
    p(T)=0,927x+0,043p\left(T\right)=0,927x+0,043

    Question 3

    En déduire la probabilité que l’individu choisi soit allergique.

    Correction
    Nous souhaitons calculer la valeur de x=p(A)x = p\left(A\right).
    D'après les hypothèses, 20%20\% des individus de la population concernée présentent un test positif.
    Il en résulte donc que p(T)=0,2 p\left(T\right)=0,2.
    D'après la question précédente, on a sait que : p(T)=0,927x+0,043p\left(T\right)=0,927x+0,043
    il en résulte donc que :
    0,2=0,927x+0,0430,2=0,927x+0,043
    0,927x+0,043=0,20,927x+0,043=0,2
    0,927x=0,2−0,0430,927x=0,2-0,043
    0,927x=0,1570,927x=0,157
    x=0,1570,927x=\frac{0,157}{0,927}
    D'après les hypothèses, les probabilités demandées seront données à 10−310^{-3} près.
    Ainsi :
    p(A)=x≈0,169p\left(A\right)=x\approx 0,169

    La probabilité que l’individu choisi soit allergique est alors d'environ 0,1690,169 .
    Question 4

    Justifier par un calcul l’affirmation suivante :
    « Si le test d’un individu choisi au hasard est positif, il y a plus de 80%80\% de chances que cet individu soit allergique ».

    Correction
    On souhaite déterminer la probabilité pT(A)p_T\left(A\right) et vérifier ensuite que pT(A)>0,8p_T\left(A\right)>0,8
      On note PB(A)P_{B} \left(A\right) la probabilité d’avoir l’événement AA sachant que l’événement BB est réalisé. On a alors la relation suivante :
    • PB(A)=P(A∩B)P(B)P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}
    pT(A)=p(A∩T)p(T)p_{T} \left(A\right)=\frac{p\left(A\cap T\right)}{p\left(T\right)}
    pT(A)=p(A)×pA(T)p(T)p_{T} \left(A\right)=\frac{p\left(A\right)\times p_{A} \left(T\right)}{p\left(T\right)}
    pT(A)=p(A)×pA(T)p(T)p_{T} \left(A\right)=\frac{p\left(A\right)\times p_{A} \left(T\right)}{p\left(T\right)} . D'après la question 33, on a : p(A)=x≈0,169p\left(A\right)=x\approx 0,169
    pT(A)≈0,169×0,970,2p_{T} \left(A\right)\approx\frac{0,169\times 0,97}{0,2}
    pT(A)≈0,82p_{T} \left(A\right)\approx 0,82

    L’affirmation est vraie.
    Question 5

    Partie B.
    On réalise une enquête sur les allergies dans une ville en interrogeant 150150 habitants choisis au hasard, et on admet que ce choix se ramène à des tirages successifs indépendants avec remise.
    On sait que la probabilité qu’un habitant choisi au hasard dans cette ville soit allergique est égale à 0,080,08.
    On note XX la variable aléatoire qui à un échantillon de 150150 habitants choisis au hasard associe le nombre de personnes allergiques dans cet échantillon.
    Quelle est la loi de probabilité suivie par la variable aléatoire XX ? Préciser ses paramètres.

    Correction
    Reˊdaction type pour la loi binomiale :\purple{\text{Rédaction type pour la loi binomiale :}}
    On considère l'expérience ci-dessous aˋ deux issues :\red{\text{à deux issues :}}
  • On appelle succeˋs\red{\text{succès}} « la personne est allergique » avec la probabilité p=0,08p=0,08
  • On appelle eˊchec\red{\text{échec}} « la personne n'est pas allergique » avec la probabilité 1−p=0,921-p=0,92
    • On répète 150150 fois de suite cette expérience de Bernoulli de façon indeˊpendante\red{\text{façon indépendante}}.
    On est donc en présence d’un scheˊma de Bernoulli.\red{\text{d'un schéma de Bernoulli.}}
    XX est la variable aléatoire qui associe le nombre de personnes allergiques parmi les 150150 habitants.
    XX suit la loi binomiale de paramètre n=150n=150 et p=0,08p=0,08
    On note alors XX suit la loi binomiale B(150;0,08)\mathscr{B}\left(150;0,08\right)

    Question 6

    Déterminer la probabilité que 2020 personnes exactement parmi les 150150 interrogées soient allergiques.

    Correction
    Il nous faut calculer P(X=20)P\left(X=20\right)
    Avec la formule du cours :\blue{\text{Avec la formule du cours :}}
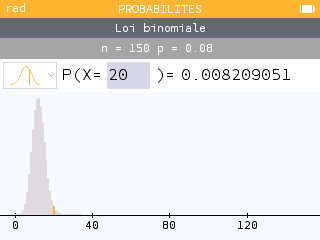
    Soit XX une variable aléatoire suivant la loi binomiale B(n;p)\mathscr{B}\left(n;p\right) alors, pour tout entier kk compris entre 00 et nn, on a :
  • P(X=k)=(nk)pk(1−p)n−kP\left(X=k\right)=\left(\begin{array}{c} {n} \\ {k} \end{array}\right)p^{k} \left(1-p\right)^{n-k}
    • Ainsi :
    P(X=20)=(15020)×(0,08)20×(0,92)130≈0,00082P\left(X=20\right)=\left(\begin{array}{c} {150} \\ {20} \end{array}\right)\times \left(0,08\right)^{20} \times \left(0,92\right)^{130} \approx 0,00082
    Question 7

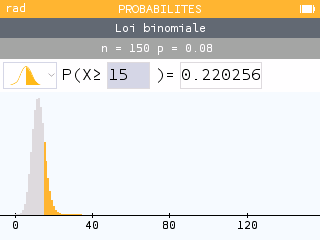
    Déterminer la probabilité qu’au moins 10%10\% des personnes parmi les 150150 interrogées soient allergiques.

    Correction
    10%10\% des personnes parmi les 150150 interrogées correspond à 1515 personnes.
    Il faut donc calculer P(X≥15)P\left(X\ge15\right).
    D'après la calculatrice, on a :