Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

Epreuve d'enseignement de spécialité Session 19 Mai 2022 sujet 2 Exercice 1 : Probabilités conditionnelles et des SUITES - Exercice 1

25 min

Dans une région touristique, une société propose un service de location de vélos pour la journée.La société dispose de deux points de location distinctes, le point

A

et le point

B

.
Les vélos peuvent être empruntés et restitués indifféremment dans l’un où l’autre des deux points de location.
On admettra que le nombre total de vélos est constant et que tous les matins, à l’ouverture du service, chaque vélo se trouve au point

A

ou au point

B

.
D’après une étude statistique :
• Si un vélo se trouve au point

A

un matin, la probabilité qu’il se trouve au point

A

le matin suivant est égale à

0,84

;
• Si un vélo se trouve au point

B

un matin la probabilité qu’il se trouve au point

B

le matin suivant est égale à

0,76

.
À l’ouverture du service le premier matin, la société a disposé la moitié de ses vélos au point

A

, l’autre moitié au point

B

.
On considère un vélo de la société pris au hasard.
Pour tout entier naturel non nul n, on définit les évènements suivants :
•

A_n

: « le vélo se trouve au point

A

n

^ièmematin »
•

B_n

: « le vélo se trouve au point

B

n

^ièmematin ».
Pour tout entier naturel non nul

n

, on note

a_n

la probabilité de l’évènement

A_n

b_n

la probabilité de l’évènement

B_n

. Ainsi

a_1 = 0,5

b_1 = 0,5

Question 1

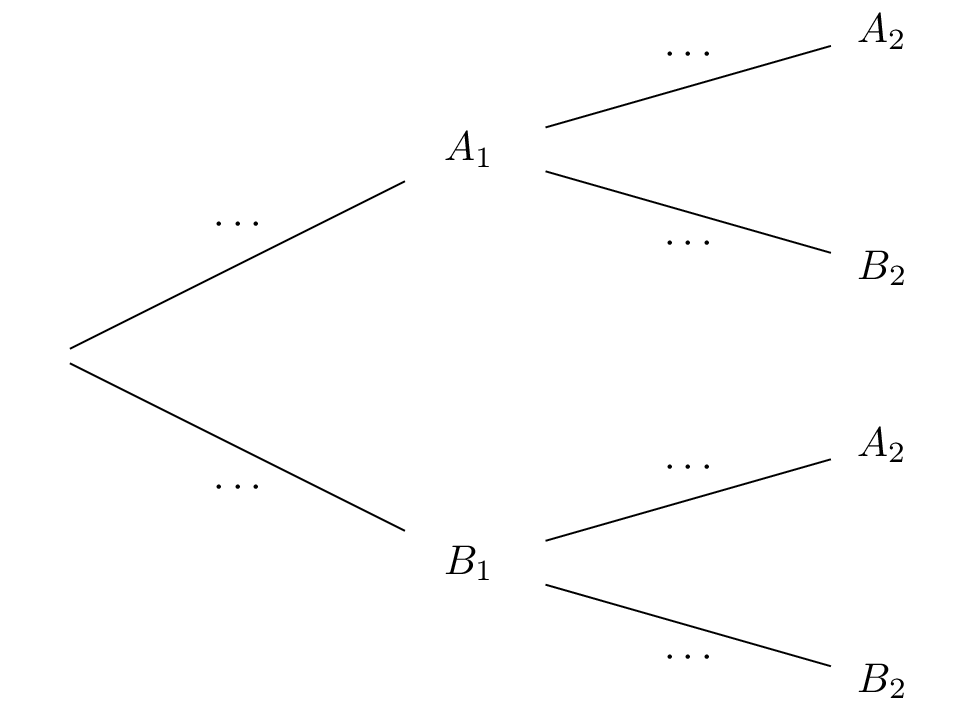Recopier et compléter l’arbre pondéré ci-dessous qui modélise la situation pour les deux premiers matins.

Correction

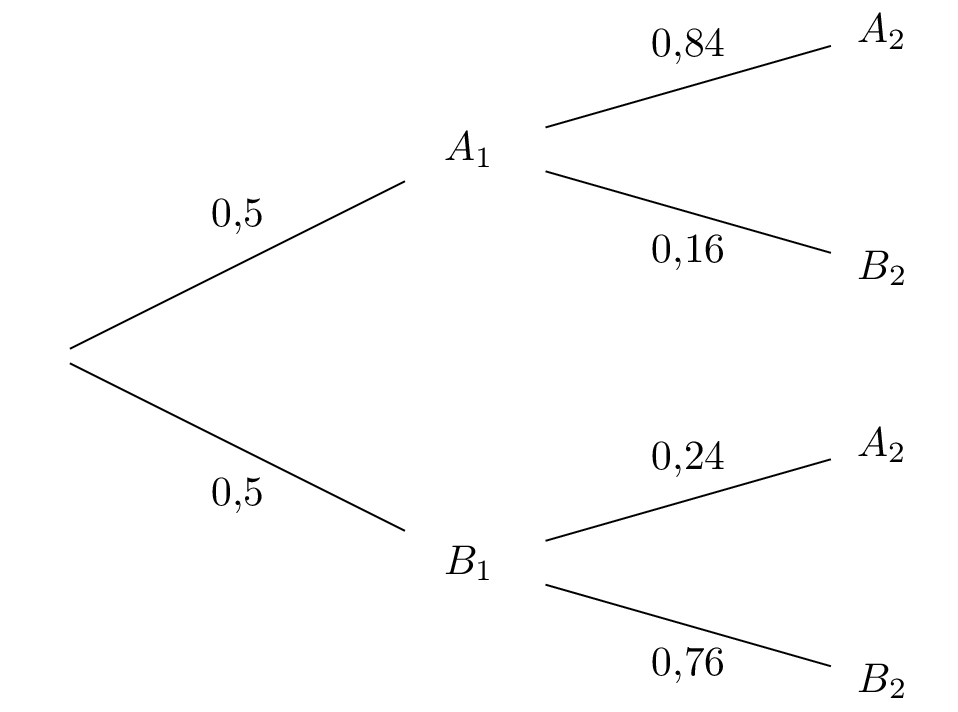
Question 2

Calculer $a_2$ .

Correction

D'après les hypothèses de l'énoncé, on sait que :

P\left(A_{2}\right)=a_{2}

Les évènements

A_1

B_1

forment une partition de l'univers. D'après la formule des probobilités totales on a :

P\left(A_{2}\right)=P\left(A_1\cap A_{2}\right)+P\left(B_1\cap A_{2}\right)

P\left(A_{2}\right)=P\left(A_1\right)\times P_{A_1}\left(A_{2}\right)+P\left(B_1\right)\times P_{B_1}\left(A_{2}\right)

P\left(A_{2}\right)=0,5\times 0,84+0,5\times 0,24

Ainsi :

a_{2}=0,54

Question 3

Le vélo se trouve au point $A$ le deuxième matin. Calculer la probabilité qu’il se soit trouvé au point $B$ le premier matin. La probabilité sera arrondie au millième .

Correction

On cherche cette fois à calculer une probabilité conditionnelle. On pourrait traduire la question de la manière suivante ;

{\color{blue}{\text{sachant}}}

que vélo se trouve au point

A

le deuxième matin, quelle est la probabilité qu’il se soit trouvé au point

B

le premier matin.
Ainsi :

P_{A_2} \left(B_{1}\right)=\frac{P\left(B_{1}\cap A_2\right)}{P\left(A_2\right)}

P_{A_2} \left(B_{1}\right)=\frac{0,5\times 0,24}{0,54}

P_{A_2} \left(B_{1}\right)\approx0,222

Question 4

Recopier et compléter l’arbre pondéré ci-dessous qui modélise la situation pour les nième et $\left(n+1\right)$ ^ièmematin matins.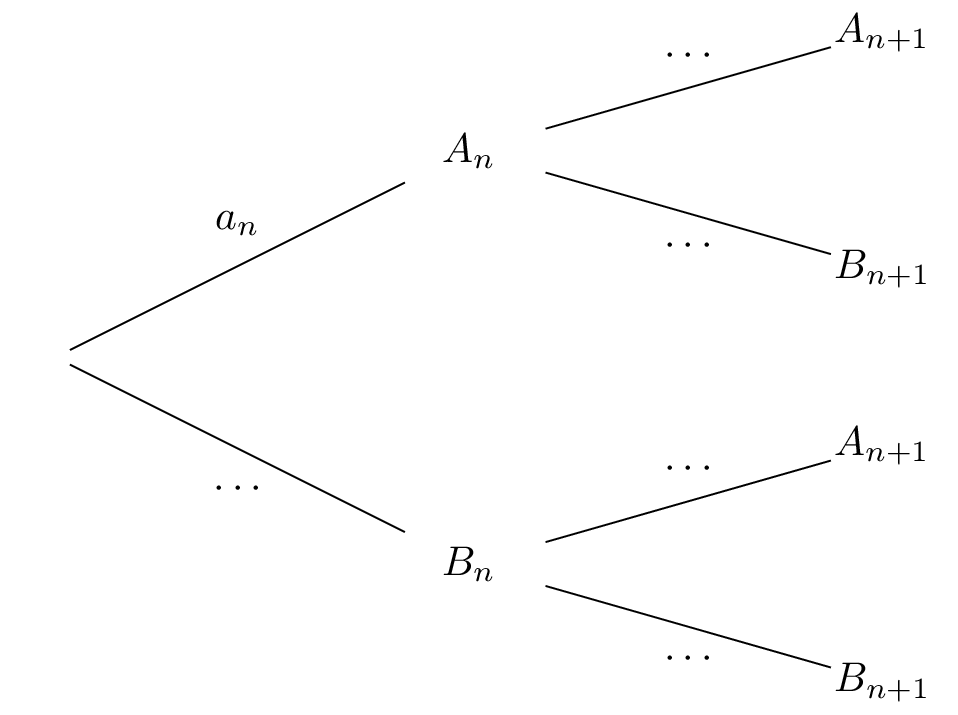

Correction

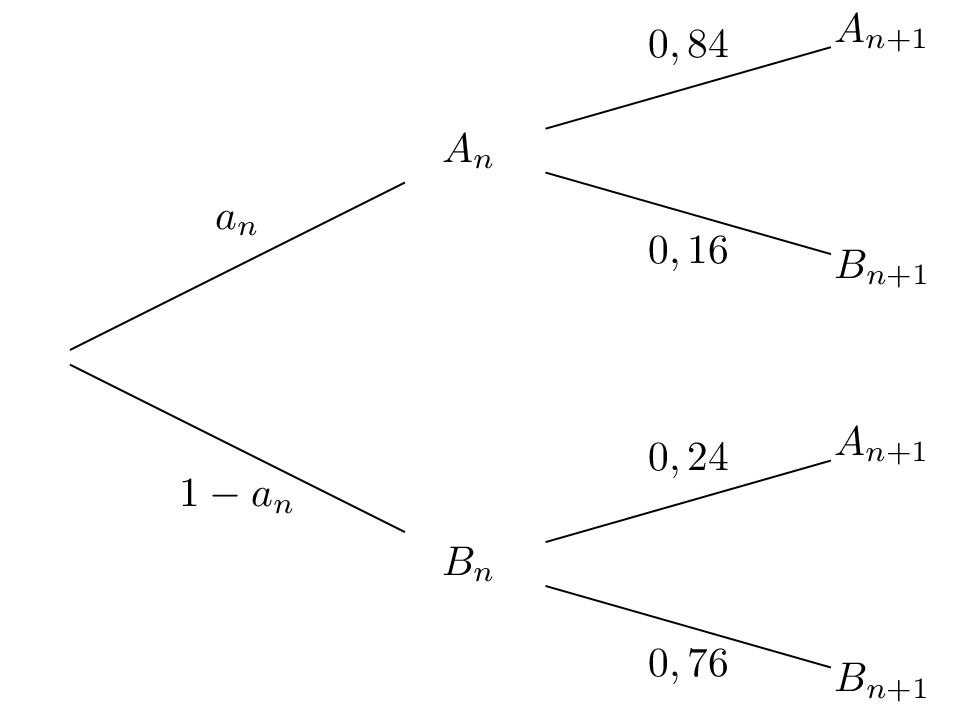
Question 5

Justifier que pour tout entier naturel non nul $n$ , $a_{n+1} = 0,6a_n +0,24$ .

Correction

D'après les hypothèses de l'énoncé, on sait que :

P\left(A_{n+1}\right)=a_{n+1}

Les évènements

A_n

B_n

forment une partition de l'univers. D'après la formule des probobilités totales on a :

P\left(A_{n+1}\right)=P\left(A_n\cap A_{n+1}\right)+P\left(B_n\cap A_{n+1}\right)

P\left(A_{n+1}\right)=P\left(A_n\right)\times P_{A_n}\left(A_{n+1}\right)+P\left(B_n\right)\times P_{B_n}\left(A_{n+1}\right)

P\left(A_{n+1}\right)=a_n\times 0,84+\left(1-a_n\right)\times 0,24

P\left(A_{n+1}\right)=0,84a_n+0,24-0,24a_n

P\left(A_{n+1}\right)=0,6a_n+0,24

Ainsi :

a_{n+1}=0,6a_n+0,24

Sur du long terme, la probabilité qu’un vélo soit à la station

A

est de

60\%

Question 6

Montrer par récurrence que, pour tout entier naturel non nul $n$ , $a_n = 0,6−0,1\times0,6^{n−1}$

Correction

On rappelle que que pour tout entier naturel non nul

n

a_{n+1} = 0,6a_n +0,24

.

Pour tout entier naturel

n

non nul, posons la propriété

P_{n} : a_n = 0,6−0,1\times0,6^{n−1}

$\purple{\text{Etape d'initialisation}}$
On sait que

a_{1} =0,5

et que

a_{1} =0,6−0,1\times0,6^{1−1}=0,5

.
La propriété

P_{1}

est vraie.
$\purple{\text{Etape d'hérédité}}$
On suppose qu'il existe un entier

k

tel que la propriété

P_{k}

soit vraie c'est-à-dire

a_k = 0,6−0,1\times0,6^{k−1}

et vérifions si la propriété est également vraie au rang

k+1

c'est-à-dire

a_{k+1} = 0,6−0,1\times0,6^{k}

Par hypothèse de récurrence :

a_k = 0,6−0,1\times0,6^{k−1}

, on multiplie par

0,6

de part et d'autre de l'égalité

0,6\times a_{k} =0,6\times \left(0,6−0,1\times0,6^{k−1}\right)

0,6\times a_{k} =0,6\times 0,6-0,1\times0,6^{k−1}\times 0,6

0,6\times a_{k} =0,6\times 0,6-0,1\times0,6^{k}

0,6\times a_{k} =0,36-0,1\times0,6^{k}

, on va maintenant additionner par

0,24

de part et d'autre de l'égalité (notre objectif est de faire apparaître dans le membre de gauche

a_{k+1}

)

0,6\times a_{k}+0,24 =0,36-0,1\times0,6^{k}+0,24

0,6\times a_{k}+0,24 =0,6-0,1\times0,6^{k}

u_{k+1} =0,6-0,1\times0,6^{k}

Ainsi la propriété

P_{k+1}

est vraie.
$\purple{\text{Conclusion}}$
Puisque la propriété

P_{1}

est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel

n

non nul, on a

P_{n}

vraie, c'est à dire que pour tout entier naturel

n

non nul, on a bien :

a_n = 0,6−0,1\times0,6^{n−1}

Question 7

Déterminer la limite de la suite $\left(a_n\right)$ et interpréter cette limite dans le contexte de l’exercice.

Correction

Si $-1<q<1$ alors $\lim\limits_{n\to +\infty } q^{n} =0$ .
Si $q >1$ alors $\lim\limits_{n\to +\infty } q^{n} =+\infty$ .

Comme

-1<0,6<1

alors :

\lim\limits_{n\to +\infty } 0,6^{n-1} =0

\lim\limits_{n\to +\infty } \left(-0,1\right)\times 0,6^{n-1} =0

\lim\limits_{n\to +\infty } 0,6-0,1\times 0,6^{n-1}=0,6

Ainsi :

\lim\limits_{n\to +\infty } a_{n} =0,6

Question 8

Déterminer le plus petit entier naturel $n$ tel que $a_n \ge 0,599$ et interpréter le résultat obtenu dans le contexte de l’exercice.

Correction

a_n \ge 0,599

équivaut successivement à :

0,6−0,1\times0,6^{n−1}\ge 0,599

−0,1\times0,6^{n−1}\ge 0,599-0,6

−0,1\times0,6^{n−1}\ge -0,001

0,6^{n−1}\le \frac{-0,001}{−0,1}

0,6^{n−1}\le 0,01

\ln \left(0,6\right)^{n-1} \le \ln \left(0,01\right)

\left(n-1\right)\ln \left(0,6\right)\le \ln \left(0,01\right)

\left(n-1\right)\ge \frac{\ln \left(0,01\right)}{\ln \left(0,6\right)}

On a divisé par

\ln \left(0,6\right)<0

, on change donc le sens de l'inégalité.

n\ge \frac{\ln \left(0,01\right)}{\ln \left(0,6\right)} +1

Or :

\frac{\ln \left(0,01\right)}{\ln \left(0,6\right)}+1 \approx 10,015

\;\;\;

. Il faut prendre le premier entier supérieur à

10,015

Il en résulte que :

n \ge 11

La probabilité que le vélo se trouve au point

A

est supérieure à

0,599

à partir du

11

^ième matin .

Epreuve d'enseignement de spécialité Session 19 Mai 2022 sujet 2 Exercice 1 : Probabilités conditionnelles et des SUITES - Exercice 1

Recopier et compléter l’arbre pondéré ci-dessous qui modélise la situation pour les deux premiers matins.

Calculer a2a_2a2​.

Le vélo se trouve au point AAA le deuxième matin. Calculer la probabilité qu’il se soit trouvé au point BBB le premier matin. La probabilité sera arrondie au millième .

Recopier et compléter l’arbre pondéré ci-dessous qui modélise la situation pour les nième et (n+1)\left(n+1\right)(n+1)ième matin matins.

Justifier que pour tout entier naturel non nul nnn, an+1=0,6an+0,24a_{n+1} = 0,6a_n +0,24an+1​=0,6an​+0,24.

Montrer par récurrence que, pour tout entier naturel non nul nnn, an=0,6−0,1×0,6n−1a_n = 0,6−0,1\times0,6^{n−1}an​=0,6−0,1×0,6n−1

Déterminer la limite de la suite (an)\left(a_n\right)(an​) et interpréter cette limite dans le contexte de l’exercice.

Déterminer le plus petit entier naturel nnn tel que an≥0,599a_n \ge 0,599an​≥0,599 et interpréter le résultat obtenu dans le contexte de l’exercice.

Calculer $a_2$ .

Le vélo se trouve au point $A$ le deuxième matin. Calculer la probabilité qu’il se soit trouvé au point $B$ le premier matin. La probabilité sera arrondie au millième .

Recopier et compléter l’arbre pondéré ci-dessous qui modélise la situation pour les nième et $\left(n+1\right)$ ^ièmematin matins.

Justifier que pour tout entier naturel non nul $n$ , $a_{n+1} = 0,6a_n +0,24$ .

Montrer par récurrence que, pour tout entier naturel non nul $n$ , $a_n = 0,6−0,1\times0,6^{n−1}$

Déterminer la limite de la suite $\left(a_n\right)$ et interpréter cette limite dans le contexte de l’exercice.

Déterminer le plus petit entier naturel $n$ tel que $a_n \ge 0,599$ et interpréter le résultat obtenu dans le contexte de l’exercice.