Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

Epreuve d'enseignement de spécialité Session 15 Mars 2021 sujet 2 Exercice 1 : Probabilités conditionnelles et loi binomiale - Exercice 1

20 min

Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.

\red{\text{Partie 1.}}

Dans un centre de traitement du courrier, une machine est équipée d’un lecteur optique automatique de reconnaissance de l’adresse postale.
Ce système de lecture permet de reconnaître convenablement

97\%

des adresses; le reste du courrier, que l’on qualifiera d’illisible pour la machine, est orienté vers un employé du centre chargé de lire les adresses.
Cette machine vient d’effectuer la lecture de neuf adresses. On note

X

la variable aléatoire qui donne le nombre d’adresses illisibles parmi ces neuf adresses.
On admet que

X

suit la loi binomiale de paramètres

n = 9

p = 0,03

Question 1

La probabilité qu’aucune des neuf adresses soit illisible est égale, au centième près, à :
$\bf{a.}$ $0$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $1$

$\bf{c.}$ $0,24$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $0,76$

Correction

\red{\text{la bonne réponse est d.}}

Soit

X

une variable aléatoire suivant la loi binomiale

\mathscr{B}\left(n;p\right)

alors, pour tout entier

k

compris entre

0

n

, on a :

P\left(X=k\right)=\left(\begin{array}{c} {n} \\ {k} \end{array}\right)p^{k} \left(1-p\right)^{n-k}

X

une variable aléatoire suivant la loi binomiale

\mathscr{B}\left(9;0,03\right)

.
Ainsi :

P\left(X=0\right)=\left(\begin{array}{c} {9} \\ {0} \end{array}\right)\times \left(0,03 \right)^{0} \times \left(1-0,03 \right)^{9-0}

P\left(X=0\right)=\left(\begin{array}{c} {9} \\ {0} \end{array}\right)\times \left(0,03 \right)^{0} \times \left(0,97 \right)^{9}

Finalement :

P\left(X=0\right) \approx 0,76

Question 2

La probabilité qu’exactement deux des neuf adresses soient illisibles pour la machine est :
$\bf{a.}$ $\left(\begin{array}{c} {9} \\ {2} \end{array}\right)\times 0,97^{2} \times 0,03^{7}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $\left(\begin{array}{c} {7} \\ {2} \end{array}\right)\times 0,97^{2} \times 0,03^{7}$

$\bf{c.}$ $\left(\begin{array}{c} {9} \\ {2} \end{array}\right)\times 0,97^{7} \times 0,03^{2}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $\left(\begin{array}{c} {7} \\ {2} \end{array}\right)\times 0,97^{7} \times 0,03^{2}$

Correction

\red{\text{la bonne réponse est c.}}

Soit

X

une variable aléatoire suivant la loi binomiale

\mathscr{B}\left(n;p\right)

alors, pour tout entier

k

compris entre

0

n

, on a :

P\left(X=k\right)=\left(\begin{array}{c} {n} \\ {k} \end{array}\right)p^{k} \left(1-p\right)^{n-k}

X

une variable aléatoire suivant la loi binomiale

\mathscr{B}\left(9;0,03\right)

.
Ainsi :

P\left(X=2\right)=\left(\begin{array}{c} {9} \\ {2} \end{array}\right)\times \left(0,03 \right)^{2} \times \left(1-0,03 \right)^{9-2}

Finalement :

P\left(X=2\right)=\left(\begin{array}{c} {9} \\ {2} \end{array}\right)\times 0,97^{7} \times 0,03^{2}

Question 3

La probabilité qu’au moins une des neuf adresses soit illisible pour la machine est :
$\bf{a.}$ $P\left(X<1\right)$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $P\left(X\le 1\right)$

$\bf{c.}$ $P\left(X\ge 2\right)$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $1-P\left(X=0\right)$

Correction

\red{\text{la bonne réponse est d.}}

On doit calculer :

P\left(X\ge 1\right)

.
Or

P\left(X\ge 1\right)=1-P\left(X=0\right)

Question 4

\red{\text{Partie 2.}}

Une urne contient

5

boules vertes et

3

boules blanches, indiscernables au toucher.
On tire au hasard successivement et sans remise deux boules de l’urne.
On considère les évènements suivants :

V1 : « la première boule tirée est verte »;

B1 : « la première boule tirée est blanche »;

V2 : « la seconde boule tirée est verte »;

B2 : « la seconde boule tirée est blanche ».

La probabilité de $V_2$ sachant que $V_1$ est réalisé, notée $P_{V_{1} } \left(V_{2} \right)$ est égale à :
$\bf{a.}$ $\frac{5}{8}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $\frac{4}{7}$

$\bf{c.}$ $\frac{5}{14}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $\frac{3}{7}$

Correction

\red{\text{la bonne réponse est b.}}

On commence par construire l'arbre pondéré traduisant l'énoncé.

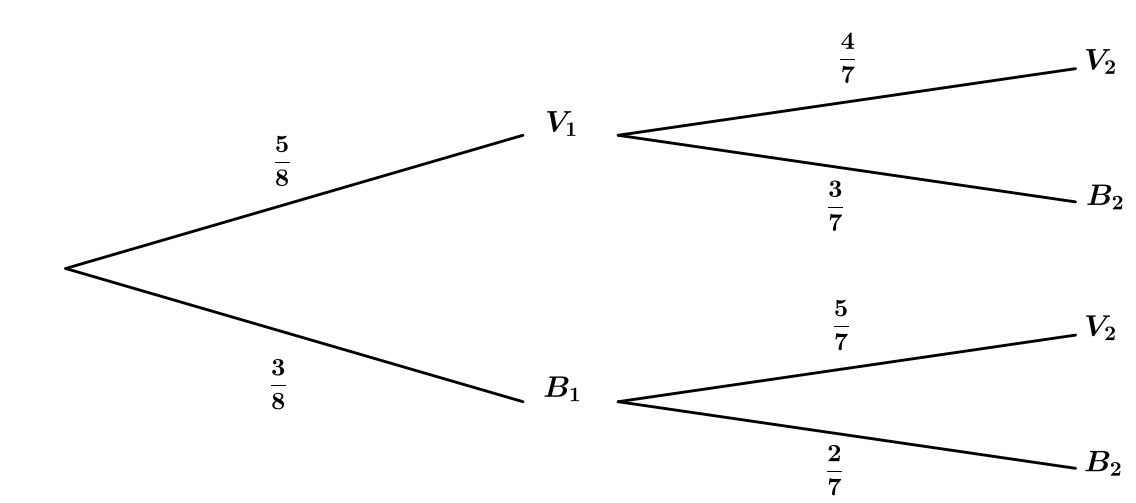
Par simple lecture de l'arbre pondéré, on lit alors que :

P_{V_{1} } \left(V_{2} \right)=\frac{4}{7}

Question 5

La probabilité de l’évènement $V_2$ est égale à :
$\bf{a.}$ $\frac{5}{8}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{b.}$ $\frac{5}{7}$

$\bf{c.}$ $\frac{3}{28}$ $\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ $\bf{d.}$ $\frac{9}{7}$

Correction

V_{1}

B_{1}

forment une partition de l'univers.
D'après la formule des probabilités totales on a :

P\left(V_{2} \right)=P\left(V_{1} \cap V_{2} \right)+P\left(B_{1} \cap V_{2} \right)

P\left(V_{2} \right)=P\left(V_{1} \right)\times P_{V_{1} } \left(V_{2} \right)+P\left(B_{1} \right)\times P_{B_{1} } \left(V_{2} \right)

P\left(V_{2} \right)=\frac{5}{8} \times \frac{4}{7} +\frac{3}{8} \times \frac{5}{7}

P\left(V_{2} \right)=\frac{20}{56} +\frac{15}{56}

P\left(V_{2} \right)=\frac{35}{56}

Ainsi :

P\left(V_{2} \right)=\frac{5}{8}