Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Epreuve d'enseignement de spécialité Session 15 Mars 2021 sujet 1 Exercice 1 : Probabilités conditionnelles et loi binomiale - Exercice 1
25 min
45
Dans une école de statistique, après étude des dossiers des candidats, le recrutement se fait de deux façons :
des candidats sont sélectionnés sur dossier. Ces candidats doivent ensuite passer un oral à l’issue duquel d’entre eux sont finalement admis à l’école. Les candidats n’ayant pas été sélectionnés sur dossier passent une épreuve écrite à l’issue de laquelle d’entre eux sont admis à l’école.
On choisit au hasard un candidat à ce concours de recrutement. On notera :
l’évènement « le candidat a été sélectionné sur dossier »; l’évènement « le candidat a été admis à l’école »;
On choisit au hasard un candidat à ce concours de recrutement. On notera :
Question 1
Traduire la situation par un arbre pondéré.
Correction
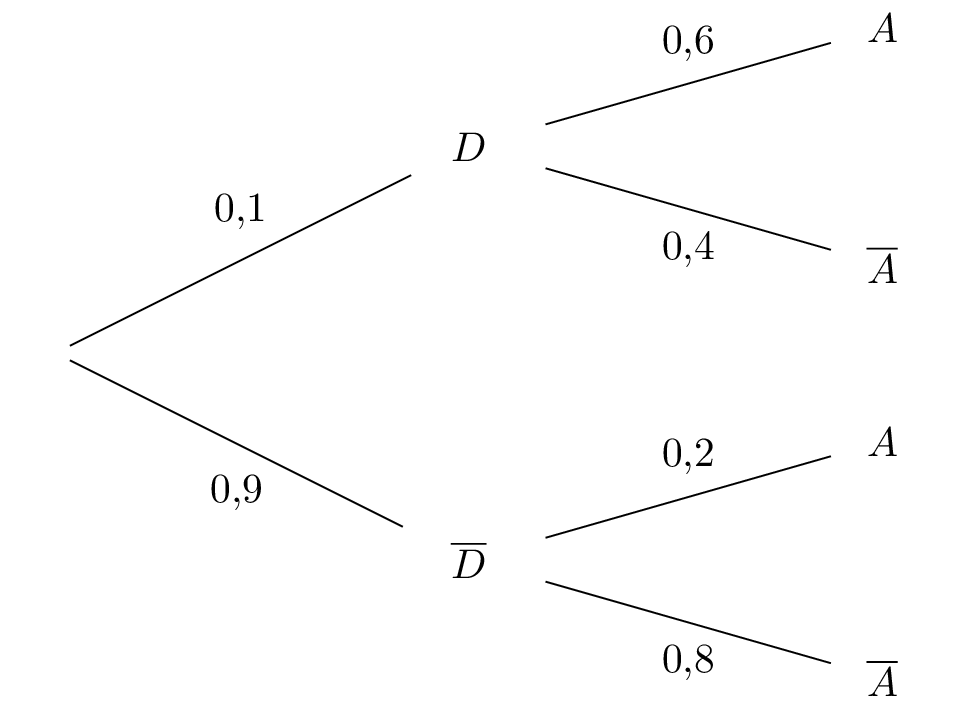
Question 2
Calculer la probabilité que le candidat soit sélectionné sur dossier et admis à l’école.
Correction

Ainsi :
La probabilité que le candidat soit sélectionné sur dossier et admis à l’école est de .
Question 3
Montrer que la probabilité de l’évènement est égale à .
Correction

D'après la formule des probabilités totales, on a :
équivaut successivement à
Ainsi :
La probabilité de l’évènement est égale à
Question 4
On choisit au hasard un candidat admis à l’école. Quelle est la probabilité que son dossier n’ait pas été sélectionné ?
Correction

- On note la probabilité d’avoir l’événement sachant que l’événement est réalisé. On a alors la relation suivante :
-
Ainsi :
Ainsi :
Question 5
On admet que la probabilité pour un candidat d’être admis à l’école est égale à . On considère un échantillon de sept candidats choisis au hasard, en assimilant ce choix à un tirage au sort avec remise.
On désigne par la variable aléatoire dénombrant les candidats admis à l’école parmi les sept tirés au sort.
On admet que la variable aléatoire suit une loi binomiale. Quels sont les paramètres de cette loi ?
Correction
On considère l'expérience ci-dessous
On appelle « le candidat est admis à l’école » avec la probabilité On appelle « le candidat n'est pas admis à l’école » avec la probabilité On répète fois de suite cette expérience de Bernoulli de .
On est donc en présence
est la variable aléatoire dénombrant les candidats admis à l’école parmi les sept tirés au sort.
suit la loi binomiale de paramètre et
On note alors suit la loi binomiale
On est donc en présence
est la variable aléatoire dénombrant les candidats admis à l’école parmi les sept tirés au sort.
suit la loi binomiale de paramètre et
On note alors suit la loi binomiale
Question 6
Calculer la probabilité qu’un seul des sept candidats tirés au sort soit admis à l’école. On donnera une réponse arrondie au centième.
Correction
Il nous faut calculer
Avec la formule du cours
En utilisant les fonctionnalités de la calculatrice
on tape pour
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Texas" pour plus de détails)
2nd - DISTR -- puis choisir BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(7, , 2) puis taper sur enter et on obtient :
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp
on tape pour :
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Casio" pour plus de détails)
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
puis taper sur EXE et on obtient :
Avec la formule du cours
Soit une variable aléatoire suivant la loi binomiale alors, pour tout entier compris entre et , on a :
Ainsi : En utilisant les fonctionnalités de la calculatrice
on tape pour
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Texas" pour plus de détails)
2nd - DISTR -- puis choisir BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(7, , 2) puis taper sur enter et on obtient :
arrondi à près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp
on tape pour :
(tu peux regarder la vidéo "Utiliser la loi binomiale avec une Casio" pour plus de détails)
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
On remplit le tableau de la manière qui suit :
D.P. Binomiale
Data Variable
: valeur de
Numtrial : valeur de
: valeur de
Data Variable
: valeur de
Numtrial : valeur de
: valeur de
puis taper sur EXE et on obtient :
arrondi à près.
Question 7
Calculer la probabilité qu’au moins deux des sept candidats tirés au sort soient admis à cette école. On donnera une réponse arrondie au centième.
Correction
Nous devons calculer
Or :
La valeur de s'obtient grâce à la calculatrice.
En effet, pour obtenir , il faut utiliser BinomFrep avec une texas ou alors Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR avec une casio.
D'où :
Finalement :
Il vient alors que :
Or :
La valeur de s'obtient grâce à la calculatrice.
En effet, pour obtenir , il faut utiliser BinomFrep avec une texas ou alors Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR avec une casio.
D'où :
Finalement :
Il vient alors que :
Question 8
Un lycée présente candidats au recrutement dans cette école, où est un entier naturel non nul. On admet que la probabilité pour un candidat quelconque du lycée d’être admis à l’école est égale à et que les résultats des candidats sont indépendants les uns des autres.
Donner l’expression, en fonction de , de la probabilité qu’aucun candidat issu de ce lycée ne soit admis à l’école
Correction
On introduit une nouvelle variable aléatoire dénombrant les candidats admis à l’école parmi les tirés au sort.
On note alors suit la loi binomiale
Or : et .
Ainsi :
On note alors suit la loi binomiale
Soit une variable aléatoire suivant la loi binomiale alors, pour tout entier compris entre et , on a :
Nous voulons donc calculer .Or : et .
Ainsi :
Question 9
À partir de quelle valeur de l’entier la probabilité qu’au moins un élève de ce lycée soit admis à l’école est-elle supérieure ou égale à ?
Correction
Il nous faut calculer :
Or : et comme alors .
Ainsi :
On a divisé par , on change donc le sens de l'inégalité.
Or : Il faut prendre le premier entier supérieur à
Il en résulte que :
Or : et comme alors .
Ainsi :
On a divisé par , on change donc le sens de l'inégalité.
Or : Il faut prendre le premier entier supérieur à
Il en résulte que :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.