Succession d'épreuves indépendantes et loi binomiale

Epreuve d'enseignement de spécialité Amérique du Nord Mai 2021 Exercice 3 : Probabilités conditionnelles et loi binomiale - Exercice 1

20 min
40
Un laboratoire pharmaceutique vient d’élaborer un nouveau test anti-dopage.
Partie A\purple{\text{Partie A}}
Une étude sur ce nouveau test donne les résultats suivants :
  • si un athlète est dopé, la probabilité que le résultat du test soit positif est 0,980,98 (sensibilité du test);
  • si un athlète n’est pas dopé, la probabilité que le résultat du test soit négatif est 0,9950,995
    • On fait subir le test à un athlète sélectionné au hasard au sein des participants à une compétition d’athlétisme.
    On note DD l’évènement « l’athlète est dopé » et TT l’évènement « le test est positif ».
    On admet que la probabilité de l’évènement DD est égale à 0,080,08.
    Question 1

    Traduire la situation sous la forme d’un arbre pondéré .

    Correction
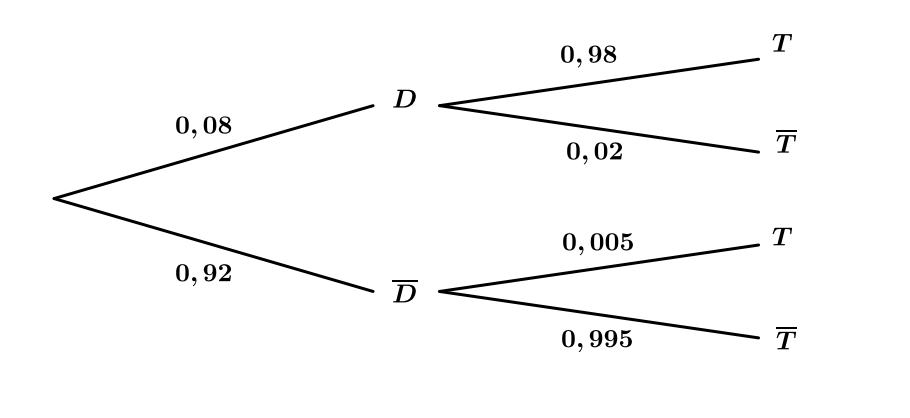
    Question 2

    Démontrer que P(T)=0,083P\left(T\right ) = 0,083.

    Correction
    Les évènements DD et D‾\overline{D} forment une partition de l'univers.
    D'après la formule des probabilités totales, on a :
    P(T)=P(D∩T)+P(D‾∩T)P\left(T\right)=P\left(D\cap T\right)+P\left(\overline{D}\cap T\right)
    P(T)=P(D)×PD(T)+P(D‾)×PD‾(T)P\left(T\right)=P\left(D\right)\times P_{D} \left(T\right)+P\left(\overline{D}\right)\times P_{\overline{D}} \left(T\right)
    P(T)=0,08×0,98+0,92×0,005P\left(T\right)=0,08\times 0,98+0,92\times 0,005
    Ainsi :
    P(T)=0,083P\left(T\right)=0,083

    Question 3

    Sachant qu’un athlète présente un test positif, quelle est la probabilité qu’il soit dopé ?

    Correction
    Il s'agit d'une probabilité conditionnelle.
      On note PB(A)P_{B} \left(A\right) la probabilité d’avoir l’événement AA sachant que l’événement BB est réalisé. On a alors la relation suivante :
    • PB(A)=P(A∩B)P(B)P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}
    Ainsi :
    PT(D)=P(D∩T)P(T)P_{T} \left(D\right)=\frac{P\left(D\cap T\right)}{P\left(T\right)}
    PT(D)=P(D)×PD(T)P(T)P_{T} \left(D\right)=\frac{P\left(D\right)\times P_{D} \left(T\right)}{P\left(T\right)}
    PT(D)=0,08×0,980,083P_{T} \left(D\right)=\frac{0,08\times 0,98}{0,083}
    Ainsi :
    PT(D)≈0,945P_{T} \left(D\right)\approx0,945

    Question 4

    Le laboratoire décide de commercialiser le test si la probabilité de l’évènement « un athlète présentant un test positif est dopé » est supérieure ou égale à 0,950,95.
    Le test proposé par le laboratoire sera-t-il commercialisé? Justifier.

    Correction
    D’après la question précédente 0,945<0,950,945 < 0,95.
    Le test ne sera pas commercialisé.
    Question 5
    Partie B\purple{\text{Partie B}}
    Dans une compétition sportive, on admet que la probabilité qu’un athlète contrôlé présente un test positif est 0,1030,103.
    Pour les questions\red{\text{Pour les questions}} 5\red{5} , 6\red{6} et\red{\text{et}} 7\red{7} , on suppose que les organisateurs décident de contrôler 55 athlètes au hasard parmi les athlètes de cette compétition.
    On note XX la variable aléatoire égale au nombre d’athlètes présentant un test positif parmi les 55 athlètes contrôlés.

    Donner la loi suivie par la variable aléatoire XX. Préciser ses paramètres.

    Correction
    Reˊdaction type pour la loi binomiale :\purple{\text{Rédaction type pour la loi binomiale :}}
    On considère l'expérience ci-dessous aˋ deux issues :\red{\text{à deux issues :}}
  • On appelle succeˋs\red{\text{succès}} « l'athlète contrôlé présente un test positif » avec la probabilité p=0,103p=0,103
  • On appelle eˊchec\red{\text{échec}} « l'athlète contrôlé ne présente pas un test positif » avec la probabilité 1−p=0,8971-p=0,897
    • On répète 55 fois de suite cette expérience de Bernoulli de façon indeˊpendante\red{\text{façon indépendante}}.
    On est donc en présence d’un scheˊma de Bernoulli.\red{\text{d'un schéma de Bernoulli.}}
    XX est la variable aléatoire qui associe le nombre d’athlètes présentant un test positif parmi les 55 athlètes contrôlés.
    XX suit la loi binomiale de paramètre n=5n=5 et p=0,103p=0,103
    On note alors XX suit la loi binomiale B(5;0,103)\mathscr{B}\left(5;0,103\right)

    Question 6

    Calculer l’espérance E(X)E\left(X\right) et interpréter le résultat dans le contexte de l’exercice.

    Correction
    XX est une variable aléatoire qui suit une loi binomiale B(n,p)B\left(n, p\right), alors l’espérance mathématique E(X)E\left(X\right), la variance V(X)V\left(X\right) et l’écart type σ(X)\sigma\left(X\right) sont égales à :
  • E(X)=n×pE\left(X\right)=n\times p
    • Soit XX suit la loi binomiale B(5;0,103)\mathscr{B}\left(5;0,103\right)
    Ainsi :
    E(X)=5×0,103E\left(X\right)=5\times 0,103 donc
    E(X)=0,515E\left(X\right)=0,515

    En moyenne, sur un grand nombre de contrôles, il y aura un athlète sur 1010 contrôlé positif. ( nous n'avons pas pris 0,5150,515 mais 11 car on peut pas prendre la moitié d'un homme ).
    Question 7

    Quelle est la probabilité qu’au moins un des 55 athlètes contrôlés présente un test positif ?

    Correction
    On doit calculer : P(X≥1)P\left(X\ge 1\right).
    Or P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    Pour le calcul de P(X=0)P\left(X=0\right) :
    En appliquant la formule du cours :\red{\text{En appliquant la formule du cours :}}
    On rappelle que XX suit la loi binomiale B(5;0,103)\mathscr{B}\left(5;0,103\right)
    Soit XX une variable aléatoire suivant la loi binomiale B(n;p)\mathscr{B}\left(n;p\right) alors, pour tout entier kk compris entre 00 et nn, on a :
  • P(X=k)=(nk)pk(1−p)n−kP\left(X=k\right)=\left(\begin{array}{c} {n} \\ {k} \end{array}\right)p^{k} \left(1-p\right)^{n-k}
    • Ainsi :
    P(X=0)=(50)×(0,103)2×(1−0,103)5−0≈0,581P\left(X=0\right)=\left(\begin{array}{c} {5} \\ {0} \end{array}\right)\times \left(0,103 \right)^{2} \times \left(1-0,103 \right)^{5-0} \approx 0,581

    Finalement : P(X≥1)=1−P(X=0)≈1−0,581P\left(X\ge 1\right)=1-P\left(X=0\right)\approx1-0,581 d'où P(X≥1)≈0,419P\left(X\ge 1\right)\approx0,419
    Avec une Texas :\red{\text{Avec une Texas :}} pour P(X=0)P\left(X=0\right) on tape :
    (tu peux regarder la fiche "Utiliser la loi binomiale avec une Texas" pour plus de détails)
    2nd - DISTR -- puis choisir
    BinomFdp(valeur de n, valeur de p, valeur de k) c'est-à-dire ici BinomFdp(5, 0.1030.103 , 0) puis on tape sur enter et on obtient :
    P(X=0)≈0,581P\left(X=0\right)\approx 0,581
    arrondi à 10−310^{-3} près.
    Pour certaines versions de Texas, on aura BinomPdf au lieu de BinomFdp.
    Enfin : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    Soit : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    D'où :
    P(X≥1)≈1−0,581≈0,419P\left(X\ge 1\right)\approx 1-0,581 \approx 0,419

    Avec une calculatrice Casio Graph 35+ ou modeˋle supeˊrieur :\red{\text{Avec une calculatrice Casio Graph 35+ ou modèle supérieur :}} pour P(X=0)P\left(X=0\right) :
    (tu peux regarder la fiche "Utiliser la loi binomiale avec une Casio" pour plus de détails)
    Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR.
    On remplit le tableau de la manière qui suit :
    D.P. Binomiale
    Data Variable
    xx : 00 Valeur de kk
    Numtrial : 55 Valeur de nn
    pp : 0,1030,103 Valeur de pp

    puis on tape sur EXE et on obtient :
    P(X=0)≈0,581P\left(X=0\right)\approx 0,581
    arrondi à 10−310^{-3} près.
    Enfin : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    Soit : P(X≥1)=1−P(X=0)P\left(X\ge 1\right)=1-P\left(X=0\right)
    D'où :
    P(X≥1)≈1−0,581≈0,419P\left(X\ge 1\right)\approx 1-0,581 \approx 0,419

    Question 8

    Combien d’athlètes faut-il contrôler au minimum pour que la probabilité de l’évènement « au moins un athlète contrôlé présente un test positif » soit supérieure ou égale à 0,750,75 ? Justifier.

    Correction
    Pour cette question, le nombre d'athlète n'est pas connu.
    Nous allons introduire une nouvelle loi binomiale donc les paramètres seront nn et 0,1030,103.
    On notera alors YY suit la loi binomiale B(n;0,103)\mathscr{B}\left(n;0,103\right)
    Nous voulons donc déterminer la valeur de nn vérifiant : P(Y≥1)≥0,75P\left(Y\ge 1\right)\ge 0,75 qui s'écrit également : 1−P(Y=0)≥0,751-P\left(Y=0\right)\ge 0,75
    Soit XX une variable aléatoire suivant la loi binomiale B(n;p)\mathscr{B}\left(n;p\right) alors, pour tout entier kk compris entre 00 et nn, on a :
  • P(X=k)=(nk)pk(1−p)n−kP\left(X=k\right)=\left(\begin{array}{c} {n} \\ {k} \end{array}\right)p^{k} \left(1-p\right)^{n-k}
    • Nous voulons donc calculer, en premier lieu : P(Y=0)P\left(Y=0\right) .
    P(Y=0)=(n0)(0,103)0(1−0,103)n−0P\left(Y=0\right)=\left(\begin{array}{c} {n} \\ {0} \end{array}\right)\left(0,103\right)^{0} \left(1-0,103\right)^{n-0}
    P(Y=0)=(n0)(0,103)0(0,897)nP\left(Y=0\right)=\left(\begin{array}{c} {n} \\ {0} \end{array}\right)\left(0,103\right)^{0} \left(0,897\right)^{n}
    Or : (n0)=1\left(\begin{array}{c} {n} \\ {0} \end{array}\right)=1 et (0,103)0=1\left(0,103\right)^{0}=1 .
    Ainsi :
    P(Y=0)=(0,897)nP\left(Y=0\right)= \left(0,897\right)^{n}

    Il vient alors que :
    1−P(Y=0)≥0,751-P\left(Y=0\right)\ge 0,75 équivaut successivement à :
    1−(0,897)n≥0,751-\left(0,897\right)^{n}\ge 0,75
    −(0,897)n≥0,75−1-\left(0,897\right)^{n} \ge 0,75-1
    −(0,897)n≥−0,25-\left(0,897\right)^{n} \ge -0,25
    (0,897)n≤0,25\left(0,897\right)^{n} \le 0,25
    ln⁡(0,897)n≤ln⁡(0,25)\ln \left(0,897\right)^{n} \le \ln \left(0,25\right)
    nln⁡(0,897)≤ln⁡(0,25)n\ln \left(0,897\right)\le \ln \left(0,25\right)
    n≥ln⁡(0,25)ln⁡(0,897)n\ge \frac{\ln \left(0,25\right)}{\ln \left(0,897\right)} On a divisé par ln⁡(0,897)<0\ln \left(0,897\right)<0, on change donc le sens de l'inégalité.
    Or : ln⁡(0,25)ln⁡(0,897)≈12,75\frac{\ln \left(0,25\right)}{\ln \left(0,897\right)} \approx 12,75       \;\;\; Il faut prendre le premier entier supérieur à 12,7512,75
    Il en résulte que :
    n≥13n \ge 13

    Il faut donc contrôler 1313 athlètes en moyenne pour que la probabilité de l’évènement « au moins un athlète contrôlé présente un test positif » soit supérieure ou égale à 0,750,75 .