Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Rappels de première spécialité : espérance et écart type - Exercice 2
10 min
15
Une urne contient boules indiscernables au toucher : bleues et rouges. On extrait l'une après l'autre, sans remise, deux boules de l'urne.
A chaque issue, on associe le nombre de boules bleues obtenues. On définit ainsi une variable aléatoire .
A chaque issue, on associe le nombre de boules bleues obtenues. On définit ainsi une variable aléatoire .
Question 1
Traduire l'énoncé à l'aide d'un arbre.
Correction
On note :
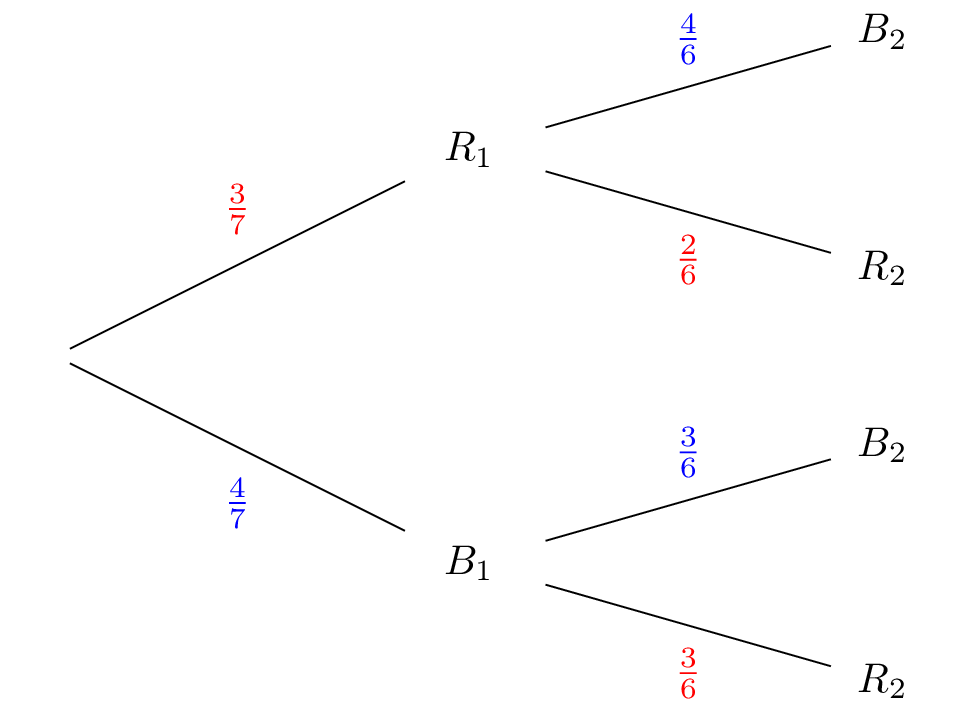
- la première boule tirée est de couleur rouge.
- la première boule tirée est de couleur bleue.
- la deuxième boule tirée est de couleur rouge.
- la deuxième boule tirée est de couleur bleue.

Question 2
Calculer
Correction
signifie que l'on a tiré aucune boule bleue lors des deux tirages.
Cela signifie que lors du premier tirage on tire et lors du deuxième tirage on tire .
Nous pouvons écrire alors que :
Cela signifie que lors du premier tirage on tire et lors du deuxième tirage on tire .
Nous pouvons écrire alors que :
Question 3
Définir la loi de probabilité de .
Correction
Il nous faut calculer maintenant et .
D'une part :
D'autre part :
Nous allons maintenant dresser la loi de probabilité de .

D'une part :
D'autre part :
Nous allons maintenant dresser la loi de probabilité de .

Question 4
Calculer l'espérance et l'écart type de .
Correction

On appelle l’espérance mathématique de la variable , la quantité notée définie par :
D'une part : Calculons l'espérance ( on peut également considérer que l'espérance est la moyenne )La formule de l'écart type est obtenue après avoir calculer la variance .
Les formules de la variance et de l'écart type sont données ci-dessous :
Les formules de la variance et de l'écart type sont données ci-dessous :
à près.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.