🔴  Lives #BAC2024

À partir du 12 mai, révise le bac avec nous sur YouTube tous les soirs à 19h30 ! Découvrir la chaîne →

Sommes de deux variables

Exercices types : 11ère partie - Exercice 1

25 min
45
Dans un examen, un exercice est constitué de deux questions Q1 et Q2.
Chaque question est notée sur un point. Une réponse correcte rapporte un point ; une réponse incorrecte, incomplète ou une absence de réponse rapporte zéro point.
On considère que :
  • Un candidat pris au hasard a une probabilité 0,80,8 de répondre correctement à la question Q1.
  • Si le candidat répond correctement à Q1, il a une probabilité 0,60,6 de répondre correctement à Q2 ; s’il ne répond pas correctement à Q1, il a une probabilité 0,10,1 de répondre correctement à Q2.
    • On prend un candidat au hasard et on note :
  • AA l’événement : « le candidat répond correctement à la question Q1 » ;
  • BB l’événement : « le candidat répond correctement à la question Q2 ».
    • On note A‾\overline{A} et B‾\overline{B} les événements contraires de AA et de BB.
    Question 1

    Recopier et compléter les pointillés de l’arbre pondéré ci-dessous.

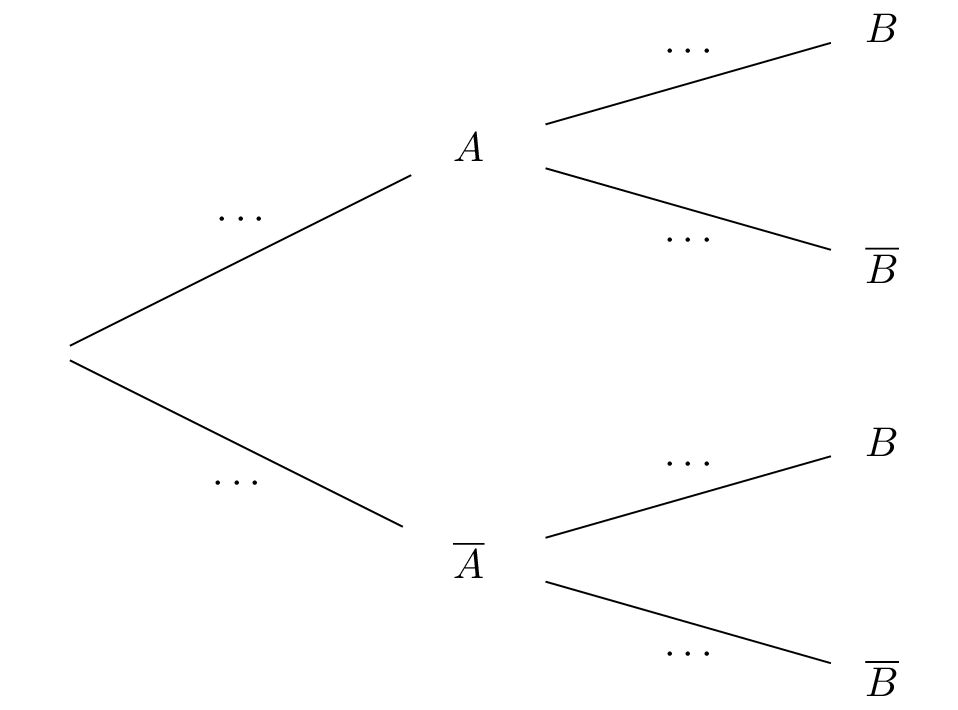
    Correction
    D'après l'énoncé, on complète l'arbre pondéré comme suit.
    Question 2

    Calculer la probabilité que le candidat réponde correctement aux deux questions Q1 et Q2 .

    Correction
    Calculer la probabilité que le candidat réponde correctement aux deux questions Q1 et Q2 se traduit par p(A∩B)p\left(A\cap B\right) .
    Il vient alors que :
    P(A∩B)=P(A)×PA(B)P\left(A\cap B\right)=P\left(A\right)\times P_{A} \left(B\right)
    P(A∩B)=0,8×0,6P\left(A\cap B\right)=0,8\times 0,6
    P(A∩B)=0,48P\left(A\cap B\right)=0,48

    Question 3

    Calculer la probabilité que le candidat réponde correctement à la question Q2.

    Correction
    Il nous faut calculer P(B)P\left(B\right) .
    AA et A‾\overline{A} forment une partition de l'univers.
    D'après la formule des probabilités totales on a :
    P(B)=P(A∩B)+P(A‾∩B)P\left(B\right)=P\left(A\cap B\right)+P\left(\overline{A}\cap B\right)
    P(B)=P(A)×PA(B)+P(A‾)×PA‾(B)P\left(B\right)=P\left(A\right)\times P_{A} \left(B\right)+P\left(\overline{A}\right)\times P_{\overline{A}} \left(B\right)
    Soit : P(B)=0,8×0,6+0,2×0,1P\left(B\right)=0,8\times 0,6 +0,2\times 0,1
    Ainsi :
    P(B)=0,5P\left(B\right)=0,5

    Question 4

    On note :
  • X1X_1 la variable aléatoire qui, à un candidat, associe sa note à la question Q1 ;
  • X2X_2 la variable aléatoire qui, à un candidat, associe sa note à la question Q2 ;
  • XX la variable aléatoire qui, à un candidat, associe sa note à l’exercice, c’est-à-dire X=X1+X2X=X_1+X_2 .
    • Déterminer l’espérance de X1X_1 et de X2X_2. En déduire l’espérance de XX. Donner une interprétation de l’espérance de XX dans le contexte de l’exercice.

    Correction
    D'après l'énoncé de l'exercice, la probabilité que le candidat réponde correctement à la question Q1 est égale à 0,80,8 . Ainsi :
    E(X1)=0,8E\left(X_1\right)=0,8

    D'après la question 33, la probabilité que le candidat réponde correctement à la question Q2 est égale à 0,50,5 . Ainsi :
    E(X2)=0,5E\left(X_2\right)=0,5
    Application de la linéarité de l’espérance
      Pour toutes variables aléatoires XX et YY, et pour tous nombres réels aa et bb :
  • E(X+Y)=E(X)+E(Y)E\left(X+Y\right)=E\left(X\right)+E\left(Y\right)
  • E(aX)=aE(X)E\left(aX\right)=aE\left(X\right)
  • E(X+b)=E(X)+bE\left(X+b\right)=E\left(X\right)+b
  • E(aX+b)=aE(X)+bE\left(aX+b\right)=aE\left(X\right)+b
    • Ainsi :
    E(X1+X2)=E(X1)+E(X2)E\left(X_1+X_2\right)=E\left(X_1\right)+E\left(X_2\right)
    E(X1+X2)=0,8+0,5E\left(X_1+X_2\right)=0,8+0,5
    Ainsi :
    E(X1+X2)=1,3E\left(X_1+X_2\right)=1,3

    Question 5

    On souhaite déterminer la variance de XX.
    Déterminer P(X=0)P\left(X=0\right) et P(X=2)P\left(X=2\right). En déduire P(X=1)P\left(X=1\right).

    Correction
  • P(X=0)P\left(X=0\right) signifie que le candidat n'a pas répondu correctement ni à la question 11 ni à la question 22.
    • Il en résulte donc que :
    P(X=0)=P(A‾∩B‾)P\left(X=0\right)=P\left(\overline{A}\cap \overline{B}\right)
    P(A‾∩B‾)=P(A‾)×PA‾(B‾)P\left(\overline{A}\cap \overline{B}\right)=P\left(\overline{A}\right)\times P_{\overline{A}} \left(\overline{B}\right)
    P(A‾∩B‾)=0,2×0,9P\left(\overline{A}\cap \overline{B}\right)=0,2\times 0,9
    P(A‾∩B‾)=0,18P\left(\overline{A}\cap \overline{B}\right)=0,18
    ainsi P(X=0)=0,18P\left(X=0\right)=0,18
  • P(X=2)P\left(X=2\right) signifie que le candidat a répondu correctement à la question 11 et correctement à la question 22.
    • Il en résulte donc que :
    P(X=2)=P(A∩B)P\left(X=2\right)=P\left(A\cap B\right)
    Nous avons vu à la question 11 que
    P(A∩B)=0,48P\left(A\cap B\right)=0,48
    ainsi P(X=2)=0,48P\left(X=2\right)=0,48
    • La somme des probabilités de toutes les issues est égale à 1.
    Il en résulte donc que :
    P(X=0)+P(X=1)+P(X=2)=1P\left(X=0\right)+P\left(X=1\right)+P\left(X=2\right)=1
    D'où :
    P(X=1)=1−P(X=0)−P(X=2)P\left(X=1\right)=1-P\left(X=0\right)-P\left(X=2\right)
    P(X=1)=1−0,18−0,48P\left(X=1\right)=1-0,18-0,48
    Ainsi :
    P(X=1)=0,34P\left(X=1\right)=0,34
    Question 6

    Montrer que la variance de XX vaut 0,570,57.

    Correction
    On considère la loi de probabilité qui résument les questions précédentes.
      On appelle l’espérance mathématique de la variable XX, la quantité notée E(X)E\left(X\right) définie par :
    • E(X)=∑xi×pi=x1×p1+x2×p2+…+xn×pnE\left(X\right)=\sum x_{i} \times p_{i} =x_{1} \times p_{1}+x_{2} \times p_{2}+\ldots+ x_{n} \times p_{n}
     Calcul de l’espeˊrance :\red{\text{ Calcul de l'espérance :}}
    E(X)=0×0,18+1×0,34+2×0,48E\left(X\right)=0\times 0,18 +1\times 0,34+2\times 0,48
    Soit
    E(X)=1,3E\left(X\right)=1,3
    La formule de l'écart type σ\sigma est obtenue après avoir calculer la variance VV.
    Les formules de la variance et de l'écart type sont données ci-dessous :
    • V(X)=∑pi×(xi−E(X))2V\left(X\right)=\sum p_{i} \times \left(x_{i} -E\left(X\right)\right)^{2}
    • σ(X)=V(X)\sigma \left(X\right)=\sqrt{V\left(X\right)}
     Calcul de la variance :\red{\text{ Calcul de la variance :}}
    Il en résulte donc que :
    V(X)=∑(xi−E(X))2×piV\left(X\right)=\sum \left(x_{i} -E\left(X\right)\right) ^{2} \times p_{i}
    V(X)=(0−1,3)2×0,18+(1−1,3)2×0,34+(2−1,3)2×0,48V\left(X\right)=\left(0-1,3\right)^{2} \times 0,18+\left(1-1,3\right)^{2} \times 0,34+\left(2-1,3\right)^{2} \times 0,48
    Ainsi :
    V(X)=0,57V\left(X\right)=0,57

    Question 7

    A-t-on V(X)=V(X1)+V(X2)V\left(X\right)=V\left(X_1\right)+V\left(X_2\right) ? Est-ce surprenant ?

    Correction
    D'après la question 33 nous savons que P(B)=0,5P\left(B\right)=0,5 . Or PA(B)=0,6P_A\left(B\right)=0,6.
    Cela signifie que les évènements AA et BB ne sont pas indépendants car P(B)≠PA(B)P\left(B\right)\ne P_A\left(B\right)
    Les variables aléatoires X1X_1 et X2X_2 ne sont pas indépendantes ainsi V(X1+X1)≠V(X1)+V(X2)V\left(X_1+X_1\right)\ne V\left(X_1\right)+V\left(X_2\right)
      Soient XX et YY deux variables aléatoires indeˊpendantes\red{\text{indépendantes}}, on a :
  • V(X+Y)=V(X)+V(Y)V\left(X+Y\right)=V\left(X\right)+V\left(Y\right)