Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Repères et coordonnées - Exercice 2
15 min
25
On considère un cube .
L'espace est rapporté au repère orthonormé .
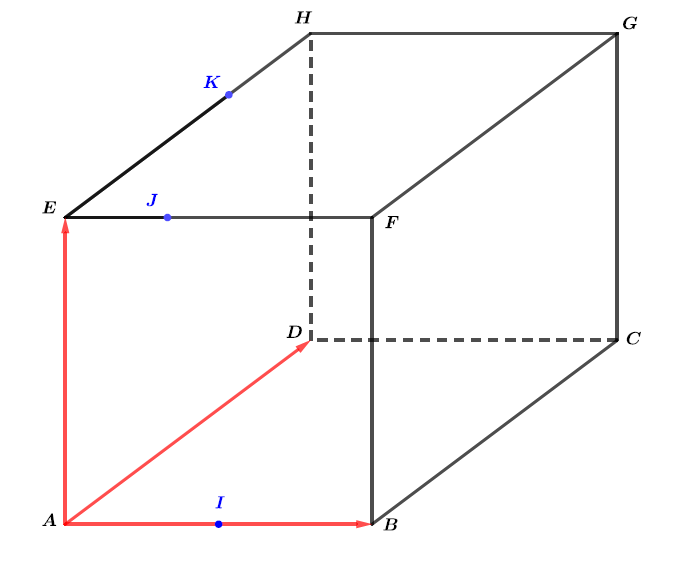
L'espace est rapporté au repère orthonormé .

- Le point est le milieu de
- Le point vérifie la relation
- Le point vérifie la relation
Question 1
Déterminer les coordonnées des points , , , et .
Correction
On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont
est l'origine du repère ainsi donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont
donc les coordonnées de sont car
donc les coordonnées de sont car
Question 2
Déterminer les coordonnées des points et .
Correction
est le milieu de ainsi les coordonnées de sont
On va maintenant donner les coordonnées de et .
D'après les hypothèses nous savons que : . D'après la relation de Chasles, on a :
Il est évident que : . Ainsi :
donc les coordonnées de sont
On va maintenant donner les coordonnées de et .
On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont
L'objectif est d'écrire par exemple que D'après les hypothèses nous savons que : . D'après la relation de Chasles, on a :
Il est évident que : . Ainsi :
donc les coordonnées de sont
Question 3
Déterminer les coordonnées du point .
Correction
On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont
D'après les hypothèses nous savons que : . D'après la relation de Chasles, on a : équivaut successivement à :
. Comme
donc les coordonnées de sont
Question 4
Montrer que les droites et sont parallèles.
Correction
On souhaite montrer si les droites et sont parallèles.
On connaît les coordonnées de et .
Si les vecteurs et colinéaires alors les et seront bien parallèles
On sait les coordonnées des points suivants ; ; et
On calcule les vecteurs et
Existe-t-il un réel tel que ?
On obtient le système suivant
Ainsi
Il en résulte que .
Les vecteurs et sont alors les droites et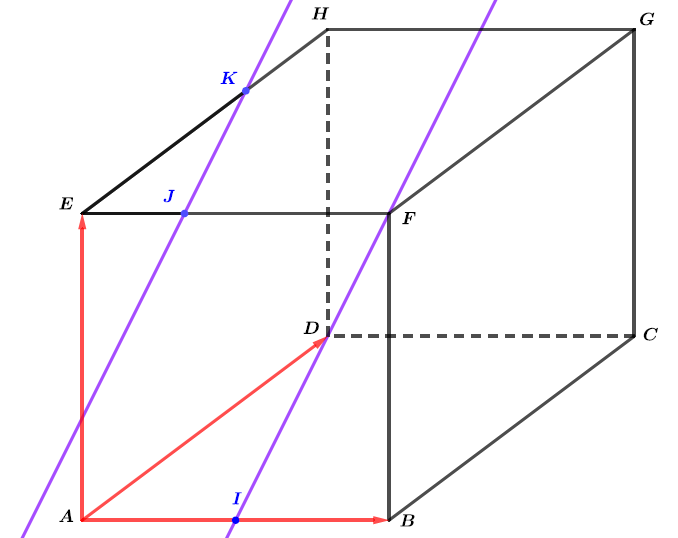
On connaît les coordonnées de et .
Si les vecteurs et colinéaires alors les et seront bien parallèles
On sait les coordonnées des points suivants ; ; et
On calcule les vecteurs et
Existe-t-il un réel tel que ?
On obtient le système suivant
Ainsi
Il en résulte que .
Les vecteurs et sont alors les droites et

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.