Nouveau

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Positions relatives : droites et plans - Exercice 1

2 min
5
On considère le cube ABCDEFGHABCDEFGH. MM et NN sont les milieux respectifs des segments [FE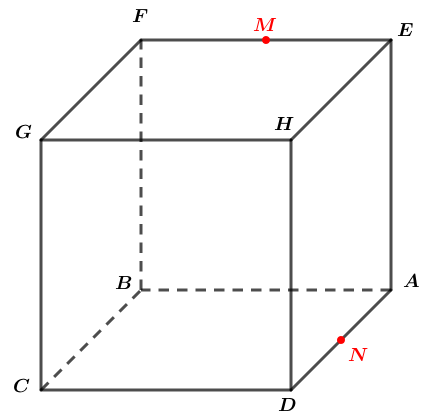]\left[FE\right] et [DA]\left[DA\right]
Dire pour chacune si les droites sont sécantes, parallèles ou non coplanaires.
Question 1

(HD)\left(HD\right) et (BF)\left(BF\right)

Correction
Les droites (HD)\left(HD\right) et (BF)\left(BF\right) sont paralleˋles\red{\text{parallèles}}.
  • Deux droites sont coplanaires si elles soient parallèles ou soient sécantes.
    • Question 2

    (GH)\left(GH\right) et (EA)\left(EA\right)

    Correction
    Les droites (GH)\left(GH\right) et (EA)\left(EA\right) sont non coplanaires.\red{\text{non coplanaires.}}
    Question 3

    (DN)\left(DN\right) et (BA)\left(BA\right)

    Correction
    Les droites (DN)\left(DN\right) et (BA)\left(BA\right) sont seˊcantes.\red{\text{sécantes.}}
  • Deux droites sont coplanaires si elles soient parallèles ou soient sécantes.
    • Question 4

    (NE)\left(NE\right) et (MH)\left(MH\right)

    Correction
    Les droites (NE)\left(NE\right) et (MH)\left(MH\right) sont non coplanaires.\red{\text{non coplanaires.}}

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.