Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Découvrir les vecteurs dans l'espace - Exercice 1
10 min
20
On considère le pavé droit .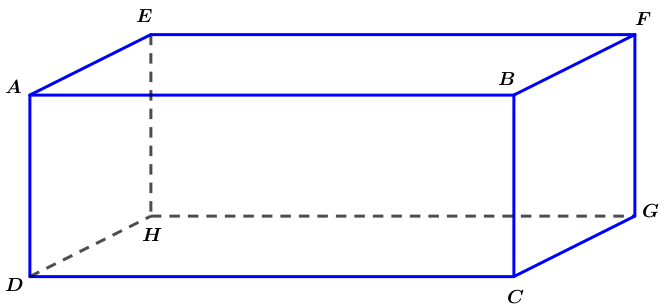

Question 1
Donner deux vecteurs égaux à
Correction
et sont égaux à .
Question 2
Comment peut-on simplifier le vecteur :
Correction

Nous savons que et que
Il vient alors que :
Maintenant nous pouvons calculer la relation de Chasles. Ainsi :
Ainsi :
Question 3
Donner trois vecteurs coplanaires.
Correction
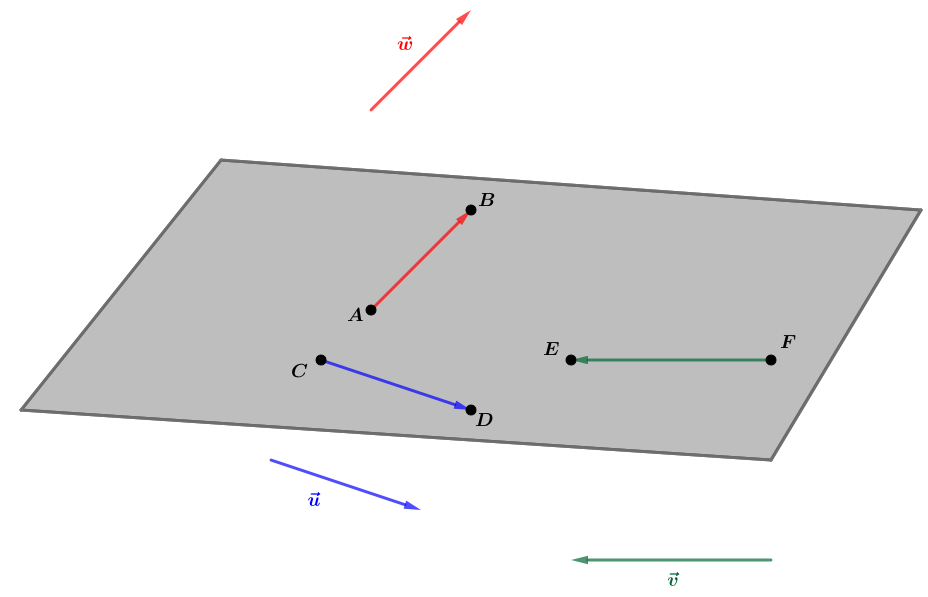
De plus, un représentant du vecteur sur le plan est le vecteur .
On vient de montrer que les vecteurs et et un représentant du vecteur appartiennent au plan .
Il en résulte donc que les vecteurs ; et sont coplanaires.

Question 4
Donner deux plans parallèles; deux plans sécants et deux plans confondus.
Correction

Question 5
Donner deux droites parallèles, deux droites orthogonales et deux droites sécantes. Parmi vos réponses quelles sont les droites également coplanaires.
Correction

Deux droites sont coplanaires (elles appartiennent à un même plan) si elles sont soient strictement parallèles ou confondues ou sécantes.
D'après le rappel :Question 6
Dans le repère . Déterminer les coordonnées du point .
Correction

On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont
Dans le repère est l'origine du repère ainsi
Question 7
Dans le repère . Déterminer les coordonnées du vecteur .
Correction
On considère le repère . Si l'on veut déterminer les coordonnées par exemple d'un point il faut l'exprimer le point avec l'origine du repère en fonction des vecteurs du repère donné. Dans notre exemple, si alors les coordonnées de sont
Nous connaissons les coordonnées du point , d'après la question .Nous allons déterminer maintenant les coordonnées du point .
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.