Fonctions trigonométriques
Sujet vue en Nouvelle-Calédonie novembre 2005 - Exercice 1
40 min
65
Un lapin désire traverser une route de mètres de largeur. Un camion, occupant toute la route, arrive à sa rencontre à la vitesse de km/h.
Le lapin décide au dernier moment de traverser, alors que le camion n’est plus qu’à mètres de lui.
Son démarrage est foudroyant et on suppose qu’il effectue la traversée en ligne droite au maximum de ses possibilités, c’est à dire à ... km/h!
L’avant du camion est représenté par le segment sur le schéma ci-dessous.
Le lapin part du point en direction de .
Cette direction est repérée par l’angle avec .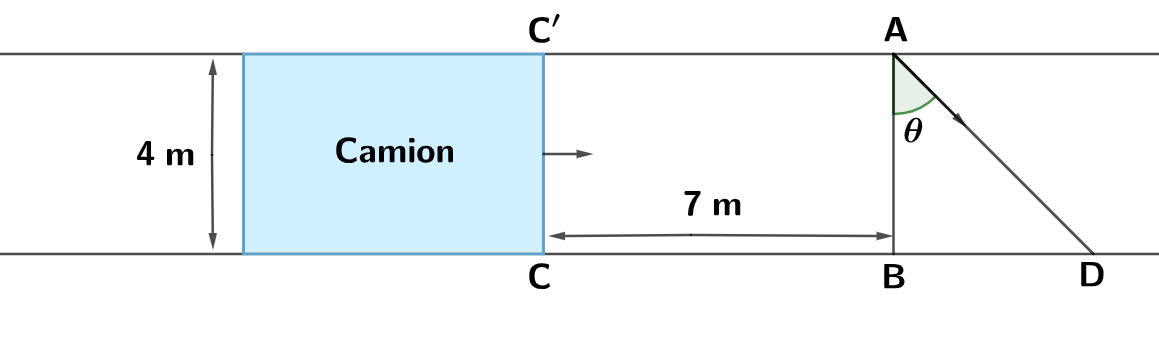
Le lapin décide au dernier moment de traverser, alors que le camion n’est plus qu’à mètres de lui.
Son démarrage est foudroyant et on suppose qu’il effectue la traversée en ligne droite au maximum de ses possibilités, c’est à dire à ... km/h!
L’avant du camion est représenté par le segment sur le schéma ci-dessous.
Le lapin part du point en direction de .
Cette direction est repérée par l’angle avec .

Question 1
Déterminer les distances et en fonction de et les temps et mis par le lapin et le camion pour parcourir respectivement les distances et .
Correction
Soit le triangle rectangle rectangle en .
On a alors :
D'une part :
Comme alors alors ainsi
D'autre part :
Or ce qui nous permet d'écrire :
Ainsi :
Nous pouvons finalement calculer .
En effet :
Finalement :
Nous allons maintenant calculer les temps et mis par le lapin et le camion pour parcourir respectivement les distances et .
On rappelle que
Calculons .
Ainsi
Nous allons exprimer la distance en kilomètre car la vitesse est exprimé en km/h. La vitesse sur la distance est de km/h .
Ainsi :Calculons . Ainsi
Nous allons exprimer la distance en kilomètre car la vitesse est exprimé en km/h. La vitesse sur la distance est de km/h .
On a alors :
D'une part :
Comme alors alors ainsi
car
D'autre part :
Or ce qui nous permet d'écrire :
Ainsi :
Nous pouvons finalement calculer .
En effet :
Finalement :
Nous allons maintenant calculer les temps et mis par le lapin et le camion pour parcourir respectivement les distances et .
On rappelle que
Ainsi
Nous allons exprimer la distance en kilomètre car la vitesse est exprimé en km/h. La vitesse sur la distance est de km/h .
Ainsi :
Nous allons exprimer la distance en kilomètre car la vitesse est exprimé en km/h. La vitesse sur la distance est de km/h .
Question 2
On pose .
Montrer que le lapin aura traversé la route avant le passage du camion si et seulement si .
Montrer que le lapin aura traversé la route avant le passage du camion si et seulement si .
Correction
Le lapin pourra traverser sans être écraser par le camion si .
Il vient alors que :
équivaut successivement à
. Nous allons multiplier ensuite tous les termes par .
. Nous allons diviser ensuite tous les termes par .
Ainsi :
Il vient alors que :
équivaut successivement à
. Nous allons multiplier ensuite tous les termes par .
. Nous allons diviser ensuite tous les termes par .
Ainsi :
Question 3
On considère la fonction définie sur l’intervalle par .
On admet que la fonction est dérivable sur l’intervalle et on note sa fonction dérivée.
Montrer que pour tout nombre réel de l’intervalle on a :
On admet que la fonction est dérivable sur l’intervalle et on note sa fonction dérivée.
Montrer que pour tout nombre réel de l’intervalle on a :
Correction
Ainsi : et .
Il vient alors que :
Pour tout réel , on a :
Autrement dit :
Question 4
On considère la fonction définie sur l’intervalle par .
On admet que la fonction est dérivable sur l’intervalle et on note sa fonction dérivée.
Montrer que pour tout nombre réel de l’intervalle on a :
On admet que la fonction est dérivable sur l’intervalle et on note sa fonction dérivée.
Montrer que pour tout nombre réel de l’intervalle on a :
Correction
Ainsi : .
Il vient alors que :
Ainsi :
Question 5
On considère la fonction définie sur l’intervalle par .
On admet que la fonction est dérivable sur l’intervalle et on note sa fonction dérivée.
Etudier la fonction sur l'intervalle .
On admet que la fonction est dérivable sur l’intervalle et on note sa fonction dérivée.
Etudier la fonction sur l'intervalle .
Correction
Nous avons :
D'après les questions et nous pouvons écrire que :
Ainsi :
Pour tout nombre réel de l’intervalle on peut affirmer que
Il en résulte que le signe de dépend du numérateur .
résoudre l'équation sur l'intervalle
Or , ainsi
L'unique solution sur de l'équation est
on résout puis on va utiliser le cercle trigonométrique.
Le segment vert représente la zone où . Ainsi entre on aura , c'est-à-dire .
On intègre cela dans un tableau ci-dessous. Il vient alors :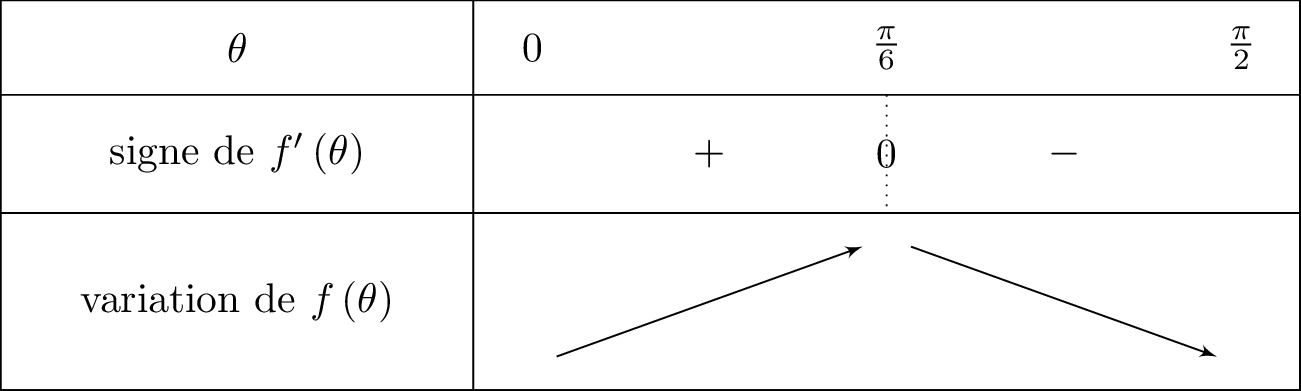
D'après les questions et nous pouvons écrire que :
Ainsi :
Pour tout nombre réel de l’intervalle on peut affirmer que
Il en résulte que le signe de dépend du numérateur .
résoudre l'équation sur l'intervalle
Or , ainsi
L'unique solution sur de l'équation est
on résout puis on va utiliser le cercle trigonométrique.
Le segment vert représente la zone où . Ainsi entre on aura , c'est-à-dire .
On intègre cela dans un tableau ci-dessous. Il vient alors :
