Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 4
25 min
45
Soit la fonction définie sur l'intervalle par : .
Question 1
Calculer et .
Correction
ainsi :
ainsi :
ainsi :
Question 2
Etudier et dresser son tableau de variation.
Correction
est dérivable sur .
Ici on reconnaît la forme avec et et
Ainsi : et , enfin
Il vient alors que :
Pour tout réel appartenant à l'intervalle , on sait que donc .
Pour tout réel appartenant à l'intervalle , on sait que .
Nous allons traduire cela dans un tableau de variation :

Ici on reconnaît la forme avec et et
Ainsi : et , enfin
Il vient alors que :
Pour tout réel appartenant à l'intervalle , on sait que donc .
Pour tout réel appartenant à l'intervalle , on sait que .
Nous allons traduire cela dans un tableau de variation :

Question 3
Soit la fonction définie sur l'intervalle par : .
Calculer puis et enfin .
Correction
est dérivable sur . Ainsi :
est dérivable sur . Ainsi :
est dérivable sur . Ainsi :
est dérivable sur . Ainsi :
est dérivable sur . Ainsi :
Question 4
Dresser le tableau de variation de sur .
Correction
Pour tout réel appartenant à , on a :
Or :
équivaut successivement à :
. Ainsi sur l'intervalle , on a : .
De plus :
c'est à dire
c'est à dire
Nous traduisons cela dans un tableau de variation :

Or :
équivaut successivement à :
. Ainsi sur l'intervalle , on a : .
De plus :
c'est à dire
c'est à dire
Nous traduisons cela dans un tableau de variation :

Question 5
En déduire les variations de sur .
Correction
D'après la question , on vérifie facilement que . En effet, est strictement croissante et son minimum vaut .
Il en résulte donc que est croissante sur l'intervalle .
De plus :
ainsi
ainsi et
Nous traduisons cela dans un tableau de variation :
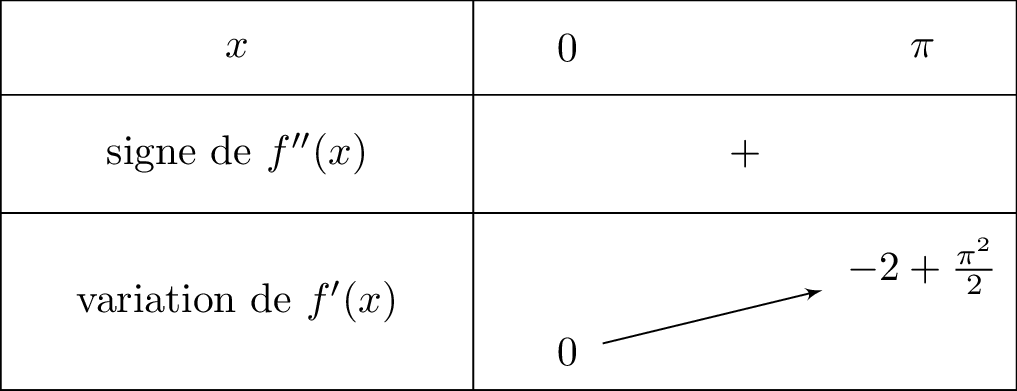
Il en résulte donc que est croissante sur l'intervalle .
De plus :
ainsi
ainsi et
Nous traduisons cela dans un tableau de variation :

Question 6
En déduire les variations de sur .
Correction
D'après la question , on vérifie facilement que . En effet, est strictement croissante et son minimum vaut .
Il en résulte donc que est croissante sur l'intervalle .
De plus :
ainsi
ainsi et
Nous traduisons cela dans un tableau de variation :
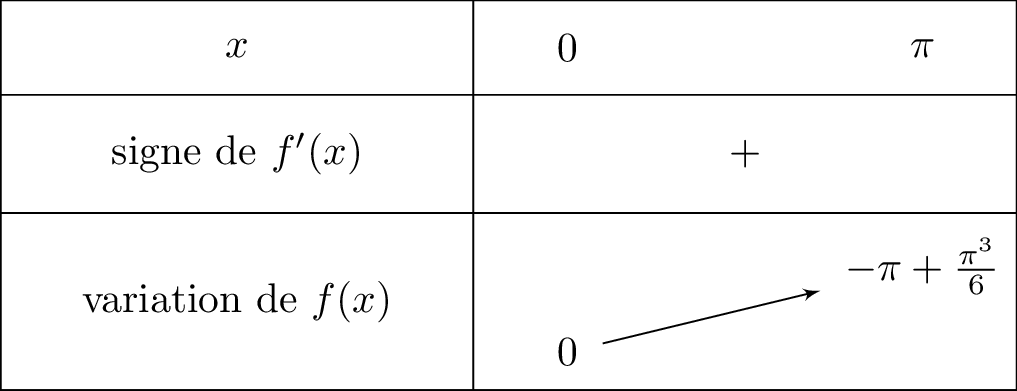
Il en résulte donc que est croissante sur l'intervalle .
De plus :
ainsi
ainsi et
Nous traduisons cela dans un tableau de variation :

Question 7
En déduire que pour tout réel appartenant à , on a :
Correction
D'après la question , on vérifie facilement que . En effet, est strictement croissante et son minimum vaut .
Il en résulte donc que sur l'intervalle , on a :
ce qui signifie que : .
De plus, pour tout réel appartenant à , on a : .
Autrement, pour tout réel appartenant à :
Il en résulte donc que sur l'intervalle , on a :
ce qui signifie que : .
De plus, pour tout réel appartenant à , on a : .
Autrement, pour tout réel appartenant à :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.