Qui aura 20 en maths ?

💯 Le grand concours 100% Terminale revient le 31 mai 2026 en ligne !Découvrir  →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Travailler avec des diagrammes - Exercice 1

6 min
10
Dans un lycée, on dénombre 100100 premières spécialités. On s'intéresse à ceux qui ont pris les options maths (MM), Physique (PP) et SVT (SS).
  • 3535 ont choisi l'option maths , 2020 ont choisi la physique et 5353 ont choisi la SVT.

    • De plus:
  • 88 ont choisi Maths et Physique
  • 99 ont choisi Physique et SVT
  • 1919 ont choisi maths et SVT et 55 ont choisi maths, physique et SVT.
    • Question 1

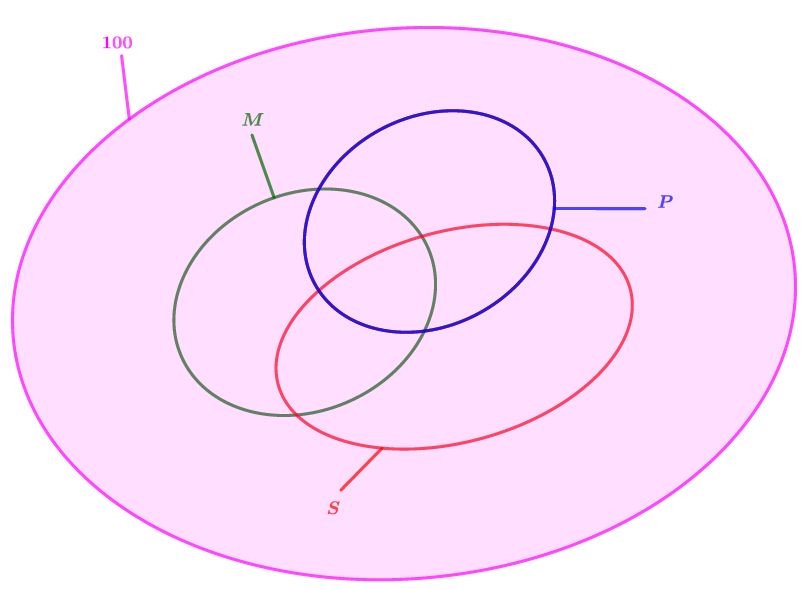
    Reproduire et compléter le diagramme ci-dessus :

    Correction
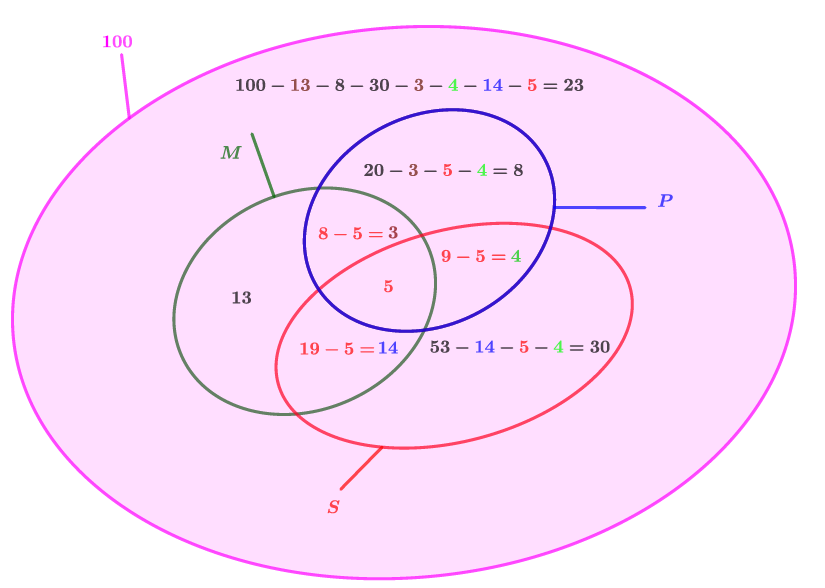
  • Pour la culture :) ce type de diagramme est appelé diagramme de Venn .\text{\red{diagramme de Venn .}}
    • Le nombre 2323 correspond à ceux qui ne font rien et il est important de le déterminer. Même ci cela fera l'objet d'une question, comme il s'agit du premier exercice de ce type que nous vous proposons, on souhaitait vous faire ce rappel.
    Question 2

    Déterminer les cardinaux de MM ; PP et SS

    Correction
    D'après l’énoncé, nous savons que :
    3535 ont choisi l'option maths , 2020 ont choisi la physique et 5353 ont choisi la SVT.
  • On appelle cardinal d'un ensemble EE et on note card(E)\text{card}\left(E\right), le nombre d'éléments de EE .
  • L’ensemble MM est composée de 3535 élèves donc
    card(M)=35\text{card}\left(M\right)=35
  • L’ensemble PP est composée de 2020 élèves donc
    card(P)=20\text{card}\left(P\right)=20
  • L’ensemble SS est composée de 5353 élèves donc
    card(S)=53\text{card}\left(S\right)=53
    • Question 3

    Déterminer le nombres de personnes qui ne font aucunes matières scientifiques.

    Correction
    D'après le diagramme complété à la question 11, il apparaît donc qu'il y a 2323 personnes qui n'étudient pas de matières scientifiques.
    Question 4

    Déterminer le nombre de personnes qui font des maths ou de la physique .

    Correction
  • card(A∪B)=card(A)+card(B)−card(A∩B)\text{card}\left(A\cup B\right)=\text{card}\left(A\right)+\text{card}\left(B\right)-\text{card}\left(A\cap B\right)
    • Nous souhaitons déterminer card(M∪P)\text{card}\left(M\cup P\right), d'après la formule, il vient que :
    card(M∪P)=card(M)+card(P)−card(M∩P)\text{card}\left(M\cup P\right)=\text{card}\left(M\right)+\text{card}\left(P\right)-\text{card}\left(M\cap P\right)
    card(M∪P)=35+20−8\text{card}\left(M\cup P\right)=35+20-8
    Ainsi :
    card(M∪P)=47\text{card}\left(M\cup P\right)=47

    Signaler une erreur

    Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

    Connecte-toi ou crée un compte pour signaler une erreur.