Qui aura 20 en maths ?

💯 Teste ton niveau de maths et tente de gagner un des lots !S'inscrire au jeu →

Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →

Exercices types : Des probas et des suites - Exercice 2

40 min

Dans un zoo, l'unique activité d'un manchot est l'utilisation d'un bassin aquatique équipé d'un toboggan et d'un plongeoir.
On a observé que :
Si un manchot choisit le toboggan, la probabilité qu'il le reprenne est

0,3

.
Si un manchot choisit le plongeoir, la probabilité qu'il le reprenne est

0,8

.
Lors du premier passage les deux équipements ont la même probabilité d'être choisis.

Pour tout entier naturel n non nul, on considère l'évènement :

$T_{n}$ : « le manchot utilise le toboggan lors de son $n$ -ième passage. »
$P_{n}$ : « le manchot utilise le plongeoir lors de son $n$ -ième passage. »

On considère alors la suite

\left(u_{n} \right)

définie pour tout entier naturel

n\ge 1

par :

u_{n} =p\left(T_{n} \right)

où

u_{n} =p\left(T_{n} \right)

est la probabilité de l'évènement

T_{n}

Question 1

Donner les valeurs des probabilités $p\left(T_{1} \right)$ , $p\left(P_{1} \right)$ et des probabilités conditionnelles $p_{T_{1} } \left(T_{2} \right)$ et $p_{P_{1} } \left(T_{2} \right)$ .

Correction

T_{1}

P_{1}

étant équiprobables alors

p\left(T_{1} \right)=p\left(P_{1} \right)=\frac{1}{2}

.
D'après l'énoncé la probabilité de prendre le toboggan après avoir pris le plongeoir est égale à

p_{P_{1} } \left(T_{2} \right)=1-0,8=0,2

.
Toujours d'après l'énoncé

p_{T_{1} } \left(T_{2} \right)=0,3

Question 2

Montrer que $p\left(T_{2} \right)=\frac{1}{4}$ .

Correction

Nous résumons l'ensemble des informations de la question dans un arbre pondéré :

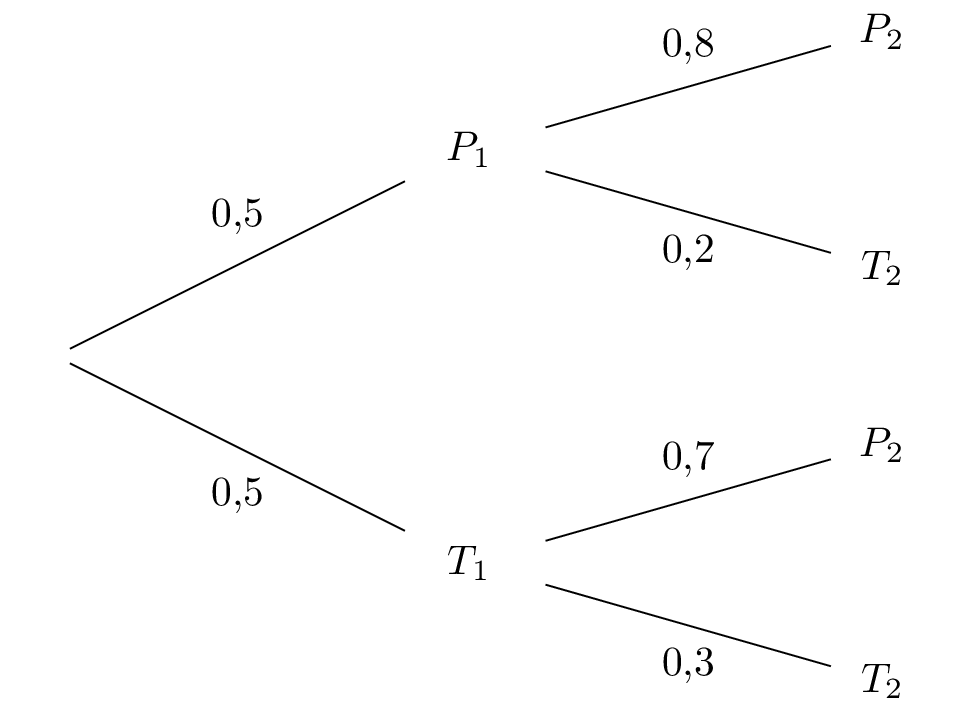Les évènements

T_{1}

P_{1}

forment une partition de l'univers.
D'après la formule des probabilités totales, on a :

p\left(T_{2} \right)=P\left(P_{1} \cap T_{2} \right)+P\left(T_{1} \cap T_{2} \right)

équivaut successivement à :

p\left(T_{2} \right)=P\left(P_{1} \right)\times p_{P_{1} } \left(T_{2} \right)+P\left(T_{1} \right)\times p_{P_{1} } \left(T_{2} \right)

p\left(T_{2} \right)=0,5\times 0,2+0,5\times 0,3

p\left(T_{2} \right)=0,10+0,15

p\left(T_{2} \right)=0,25

Ainsi :

p\left(T_{2} \right)=\frac{1}{4}

Question 3

Recopier et compléter l'arbre suivant :

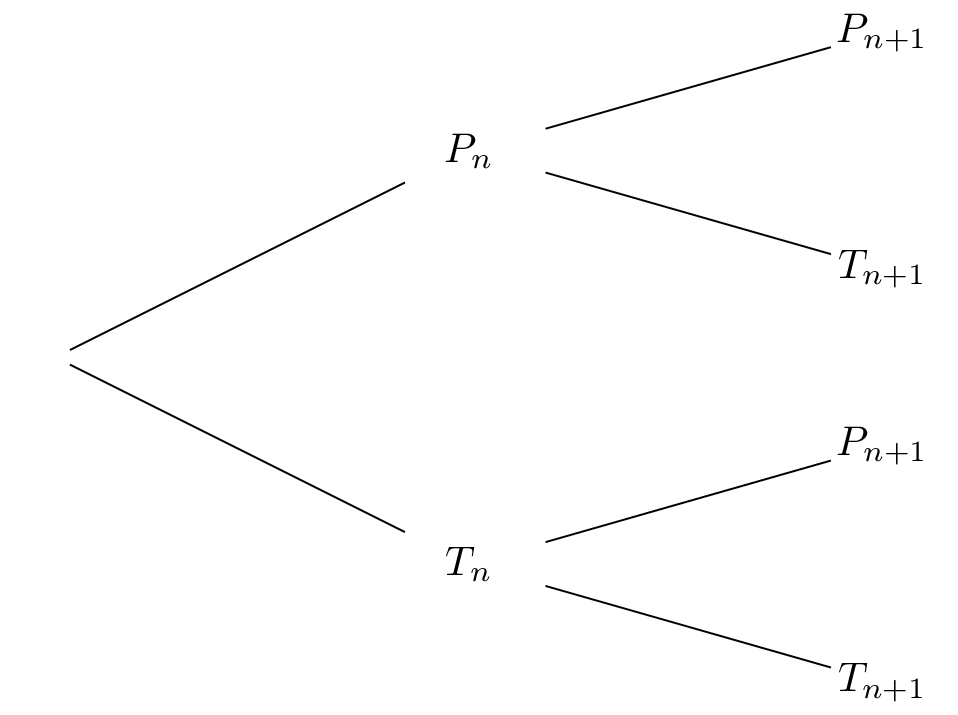
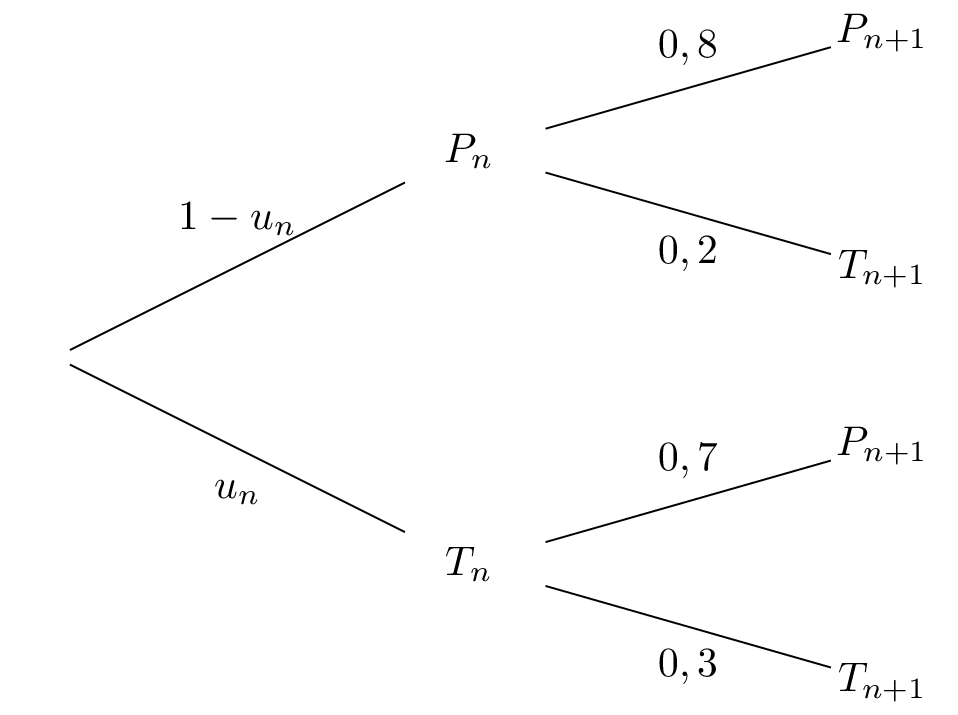
Correction

Avec les données de l'énoncé, il en résulte que :

Question 4

Démontrer que pour tout entier $n\ge 1$ , $u_{n+1} =0,1u_{n} +0,2$

Correction

Les évènements

T_{n}

P_{n}

forment une partition de l'univers.
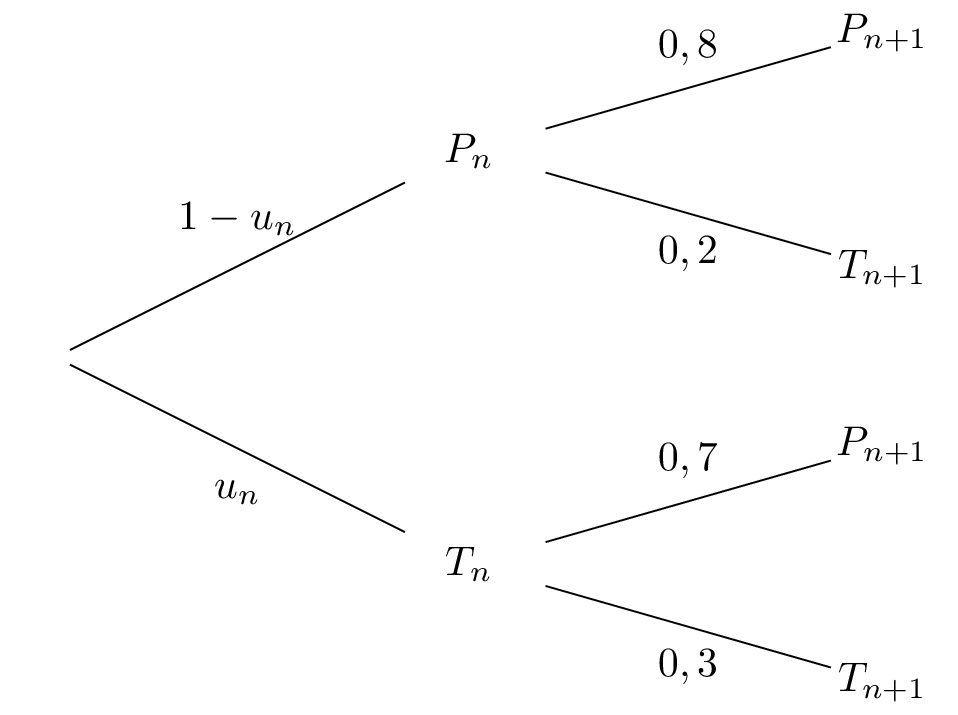
D'après la formule des probabilités totales, on a :

u_{n+1} =p\left(T_{n+1} \right)

équivaut successivement à :

u_{n+1} =P\left(P_{n} \cap T_{n+1} \right)+P\left(T_{n} \cap T_{n+1} \right)

u_{n+1} =P\left(P_{n} \right)\times p_{P_{n} } \left(T_{n+1} \right)+P\left(T_{n} \right)\times p_{T_{n} } \left(T_{n+1} \right)

u_{n+1} =\left(1-u_{n} \right)\times 0,2+u_{n} \times 0,3

u_{n+1} =0,2-0,2u_{n} +0,3u_{n}

Ainsi :

u_{n+1} =0,1u_{n} +0,2

Question 5

A l'aide de la calculatrice, émettre une conjecture concernant la limite de la suite $\left(u_{n} \right)$ .

Correction

En utilisant la calculatrice, on remarque que :

u_{1} =0,5

;

u_{2} =0,25

;

u_{3} =0,225

;

u_{4} =0,225

;

u_{5} =0,2225

.
On conjecture que

u_{n}

ait comme limite

0,222.......

Question 6

On considère la suite

\left(v_{n} \right)

définie pour tout entier naturel

n\ge 1

par :

v_{n} =u_{n} -\frac{2}{9}

Démontrer que la suite $\left(v_{n} \right)$ est géométrique de raison $\frac{1}{10}$ .
Préciser son premier terme.

Correction

On sait que :

v_{n} =u_{n} -\frac{2}{9}

Ainsi :

v_{n+1} =u_{n+1} -\frac{2}{9}

u_{n+1} =0,1u_{n} +0,2

D'où :

v_{n+1} =0,1u_{n} +0,2-\frac{2}{9}

v_{n+1} =0,1u_{n} +\frac{1}{5} -\frac{2}{9}

v_{n+1} =0,1{\color{blue}{u_{n}}} -\frac{1}{45}

v_{n} =u_{n} -\frac{2}{9}

donc

{\color{blue}{v_{n} +\frac{2}{9} =u_{n}}}

, on substitue dans la dernière expression , ce qui donne :

v_{n+1} =0,1\left({\color{blue}{v_{n} +\frac{2}{9} }} \right)-\frac{1}{45}

v_{n+1} =\frac{1}{10} \left(v_{n} +\frac{2}{9} \right)-\frac{1}{45}

v_{n+1} =\frac{1}{10} v_{n} +\frac{1}{45} -\frac{1}{45}

v_{n+1} =\frac{1}{10} v_{n}

Finalement :

\left(v_{n} \right)

est une suite géométrique de raison

\frac{1}{10}

.
Son premier terme est alors :

v_{1} =u_{1} -\frac{2}{9}

.
Ainsi :

v_{1} =\frac{1}{2} -\frac{2}{9} =\frac{5}{18}

Question 7

Exprimer $v_{n}$ en fonction de $n$ .
En déduire l'expression de $u_{n}$ en fonction de $n$ .

Correction

L'expression de $u_{n}$ en fonction de $n$ est donnée par la formule
$u_{n} =u_{1} \times q^{n-1}$

Il vient alors que :

v_{n} =\frac{5}{18} \times \left(\frac{1}{10} \right)^{n-1}

Comme

v_{n} =u_{n} -\frac{2}{9}

donc

v_{n} +\frac{2}{9} =u_{n}

Alors :

u_{n} =\frac{5}{18} \times \left(\frac{1}{10} \right)^{n-1} +\frac{2}{9}

Question 8

Calculer la limite de la suite $\left(u_{n} \right)$ .
Ce résultat permet-il de valider la conjecture émise à la question 5 ?

Correction

Si $-1<q<1$ alors $\lim\limits_{n\to +\infty } q^{n} =0$ .
Si $q >1$ alors $\lim\limits_{n\to +\infty } q^{n} =+\infty$ .

Comme

-1<\frac{1}{10} <1

\lim\limits_{n\to +\infty } \left(\frac{1}{10} \right)^{n-1} =0

Donc :

\lim\limits_{n\to +\infty } \frac{5}{18} \times \left(\frac{1}{10} \right)^{n-1} =0

Il en résulte que :

\lim\limits_{n\to +\infty } \frac{5}{18} \times \left(\frac{1}{10} \right)^{n-1} +\frac{2}{9} =\frac{2}{9}

Donc :

\lim\limits_{n\to +\infty } u_{n} =\frac{2}{9}

Cette valeur est

\frac{2}{9} =0.222...

ce qui valide la conjecture faite à la question

5

Exercices types : Des probas et des suites - Exercice 2

Donner les valeurs des probabilités p(T1)p\left(T_{1} \right)p(T1​), p(P1)p\left(P_{1} \right)p(P1​) et des probabilités conditionnelles pT1(T2)p_{T_{1} } \left(T_{2} \right)pT1​​(T2​) et pP1(T2)p_{P_{1} } \left(T_{2} \right)pP1​​(T2​).

Montrer que p(T2)=14p\left(T_{2} \right)=\frac{1}{4} p(T2​)=41​.

Recopier et compléter l'arbre suivant :

Démontrer que pour tout entier n≥1n\ge 1n≥1, un+1=0,1un+0,2u_{n+1} =0,1u_{n} +0,2un+1​=0,1un​+0,2

A l'aide de la calculatrice, émettre une conjecture concernant la limite de la suite (un)\left(u_{n} \right)(un​).

Démontrer que la suite (vn)\left(v_{n} \right)(vn​) est géométrique de raison 110\frac{1}{10} 101​ .Préciser son premier terme.

Exprimer vnv_{n} vn​ en fonction de nnn.En déduire l'expression de unu_{n} un​ en fonction de nnn.

Calculer la limite de la suite (un)\left(u_{n} \right)(un​).Ce résultat permet-il de valider la conjecture émise à la question 5 ?

Donner les valeurs des probabilités $p\left(T_{1} \right)$ , $p\left(P_{1} \right)$ et des probabilités conditionnelles $p_{T_{1} } \left(T_{2} \right)$ et $p_{P_{1} } \left(T_{2} \right)$ .

Montrer que $p\left(T_{2} \right)=\frac{1}{4}$ .

Démontrer que pour tout entier $n\ge 1$ , $u_{n+1} =0,1u_{n} +0,2$

A l'aide de la calculatrice, émettre une conjecture concernant la limite de la suite $\left(u_{n} \right)$ .

Démontrer que la suite $\left(v_{n} \right)$ est géométrique de raison $\frac{1}{10}$ .
Préciser son premier terme.

Exprimer $v_{n}$ en fonction de $n$ .
En déduire l'expression de $u_{n}$ en fonction de $n$ .

Calculer la limite de la suite $\left(u_{n} \right)$ .
Ce résultat permet-il de valider la conjecture émise à la question 5 ?