Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : Des probas et des suites - Exercice 1
30 min
45
Un jeu de hasard sur ordinateur est paramétré de la façon suivante :
Si le joueur gagne une partie, la probabilité qu’il gagne la partie suivante est Si le joueur perd une partie, la probabilité qu’il perde la partie suivante est La probabilité de gagner la première partie est
Question 1
Pour tout entier naturel non nul, on note l’évènement « la nième partie est gagnée » et on note la probabilité de cet évènement. On a donc
Montrer que .
Correction
Nous allons commencer par dresser l'arbre de probabilité traduisant la situation : 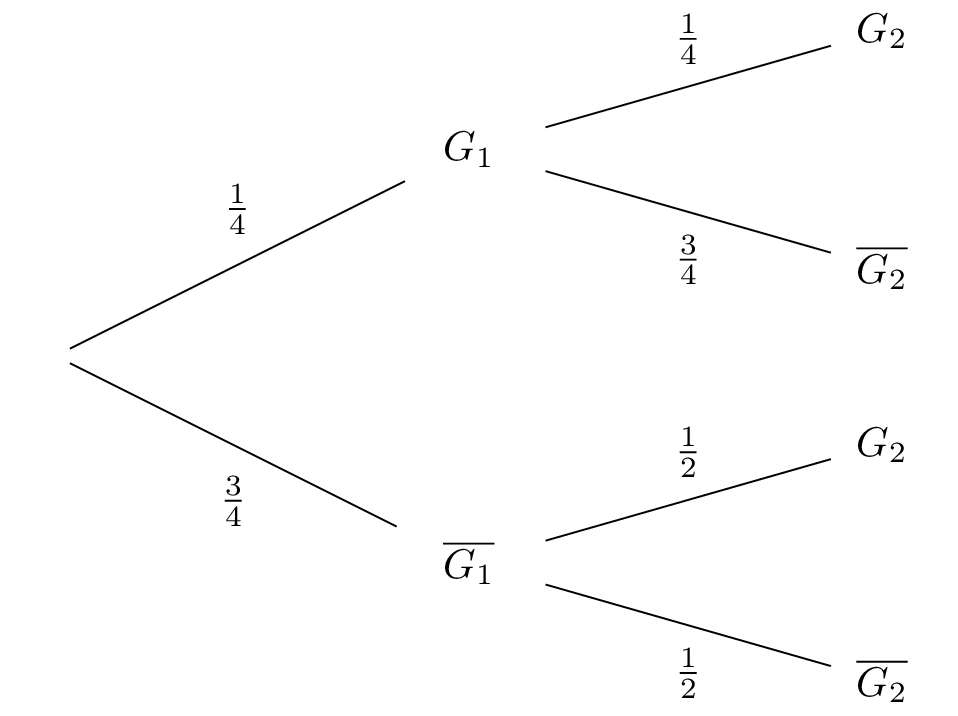 On note la probabilité de l'évènement , c'est à dire .
On note la probabilité de l'évènement , c'est à dire .
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales, on a :

Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales, on a :
Question 2
Montrer que, pour tout entier naturel non nul, .
Correction
Nous allons commencer par dresser l'arbre de probabilité traduisant la situation :
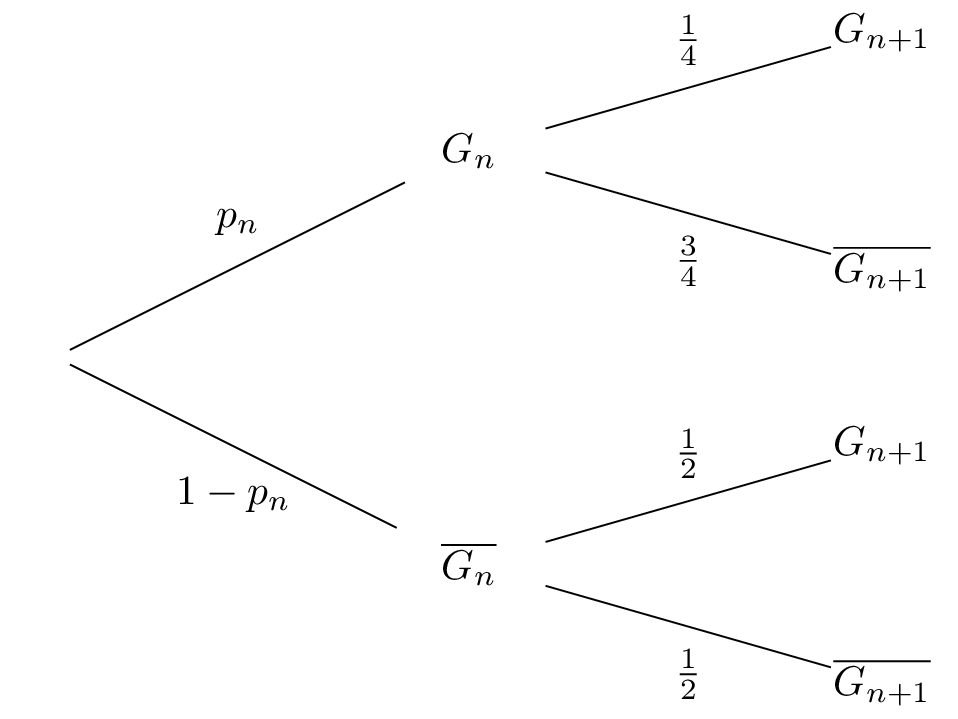 On note la probabilité de l'évènement .
On note la probabilité de l'évènement .
Il vient alors que la probabilité de l'évènement , c'est-à-dire : .
Les évènements et forment une partition de l'univers.
D'après la loi des probabilités totales, on a :

Il vient alors que la probabilité de l'évènement , c'est-à-dire : .
Les évènements et forment une partition de l'univers.
D'après la loi des probabilités totales, on a :
Question 3
On obtient ainsi les premières valeurs de : 

Quelle conjecture peut-on émettre?
Correction
On peut conjecturer que la suite converge vers .
Question 4
On définit, pour tout entier naturel non nul, la suite par .
Démontrer que la suite est une suite géométrique dont on précisera la raison.
Correction
Pour tout entier naturel non nul, on a :
Or : , il vient alors :
Or : d'où :
L'égalité montre que la suite est une suite géométrique de raison et de premier terme .
Or : , il vient alors :
Or : d'où :
L'égalité montre que la suite est une suite géométrique de raison et de premier terme .
Question 5
En déduire que, pour tout entier naturel non nul, .
Correction
- L'expression de en fonction de est donnée par la formule
Il nous reste plus qu'à donner l'expression de en fonction de .
Or : d'où :
Finalement :
Question 6
La suite converge-t-elle? Interpréter ce résultat.
Correction
- Si alors .
- Si alors .
Ainsi :
La conjecture faite à partir du tableau est validée.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.