Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
20 min
40
Une urne contient cinq boules indiscernables au toucher : deux vertes et trois rouges.
On extrait simultanément et au hasard deux boules de l’urne. On note la variable aléatoire égale au nombre de boules vertes figurant dans le tirage.
On extrait simultanément et au hasard deux boules de l’urne. On note la variable aléatoire égale au nombre de boules vertes figurant dans le tirage.
Question 1
Calculer
Correction
Les boules sont indiscernables au toucher, cela traduit donc la notion d'équiprobabilité.
De manière générale, pour tirer au hasard boules, il faut une combinaison de éléments dans un ensemble de .
Pour tirer boule verte, il nous faut donc tirer uniquement boules rouges. Il s'agit d'une combinaison de éléments dans un ensemble de .
Nous pouvons maintenant calculer
Ainsi :
Ainsi :
De manière générale, pour tirer au hasard boules, il faut une combinaison de éléments dans un ensemble de .
Pour tirer boule verte, il nous faut donc tirer uniquement boules rouges. Il s'agit d'une combinaison de éléments dans un ensemble de .
Nous pouvons maintenant calculer
Ainsi :
Ainsi :
Question 2
Déterminer la loi de probabilité de la variable aléatoire .
Correction
Pour déterminer la loi de probabilité de la variable aléatoire , il va nous falloir calculer dans un premier temps puis .
Il faut donc tirer boule verte parmi les boules vertes et boule rouge parmi les boules rouges. Ce qui nous donne :
Ainsi : Pour tirer boules vertes, il nous faut donc tirer uniquement les boules vertes et aucunes rouges. Il s'agit d'une combinaison de éléments dans un ensemble de . Ce qui nous donne :
Ainsi :
Nous pouvons maintenant donner la loi de probabilité de la variable aléatoire .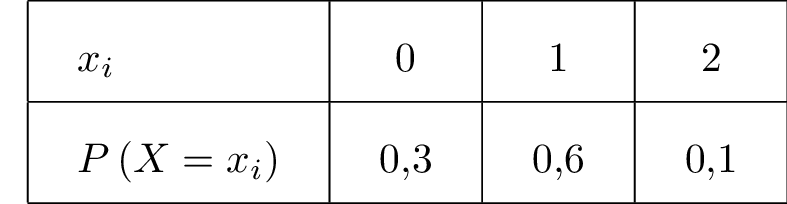
Ainsi :
Ainsi :
Nous pouvons maintenant donner la loi de probabilité de la variable aléatoire .

Question 3
Calculer l’espérance mathématique de la variable aléatoire .
Correction

On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Calculons l'espérance ( on peut également considérer que l'espérance est la moyenne )Soit :
Question 4
Calculer la probabilité de l’événement suivant : les deux boules tirées sont de même couleur
Correction
Il faut donc que les deux boules soient rouges ou alors que les deux boules soient vertes.
Il en résulte donc que :
Ainsi :
Il en résulte donc que :
Ainsi :
Question 5
On effectue deux tirages successifs d’une boule en respectant la règle suivante : si la boule tirée est rouge, on la remet dans l’urne; si elle est verte, on ne la remet pas.
Déterminer l'arbre pondéré traduisant la situation.
Correction
Notons les événements suivants pour déterminer l'arbre pondéré.
la boule tirée au premier tirage est verte et la boule tirée au premier tirage est rouge la boule tirée au deuxième tirage est verte et la boule tirée au deuxième tirage est rouge On a ainsi :
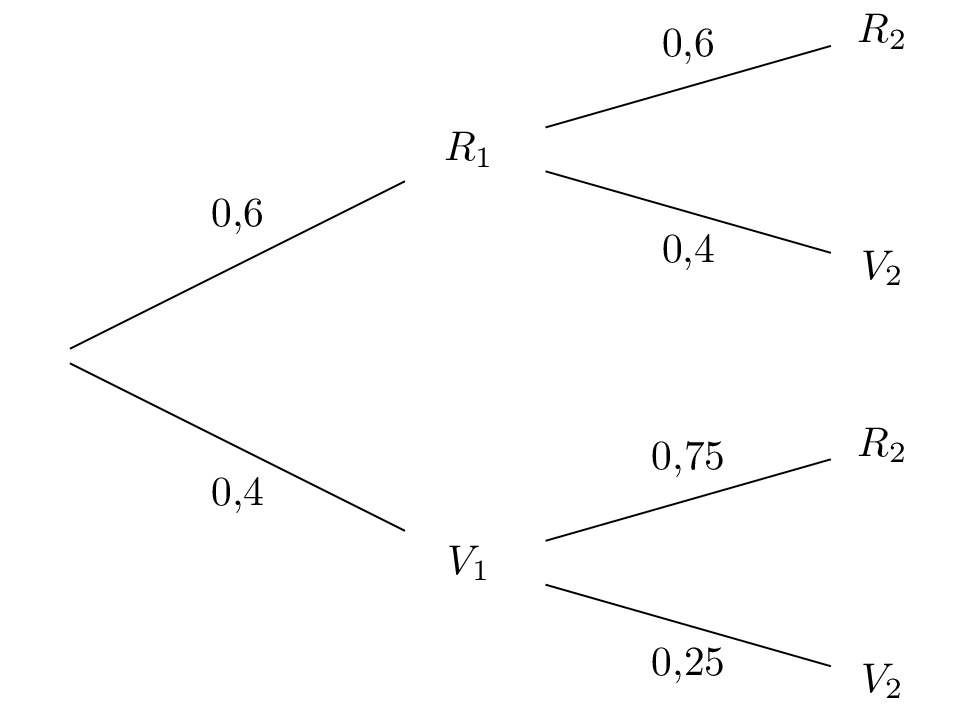

Question 6
Calculer la probabilité qu'une seule des deux boules tirées soit verte .
Correction
Notons une seule des deux boules tirées soit verte .
Il faut donc tirer soit une boule verte au premier tirage suivie d'une boule rouge ou alors tirer une boule rouge au premier tirage suivi d'une boule verte. Il vient alors que :
D'où :
Il faut donc tirer soit une boule verte au premier tirage suivie d'une boule rouge ou alors tirer une boule rouge au premier tirage suivi d'une boule verte. Il vient alors que :
D'où :
Question 7
Sachant que l’on a tiré exactement une boule verte, quelle est la probabilité que cette boule verte soit la première tirée ?
Correction
Il s'agit de calculer une probabilité conditionnelle.
. Dans notre situation, car il faut que nous tirions qu'une seule boule verte parmi les deux.
Finalement :
Finalement :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.