Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
15 min
30
Un sac contient jetons indiscernables au toucher : jetons blancs numérotés de à et jetons noirs numérotés de à .
On tire simultanément deux jetons de ce sac.
On tire simultanément deux jetons de ce sac.
Question 1
On note l’événement « obtenir deux jetons blancs ». Démontrer que la probabilité de l’événement est égale à .
Correction
Les jetons sont indiscernables au toucher, cela traduit donc la notion d'équiprobabilité.
De manière générale, pour tirer au hasard jetons, il faut une combinaison de éléments dans un ensemble de .
Pour tirer jetons blancs, il faut une combinaison de éléments dans un ensemble de .
Nous pouvons maintenant calculer
Ainsi :
Ainsi :
De manière générale, pour tirer au hasard jetons, il faut une combinaison de éléments dans un ensemble de .
Pour tirer jetons blancs, il faut une combinaison de éléments dans un ensemble de .
Nous pouvons maintenant calculer
Ainsi :
Ainsi :
Question 2
On note l’événement « obtenir deux jetons portant des numéros impairs ».
Calculer la probabilité de .
Calculer la probabilité de .
Correction
Les jetons sont indiscernables au toucher, cela traduit donc la notion d'équiprobabilité.
De manière générale, pour tirer au hasard jetons, il faut une combinaison de éléments dans un ensemble de .
Pour tirer jetons portant des numéros impairs, il faut une combinaison de éléments dans un ensemble de . Nous avons effectivement jetons portant des numéros impairs.
Nous pouvons maintenant calculer
Ainsi :
Ainsi :
De manière générale, pour tirer au hasard jetons, il faut une combinaison de éléments dans un ensemble de .
Pour tirer jetons portant des numéros impairs, il faut une combinaison de éléments dans un ensemble de . Nous avons effectivement jetons portant des numéros impairs.
Nous pouvons maintenant calculer
Ainsi :
Ainsi :
Question 3
Les événements et sont-ils indépendants ?
Correction
- Deux événements et sont indépendants si et seulement si :
-
Ainsi :
Or :
Ainsi :
les événements et
Question 4
Soit la variable aléatoire prenant pour valeur le nombre de jetons blancs obtenus lors de ce tirage simultané.
Déterminer la loi de probabilité de .
Correction
La variable aléatoire prend les valeurs ; ou .
: il faut donc tirer jeton blanc parmi les jetons blancs jetons noirs parmi les jetons noirs. Ce qui nous donne :
: il faut donc tirer jeton blanc parmi les jetons blancs jeton noir parmi les jetons noirs. Ce qui nous donne :
: il faut donc tirer jetons blancs parmi les jetons blancs jeton noir parmi les jetons noirs. Ce qui nous donne :
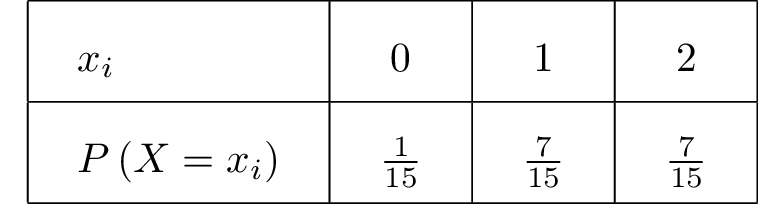
Nous dressons ci-dessous la loi de probabilité de :
: il faut donc tirer jeton blanc parmi les jetons blancs jetons noirs parmi les jetons noirs. Ce qui nous donne :
: il faut donc tirer jeton blanc parmi les jetons blancs jeton noir parmi les jetons noirs. Ce qui nous donne :
: il faut donc tirer jetons blancs parmi les jetons blancs jeton noir parmi les jetons noirs. Ce qui nous donne :
Nous dressons ci-dessous la loi de probabilité de :

Question 5
Calculer l’espérance mathématique de .
Correction
On appelle l’espérance mathématique de la variable , la quantité notée définie par :

D'où :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.