Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 4
25 min
40
Question 1
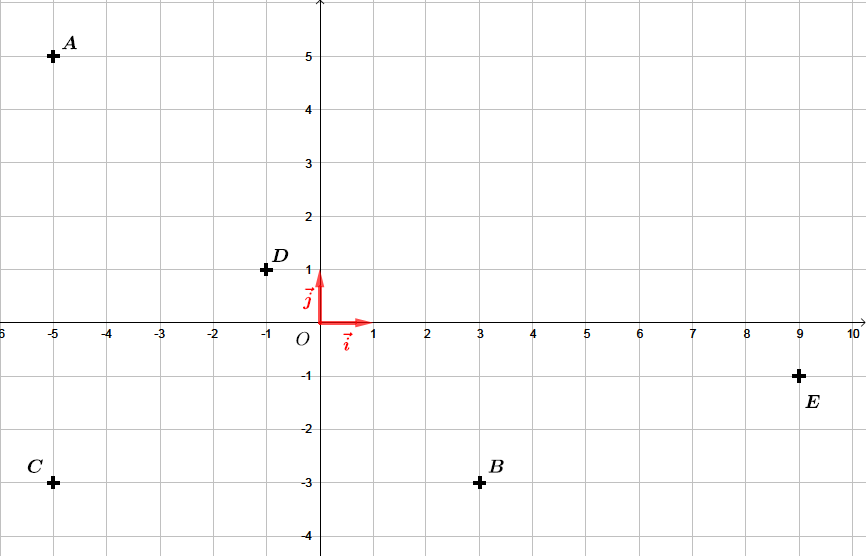
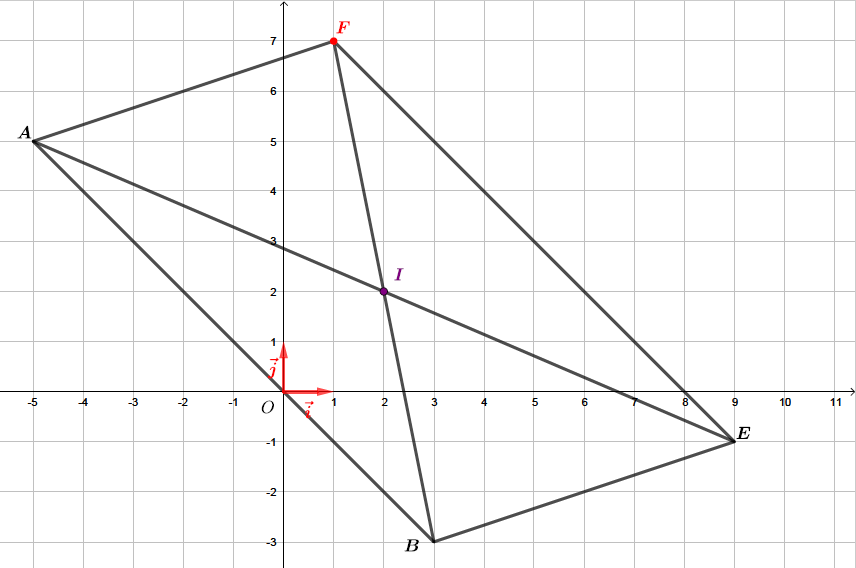
Soit un repère du plan. On considère les points : ; ; ; et
Placer les points dans un repère orthonormé.
Correction
Question 2
Montrer que le point est le milieu du segment .
Correction
Notons le milieu du segment .
équivaut successivement à :
Les coordonnées du milieu du segment sont .
Or les coordonnées du point sont les mêmes que celles du point .
Il en résulte donc que le point est bien le milieu du segment .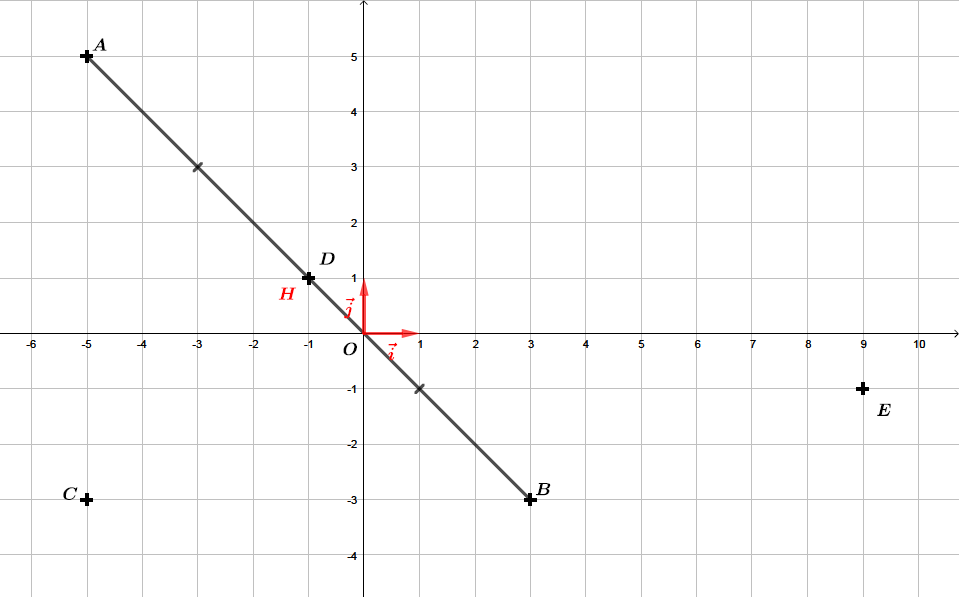
Soit un repère du plan et deux points et
Il vient alors que :- Les coordonnées du milieu du segment sont : et
équivaut successivement à :
Les coordonnées du milieu du segment sont .
Or les coordonnées du point sont les mêmes que celles du point .
Il en résulte donc que le point est bien le milieu du segment .

Question 3
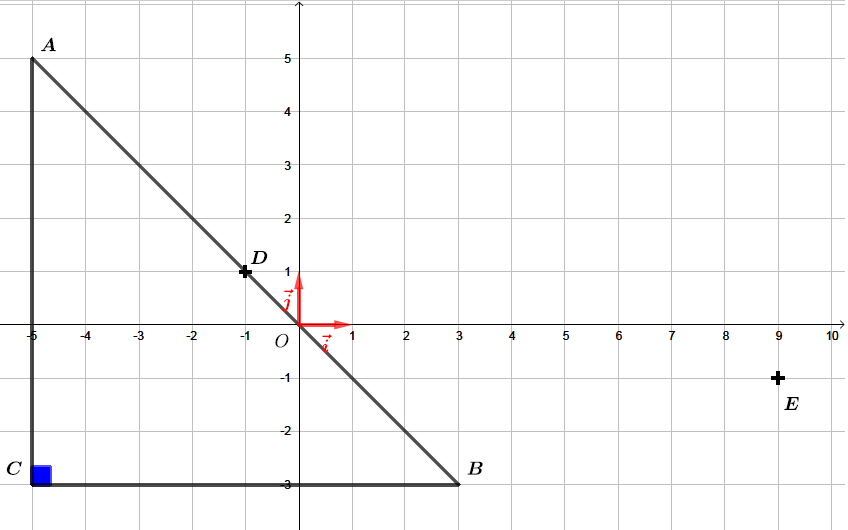
Montrer que le triangle est rectangle et isocèle en .
Correction
Il va nous falloir calculer les longueurs , et du triangle .
D'où :
D'où :
D'où :
Nous avons alors, d’après la réciproque du théorème de Pythagore, le triangle est rectangle en .
Soit un repère orthonormal du plan et deux points et . La distance est donnée par la formule :
Ainsi :D'où :
D'où :
D'où :
Nous avons alors, d’après la réciproque du théorème de Pythagore, le triangle est rectangle en .

Question 4
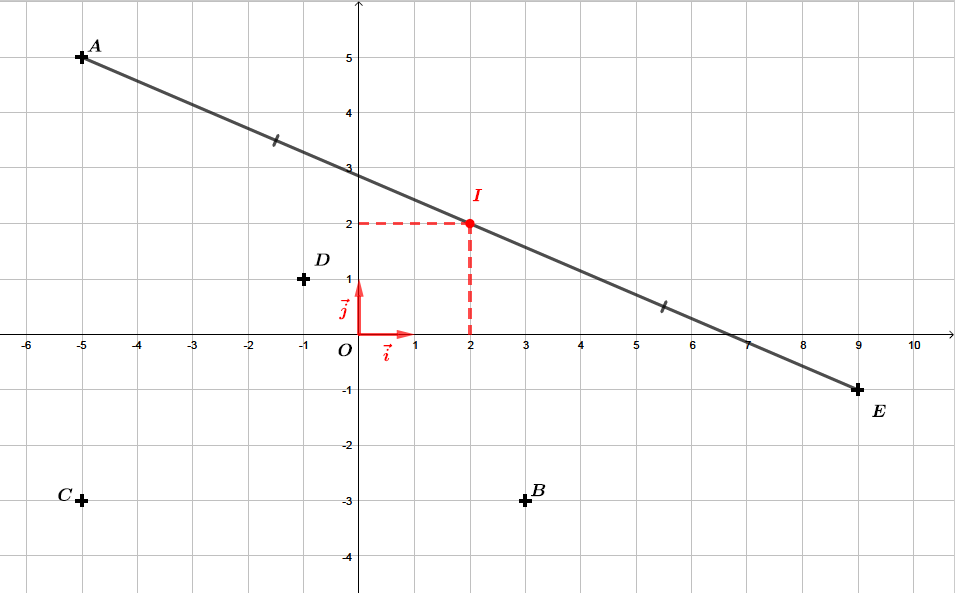
Déterminer les coordonnées du point milieu de .
Correction
Soit un repère du plan et deux points et
Il vient alors que :- Les coordonnées du milieu du segment sont : et
équivaut successivement à :
Les coordonnées du milieu du segment sont .
Question 5
A l'aide du point déterminer les coordonnées du point tel que soit un parallélogramme.
Correction
- Si un quadrilatère a ses diagonales qui se coupent en leur milieu, alors c'est un parallélogramme .
D'après la question nous savons que le point est le milieu du segment . Pour que soit un parallélogramme, il faut que le point soit également le milieu du segment .
Soit le point recherché. Il vient alors que :
équivaut successivement à :
. Ici, nous allons tout mettre au même dénominateur.
équivaut successivement à :
. Ici, nous allons tout mettre au même dénominateur.
Les coordonnées du point tel que soit un parallélogramme sont
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.