Nouveau
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ème partie - Exercice 2
25 min
45
Question 1
Considérons un parallélogramme .
Soit l'image du point par la translation de vecteur
Considérons le point tel que le point soit le milieu de et le point tel que le point soit le milieu de
Soit l'image du point par la translation de vecteur
Considérons le point tel que le point soit le milieu de et le point tel que le point soit le milieu de
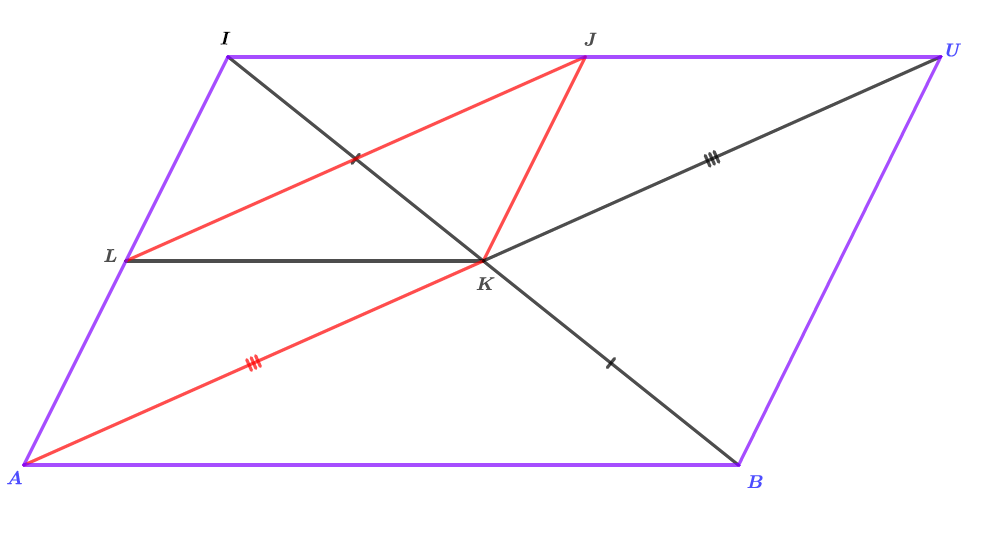
Faire une figure.
Correction
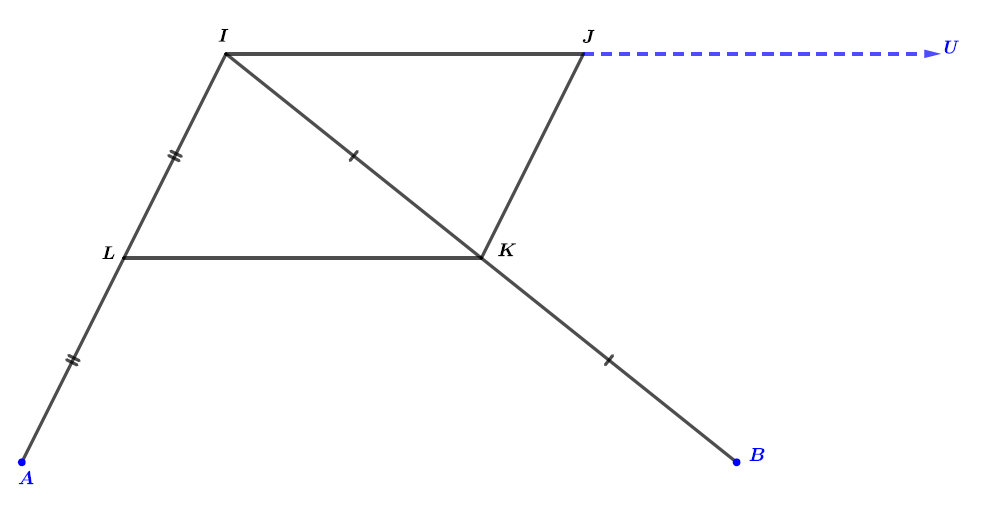
Question 2
Montrer que .
Correction
Nous savons que est un parallèlogramme ce qui nous permet d'écrire .
Nous savons également que le point est l'image du point par la translation de vecteur . Cela signifie que
Il en résulte donc que . Cette égalité permet de démontrer que le quadrilatère est un parallèlogramme.
Le fait que le quadrilatère est un parallèlogramme alors nous pouvons conclure que :
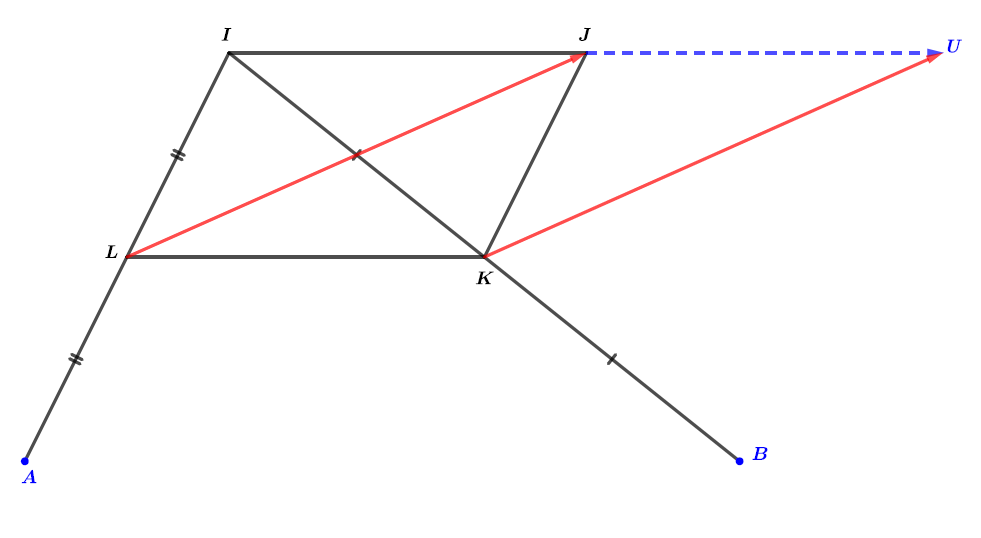
Nous savons également que le point est l'image du point par la translation de vecteur . Cela signifie que
Il en résulte donc que . Cette égalité permet de démontrer que le quadrilatère est un parallèlogramme.
Le fait que le quadrilatère est un parallèlogramme alors nous pouvons conclure que :

Question 3
Quel est la nature du quadrilatère . Justifier.
Correction
Le point soit le milieu de cela signifie que .
Nous savons également que est un parallélogramme ce qui nous permet d'écrire .
Il en résulte donc que : . Cette égalité vectorielle permet de démontrer que le quadrilatère est un parallélogramme .
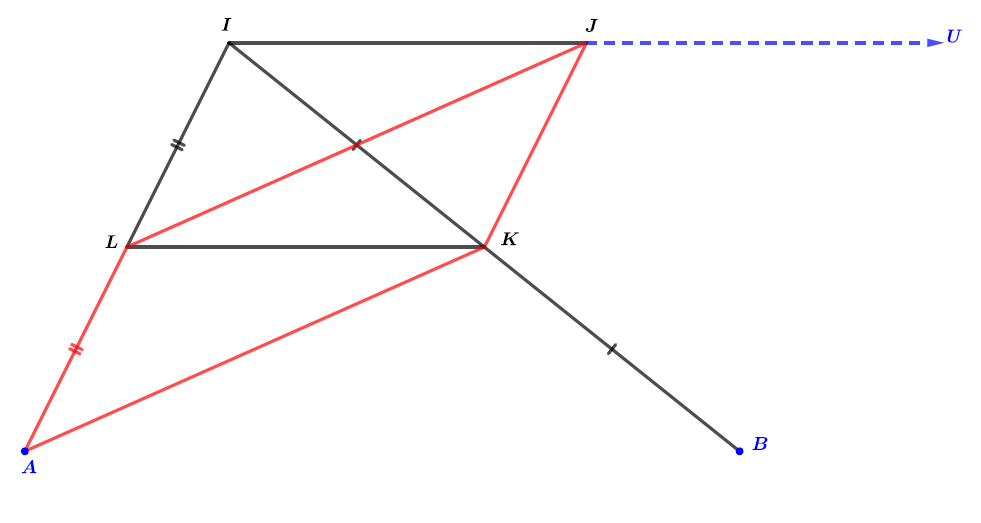
Nous savons également que est un parallélogramme ce qui nous permet d'écrire .
Il en résulte donc que : . Cette égalité vectorielle permet de démontrer que le quadrilatère est un parallélogramme .

Question 4
Que représente le point pour le segment . Justifier
Correction
Nous avons démontré que d'après la question .
D'après la question , le quadrilatère est un parallélogramme ce qui signifie que .
Cela nous permet donc d'écrire que . Il en résulte donc que le point est bien le segment .
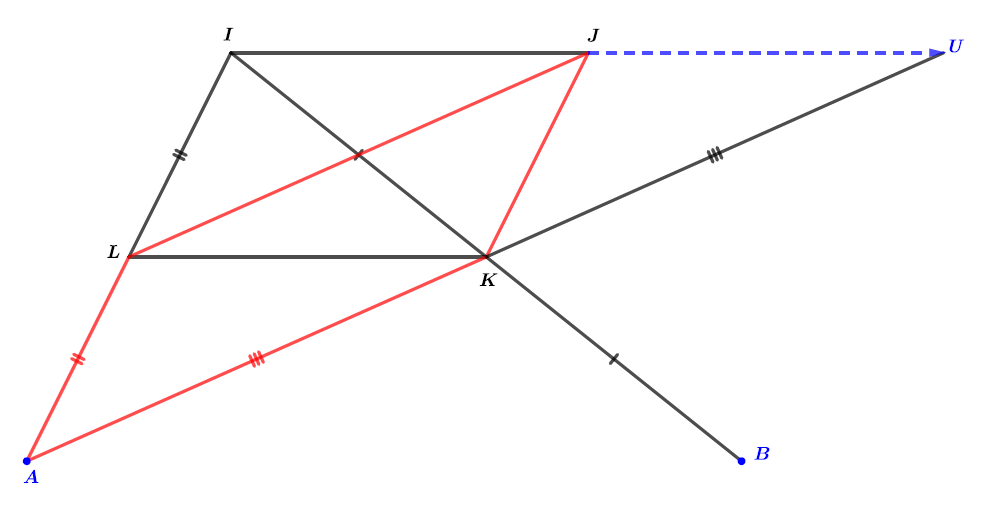
D'après la question , le quadrilatère est un parallélogramme ce qui signifie que .
Cela nous permet donc d'écrire que . Il en résulte donc que le point est bien le segment .

Question 5
Quel est la nature du quadrilatère . Justifier.
Correction
D'après la question , le point est le milieu du segment .
De plus, parmi les hypothèses, le point est le milieu du segment .
Les segments et sont les diagonales du quadrilatère .
est un quadrilatère .
Il en résulte donc que le quadrilatère est un parallélogramme.
De plus, parmi les hypothèses, le point est le milieu du segment .
Les segments et sont les diagonales du quadrilatère .
est un quadrilatère .
Il en résulte donc que le quadrilatère est un parallélogramme.

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.