Vecteurs du plan : première Partie
Calculer les coordonnées du milieu d'un segment - Exercice 1
10 min
15
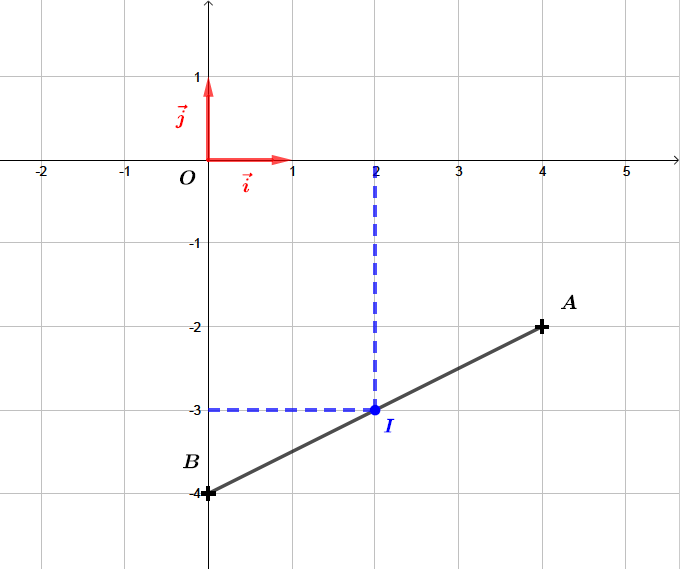
Soit un repère orthonormé du plan. On considère les points ; .
Question 1
Déterminer les coordonnées du milieu du segment .
Correction
Soit un repère orthonormé du plan et deux points et
Il vient alors que :- Les coordonnées du milieu du segment sont : et
équivaut successivement à :
Les coordonnées du milieu du segment sont
Question 2
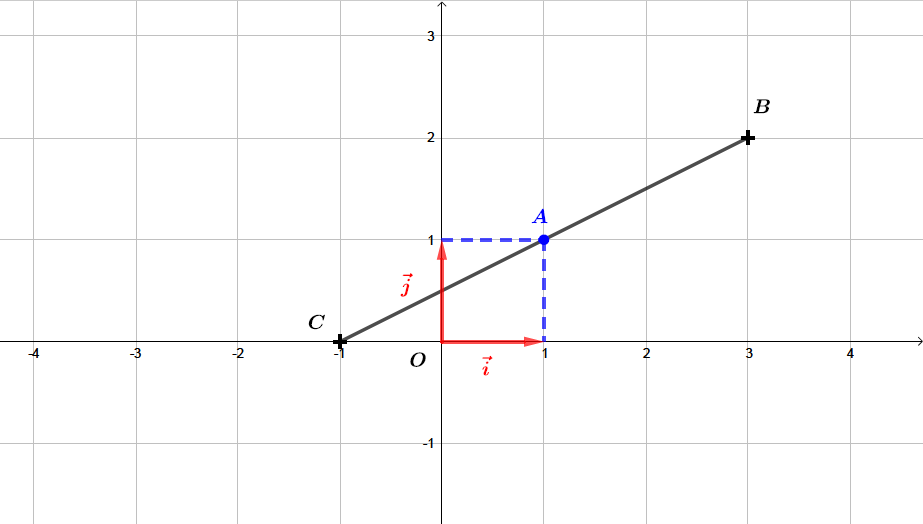
Soit un repère orthonormé du plan. On considère les points ; .
Déterminer les coordonnées du milieu du segment .
Correction
Soit un repère orthonormé du plan et deux points et
Il vient alors que :- Les coordonnées du milieu du segment sont : et
équivaut successivement à :
Les coordonnées du milieu du segment sont
Question 3
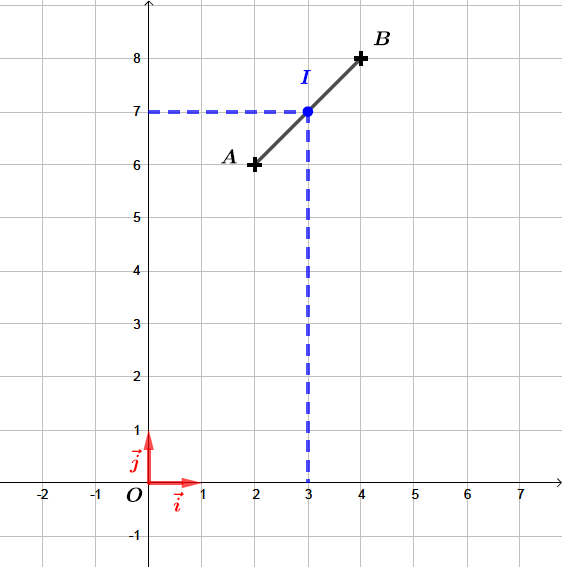
Soit un repère orthonormé du plan. On considère les points ; .
Déterminer les coordonnées du milieu du segment .
Correction
Soit un repère orthonormé du plan et deux points et
Il vient alors que :- Les coordonnées du milieu du segment sont : et
équivaut successivement à :
Les coordonnées du milieu du segment sont
Question 4
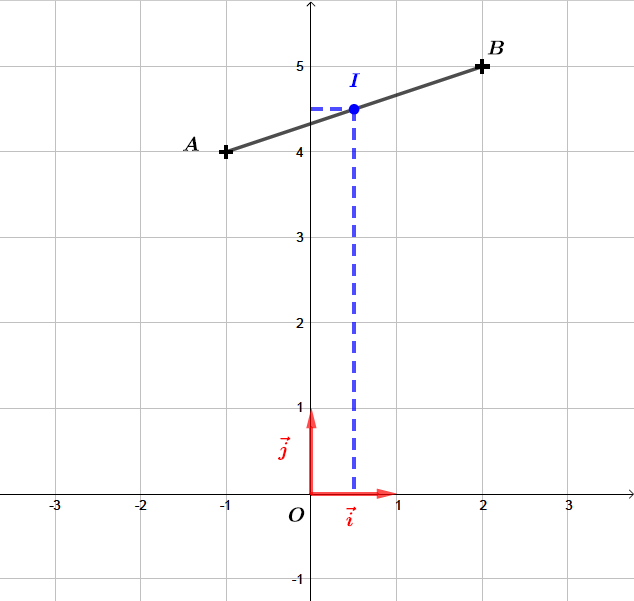
Soit un repère orthonormé du plan. On considère les points ; .
Déterminer les coordonnées du milieu du segment .
Correction
Soit un repère orthonormé du plan et deux points et
Il vient alors que :- Les coordonnées du milieu du segment sont : et
équivaut successivement à :
Les coordonnées du milieu du segment sont