Nouveau

🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches  →

Tchat avec un prof

🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir  →

Savoir calculer une moyenne - Exercice 1

8 min
15
Question 1
On définit la série statistique suivante :

Déterminer une valeur approchée, à 10−210^{-2} près, de la moyenne de cette série statistique.

Correction
La moyenne d'une série statistique est le réel, noté x‾\overline{x}, tel que :
x‾=n1x1+n2x2+n3x3+…+npxpN\overline{x}=\frac{n_{1} x_{1} +n_{2} x_{2} +n_{3} x_{3} +\ldots +n_{p} x_{p} }{N}
Ici, NN correspond à l'effectif total, c'est à dire : N=10+5+13+15=43N=10+5+13+15=43.
Il vient alors que :
x‾=0×10+1×5+2×13+3×1543\overline{x}=\frac{0\times 10+1\times 5+2\times 13+3\times 15}{43}
x‾=7643\overline{x}=\frac{76}{43}
x‾≈1,77\overline{x}\approx1,77
.
Question 2
On définit la série statistique suivante :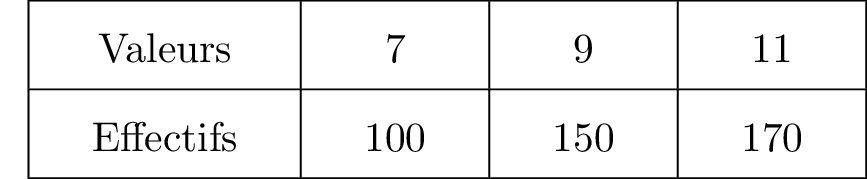

Déterminer une valeur approchée, à 10−210^{-2} près, de la moyenne de cette série statistique.

Correction
La moyenne d'une série statistique est le réel, noté x‾\overline{x}, tel que :
x‾=n1x1+n2x2+n3x3+…+npxpN\overline{x}=\frac{n_{1} x_{1} +n_{2} x_{2} +n_{3} x_{3} +\ldots +n_{p} x_{p} }{N}
Ici, NN correspond à l'effectif total, c'est à dire : N=100+150+170=420N=100+150+170=420.
Il vient alors que :
x‾=7×100+9×150+11×170420\overline{x}=\frac{7\times 100+9\times 150+11\times 170}{420}
x‾=3920420\overline{x}=\frac{3920}{420}
x‾≈9,33\overline{x}\approx9,33
.

Signaler une erreur

Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.

Connecte-toi ou crée un compte pour signaler une erreur.