Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
35 min
55
Une machine est programmée pour fabriquer des boules de billard dont le diamètre doit être de cm . Pour cela, l'opérateur règle la machine sur cette valeur. On observe toutefois les variations dans les diamètres de boules de billard. Un échantillon de boules est prélevé afin de contrôler la machine. Les résultats sont dans le tableau suivant :
Question 1

Quelle est la population étudiée?
Correction
La population étudiée ici : les boules de billard.
Question 2
Quel est le caractère observé?
Correction
Le caractère observé : le diamètre des boules de billard.
Question 3
Quelle est l'étendue de cette série?
Correction
Question 4
Calculer le diamètre moyen .
Correction
La moyenne d'une série statistique est le réel, noté , tel que :
Nous savons que l'effectif total est . Il vient alors que :.
Question 5
Si la machine est bien réglée, la moyenne des diamètres d'un échantillon d'effectif doit appartenir à l'intervalle . Est ce bien le cas?
Correction
D'après la question , nous voyons bien que .
La machine est donc bien réglée.
La machine est donc bien réglée.
Question 6
Quelle est la médiane de cette série? Justifier, puis donner une interprétation concrète de cette valeur.
Correction
Nous allons dans un premier temps rajouter la ligne des effectifs cumulés croissant.
 Pour déterminer la médiane, on commence par calculer ce qui donne .
Pour déterminer la médiane, on commence par calculer ce qui donne .
Comme est pair, on agit de la sorte.
On indique que la médiane correspond à :
où ici
La ème valeur de la série est : .
La ème valeur de la série est : .
Ainsi :

Comme est pair, on agit de la sorte.
On indique que la médiane correspond à :
où ici
La ème valeur de la série est : .
La ème valeur de la série est : .
Ainsi :
La médiane est la plus petite valeur de la série telle qu‘au moins des données soient inférieures à .
Autrement dit , il y a au moins des boules de billard qui ont un diamètre inférieures ou égale à cm.Question 7
Donner les valeurs des quartiles et .
Correction

En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Nous savons que Ainsi :
.
(Dans la ligne des ECC on recherche la valeur si elle n'apparait pas on prend la valeur supérieur ici on prend et donc cela correspond à cm)
Ainsi :
.
(Dans la ligne des ECC on recherche la valeur et ici nous avons bien la valeur et donc cela correspond à cm)
Question 8
Construire la boite à moustaches de cette série.
Correction
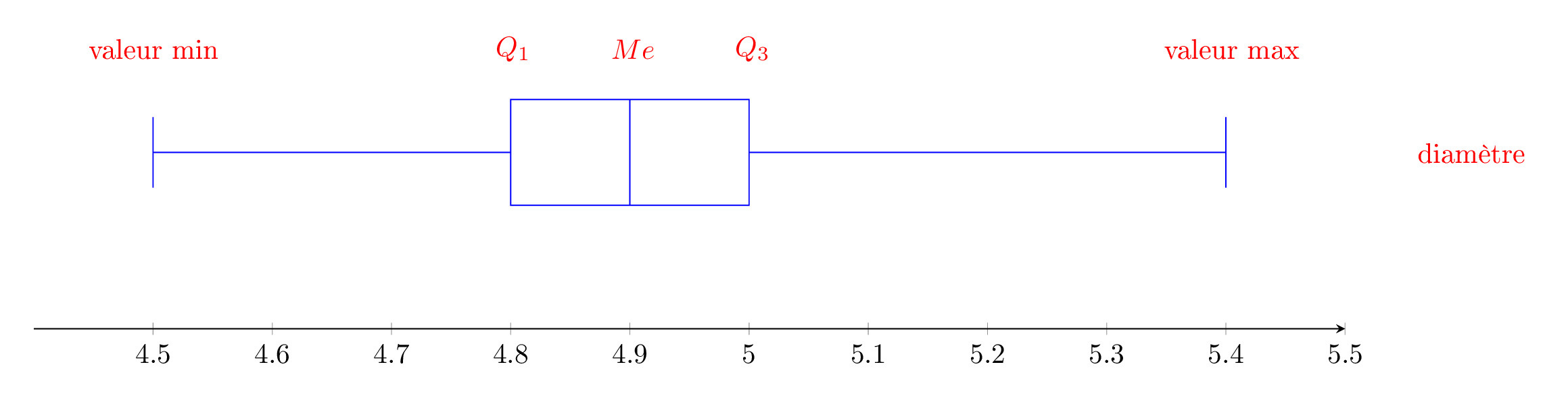
Question 9
Compléter le tableau suivant : ( en regroupant par classes les valeurs initiales ).


Correction
Nous allons reprendre le tableau initial et nous avons mis en couleurs les diamètres appartenant au classes souhaitées. 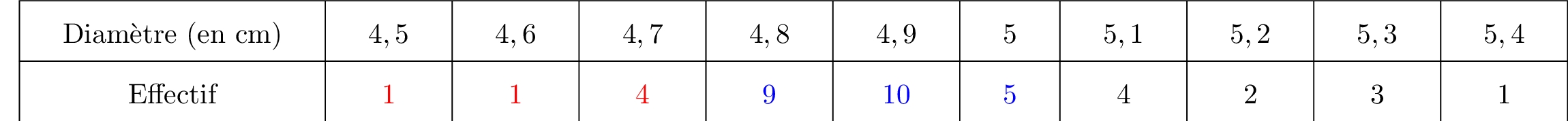 Il vient alors que :
Il vient alors que : 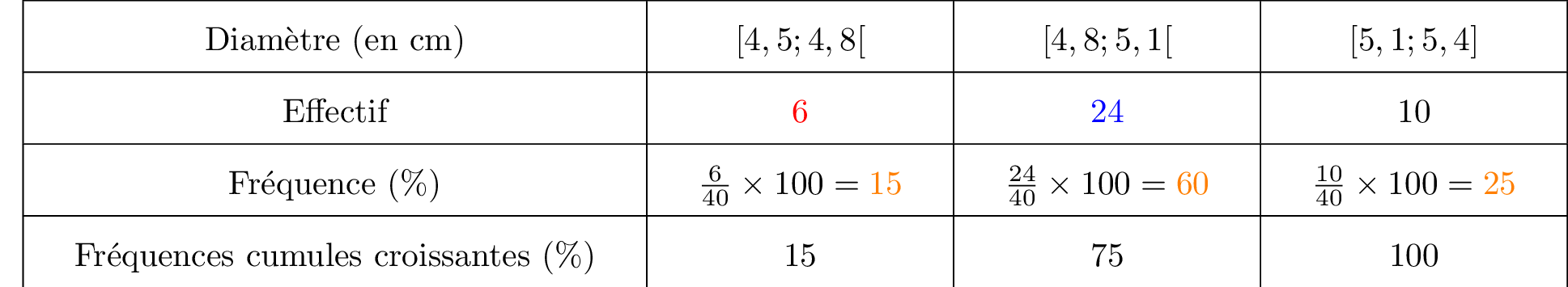
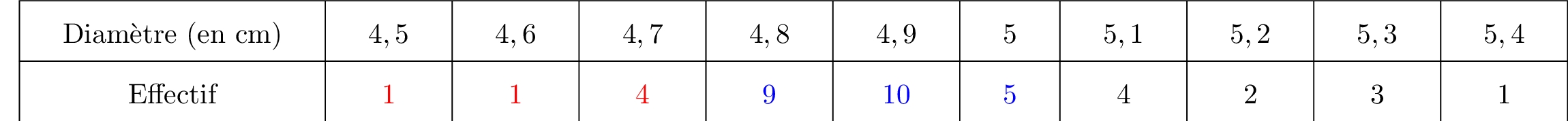
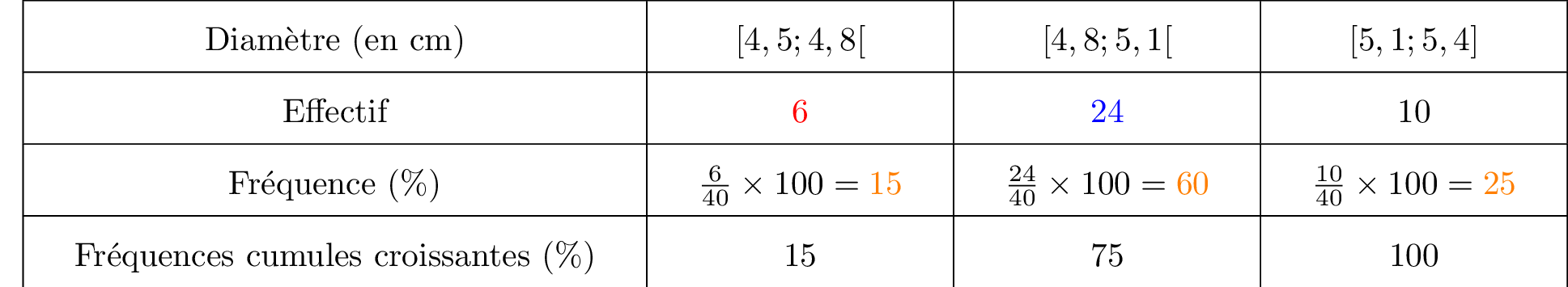
Question 10
Quelle est la classe modale?
Correction
La classe modale correspond à la classe qui dispose du plus grand effectif.
Ici, la classe modale est alors :
Ici, la classe modale est alors :
Question 11
En utilisant les regroupements par classes, calculer le diamètre moyen
Correction
Nous allons reproduire le tableau qui utilise les classes et nous allons y référencer le centre de la classe afin de faire le calcul du diamètre moyen.
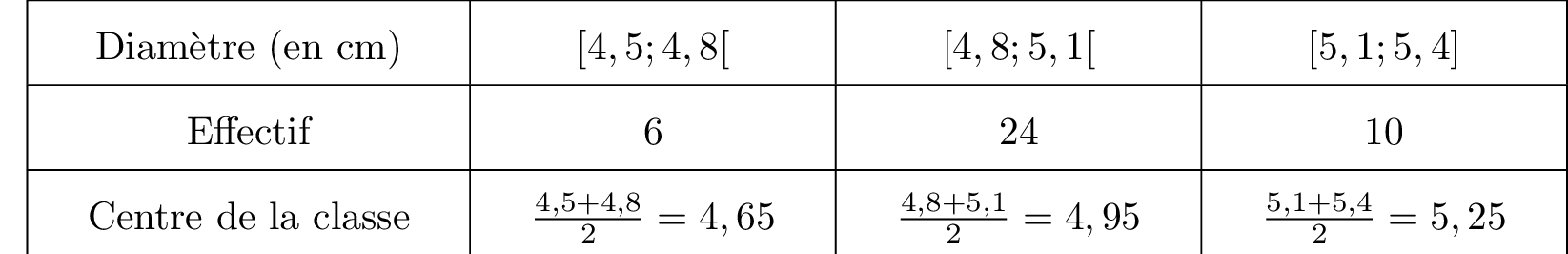
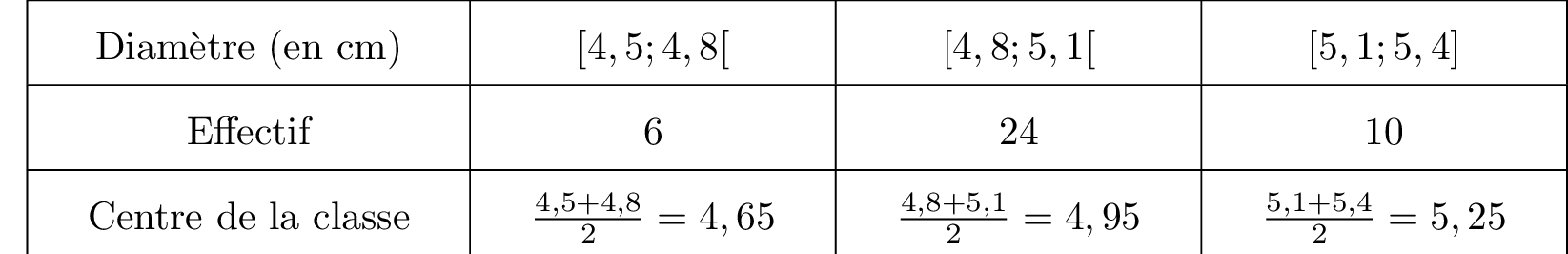
.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.