Exercices types : ème partie - Exercice 1
15 min
25
Question 1
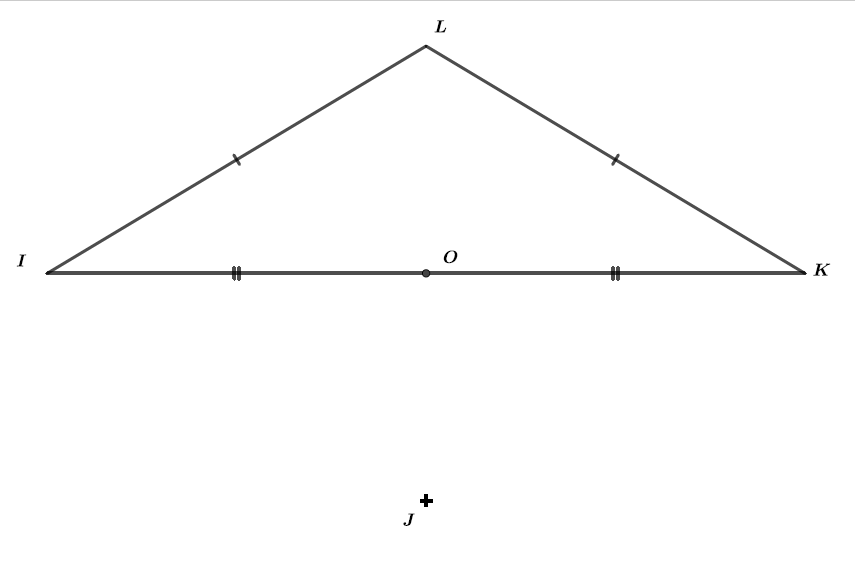
On considère un triangle isocèle en , est le milieu de . est le symétrique de par rapport au point .
Faire une figure que l'on complétera au fur et à mesure des questions.
Correction
Question 2
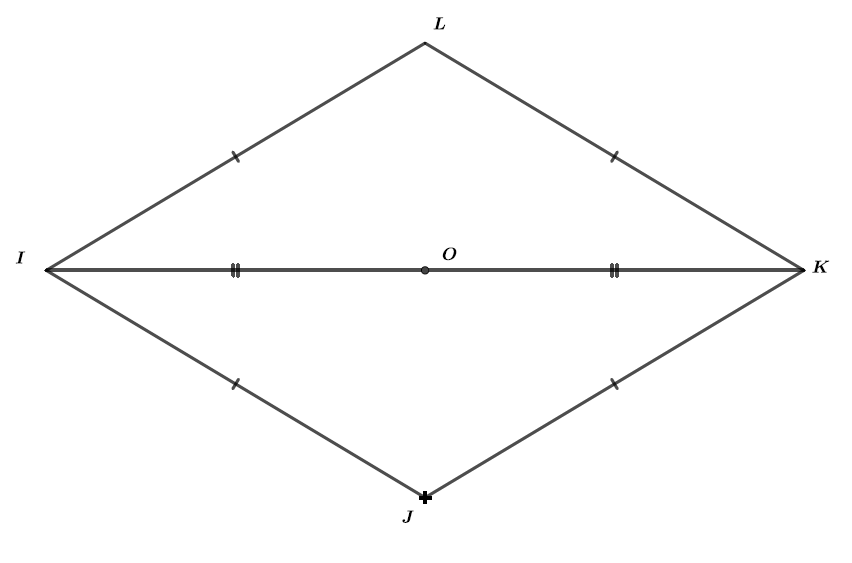
Justifier que le quadrilatère est un losange.
Correction
et sont les diagonales du quadrilatère
On sait que :
est le milieu du segment
est le symétrique de par rapport au point . On peut donc en conclure que est le milieu du segment .
Les diagonales du quadrilatère se coupent en leur milieu, on peut donc en conclure dans un premier temps que le quadrilatère est un parallélogramme.
De plus car le triangle est isocèle en .
Or dans le parallélogramme on a
Par conséquent le paraléllogramme a deux côtés consécutifs de même longueur, donc est un losange.
On sait que :
Les diagonales du quadrilatère se coupent en leur milieu, on peut donc en conclure dans un premier temps que le quadrilatère est un parallélogramme.
De plus car le triangle est isocèle en .
- Un parallélogramme qui a deux côtés consécutifs de même longueur est un losange.
Par conséquent le paraléllogramme a deux côtés consécutifs de même longueur, donc est un losange.
Question 3
est la droite parallèle à passant par le point . Démontrer que est perpendiculaire à la droite .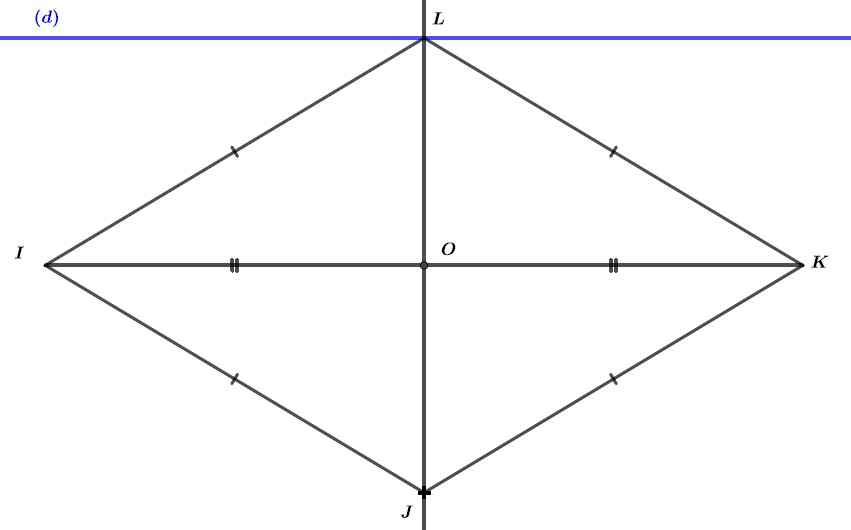
Correction
On sait que est un losange.
Par conséquent on peut en déduire que
On sait que est la droite parallèle à passant par le point
Par conséquent puisque et que , on peut donc en conclure que
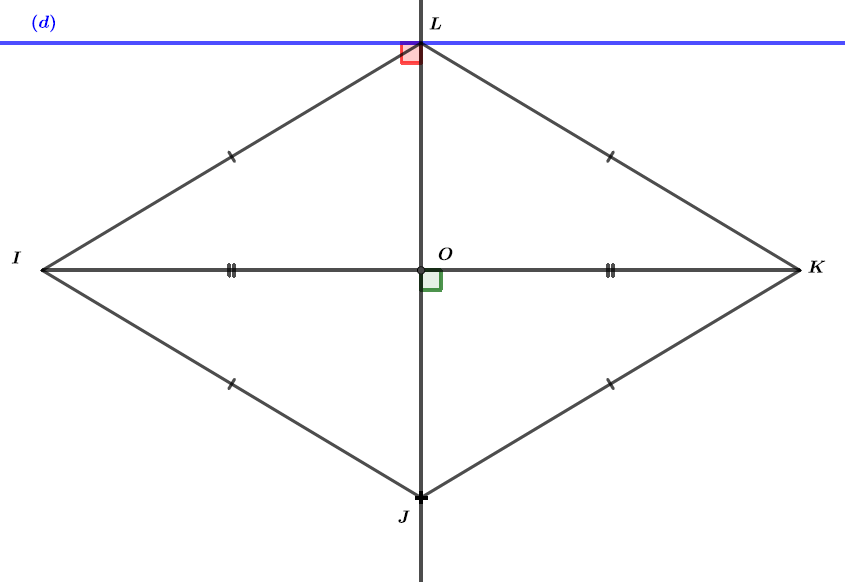
- Les diagonales d'un losange se coupent perpendiculairement.
On sait que est la droite parallèle à passant par le point
- Si deux droites sont parallèles, toute perpendiculaire à l'une est perpendiculaire à l’autre.
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.