Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
20 min
40
Une société qui souhaite commercialiser des Tee-shirts propose des frais de création à euros. Ensuite, la production pour chaque Tee-shirt est de euros.
Question 1
Déterminer le coût de production , noté , pour tee-shirts.
Correction
Les frais de création sont de euros et ensuite chaque Tee-shirt coûtera euros.
Il en résulte donc que :
Il en résulte donc que :
Question 2
Chaque tee-shirt est vendu euros. Calculer la recette, noté , pour tee-shirts vendus.
Correction
Chaque tee-shirt étant vendu euros, il en résulte donc que que l'on peut écrire également
Question 3
Calculer le bénéfice pour tee-shirts produits et vendus. Le bénéfice est égal à la recette moins les coûts de production.
Correction
On nous indique que le bénéfice est égal à la recette moins les coûts de production.
Cela signifie donc que :
. Ici , nous n'oublions pas de changer les signes, à l'étape suivante car nous avons le signe moins devant la parenthèse.
Cela signifie donc que :
. Ici , nous n'oublions pas de changer les signes, à l'étape suivante car nous avons le signe moins devant la parenthèse.
Question 4
Déterminer le sens de variation de la fonction .
Correction
Nous savons que :
Soient et deux réels.Ici, le coefficient directeur vaut . Il en résulte donc que la fonction est une fonction croissante.
Le tableau de variation de la fonction est donnée ci-dessous :
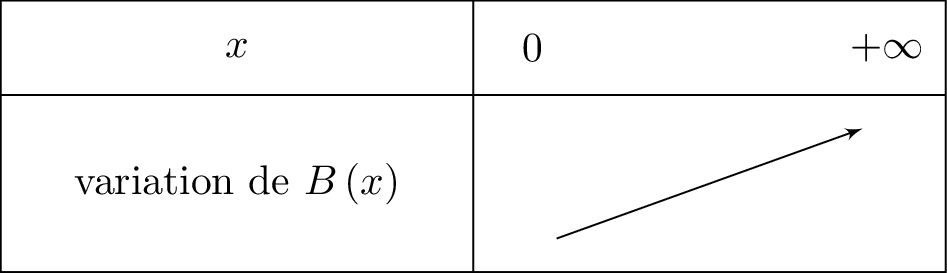 Ici nous travaillons sur l'intervalle car une production de tee-shirts n'est vrai que pour des positifs.
Ici nous travaillons sur l'intervalle car une production de tee-shirts n'est vrai que pour des positifs.
Soient et deux réels.
- Si est positif, la fonction affine définie sur par est croissante.
- Si est négatif, la fonction affine définie sur par est décroissante.
Le tableau de variation de la fonction est donnée ci-dessous :

Question 5
Déterminer le tableau de signe de la fonction .
Correction
1ère étape : Résoudre l'équation
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
3ème étape : Dresser le tableau de signe de .
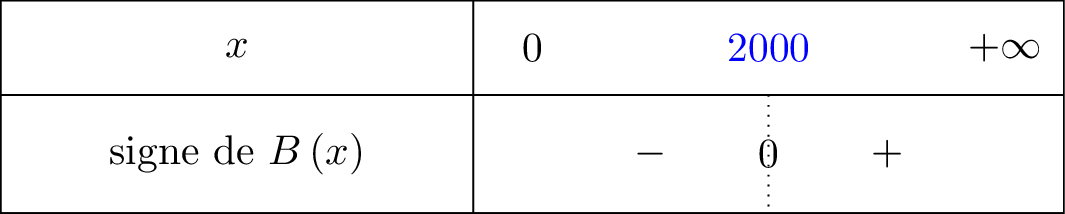 Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
Nous remettons ici l'information vue à la deuxième étape pour bien comprendre. Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)
équivaut successivement à :
2ème étape : Donner le sens de variation de la fonction .
En italique ce sont des phrases explicatives qui ne doivent pas apparaitre sur vos copies, elles servent juste à vous expliquer le raisonnement.
Soit est une fonction affine croissante car son coefficient directeur . (Cela signifie que la fonction MONTE donc on commencera dans la ligne par le signe et dès que l'on dépasse la valeur on mettra le signe dans le tableau de signe.)3ème étape : Dresser le tableau de signe de .
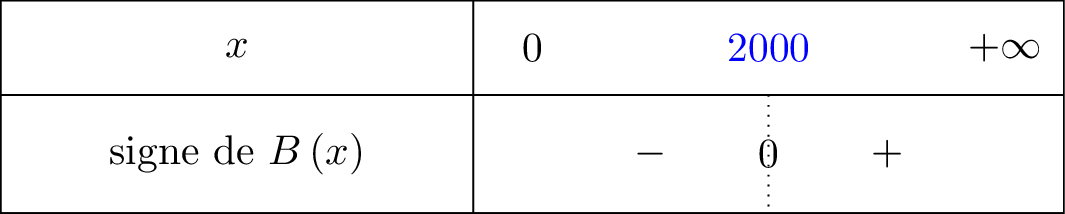
Question 6
A partir de combien de tee-shirts vendus que la société réalisera un bénéfice?
Correction
On réalisera un bénéficie lorsque la fonction sera positive.
Nous redonnons ci-dessous le tableau de signe de la fonction obtenue à la question .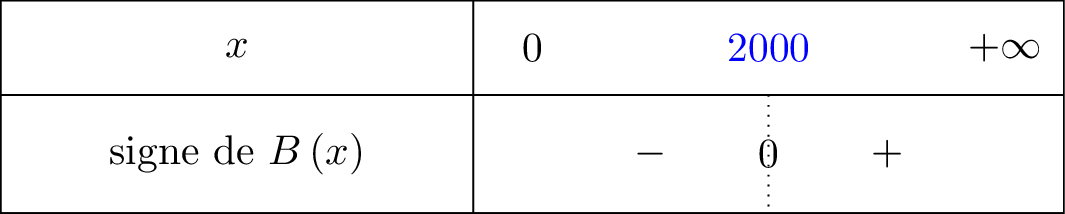 A partir de tee-shirts, la société réalise un bénéfice.
A partir de tee-shirts, la société réalise un bénéfice.
Nous redonnons ci-dessous le tableau de signe de la fonction obtenue à la question .
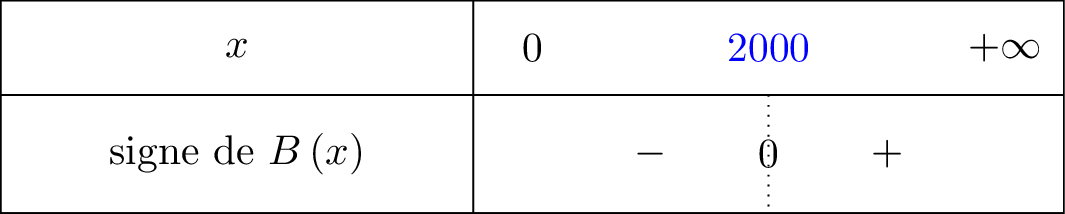
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.