Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Comment lire graphiquement une équation de droite - Exercice 1
20 min
30
Question 1
Dans chaque cas où la droite représentée ci-dessus, est la courbe représentative d’une fonction, déterminer la fonction affine associée.
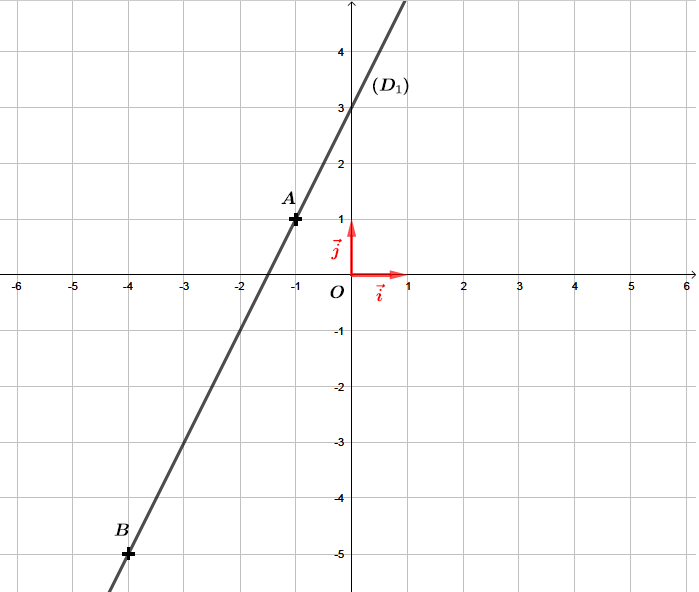
Correction
La droite est une fonction affine de la forme .
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que .
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme : 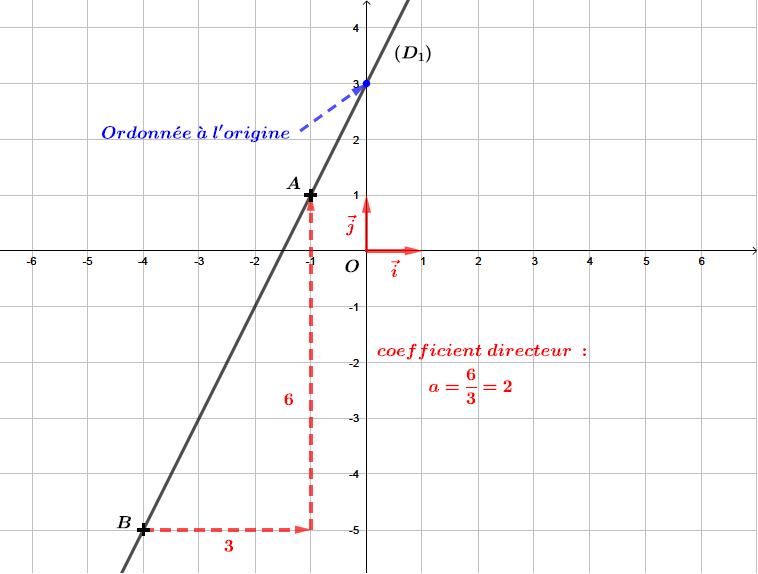
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme :

Question 2
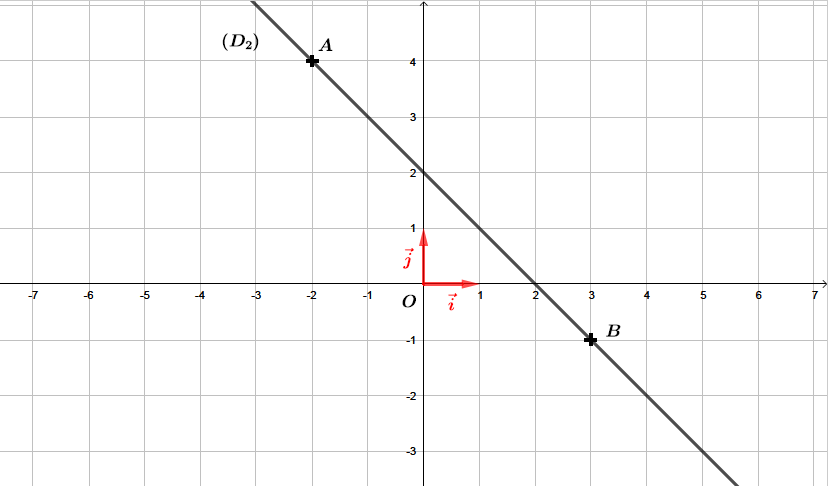
Correction
La droite est une fonction affine de la forme .
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que .
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme : 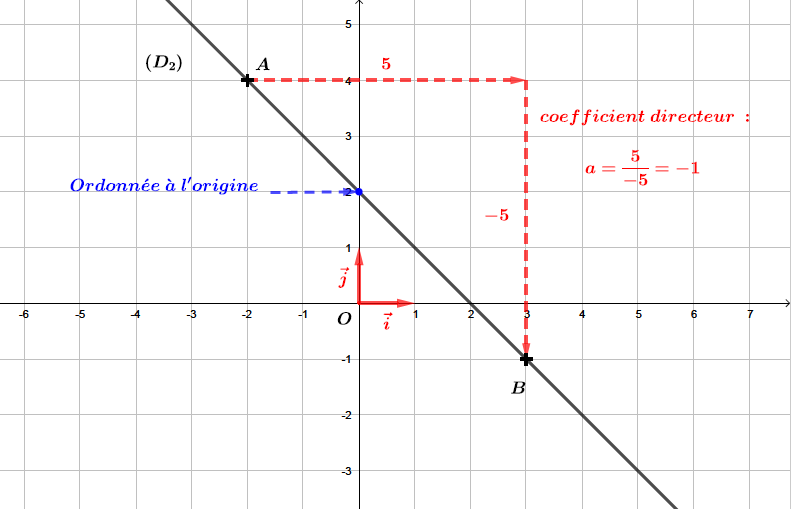
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme :

Question 3
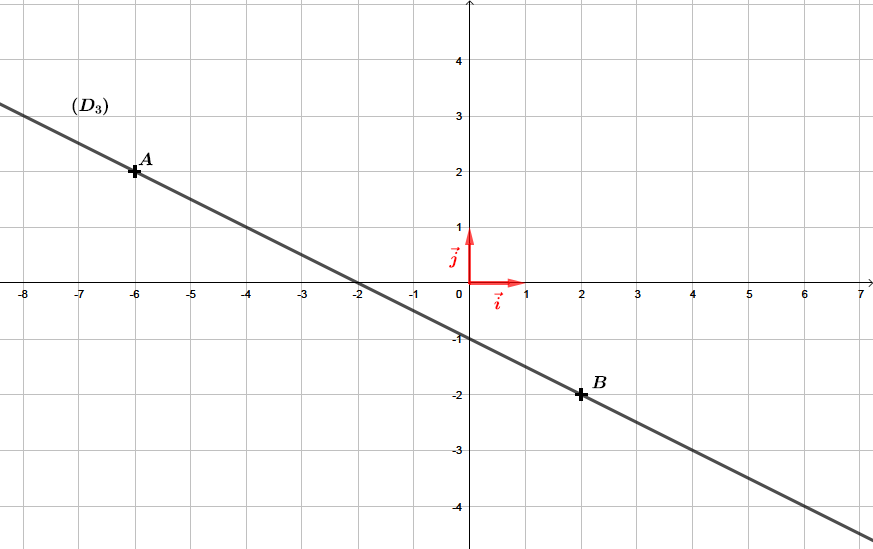
Correction
La droite est une fonction affine de la forme .
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que .
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme : 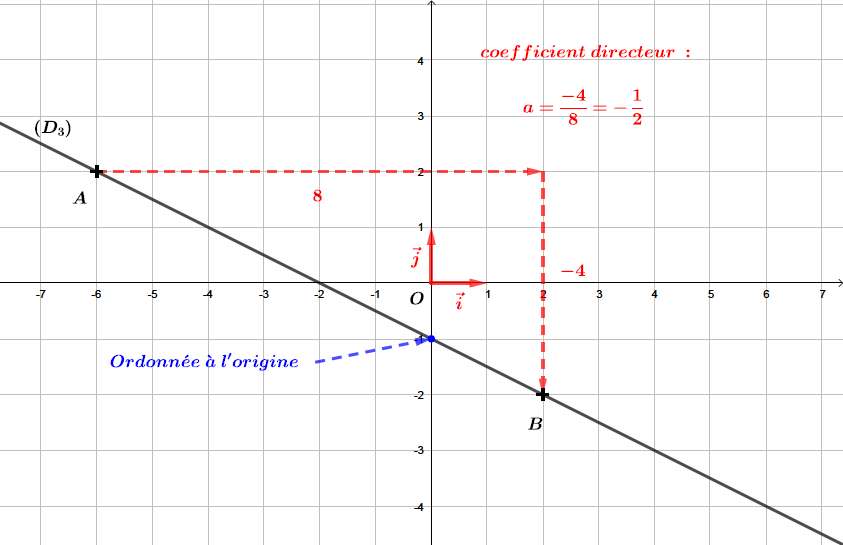
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme :

Question 4
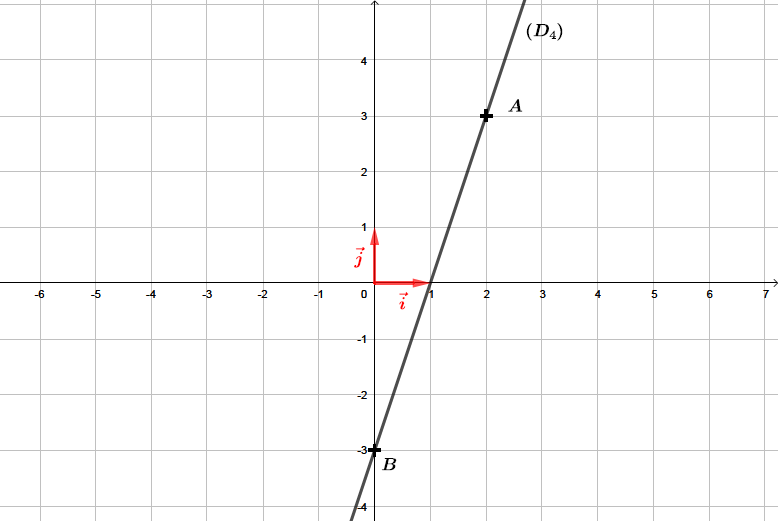
Correction
La droite est une fonction affine de la forme .
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que .
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme : 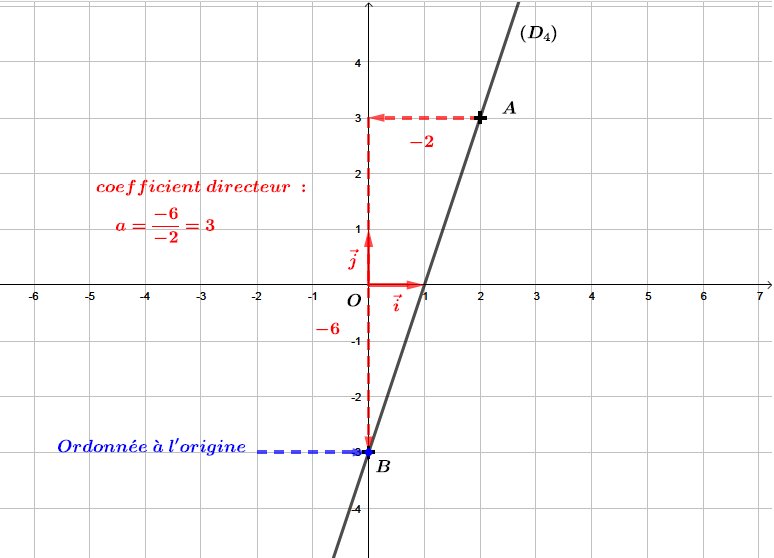
ère étape : Déterminer l'ordonnée l'origine .
L'ordonnée à l'origine est le point d'intersection entre l'axe des ordonnées et la droite .
Nous pouvons facilement lire ici que
ème étape : Déterminer le coefficient directeur .
Pour déterminer le coefficient directeur de la droite , nous remarquons que les points et appartiennent à la droite . Nous pouvons donc calculer le coefficient directeur de la droite à l'aide de la formule suivante :
Finalement, la fonction affine associée à la droite est de la forme :

Question 5
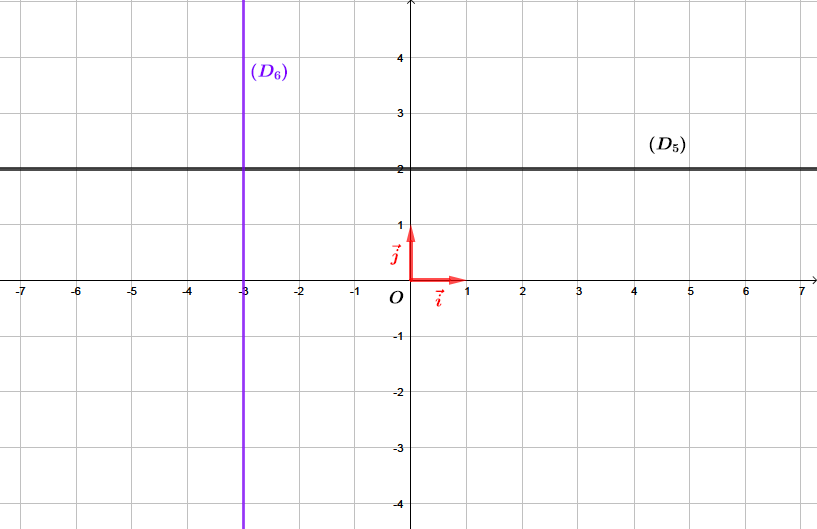
Correction
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.