Fonction polynôme du second degré : $f\left(x\right)=ax^{2} +bx+c$

Exercices types : 1ère partie - Exercice 2

15 min
25
Question 1
Un cordonnier fabrique des chaussures qu’il met en vente. On suppose que toutes les chaussures fabriquées sont vendus. Le cordonnier veut faire une étude sur la production d’un nombre de chaussures compris entre 00 et 6060. Il estime que le coût de production en euros de xx chaussures fabriqués est modélisé par la fonction CC dont l’expression est C(x)=x2−10x+500C\left(x\right) = x^{2} - 10x + 500 où x∈[0;60]x\in\left[0;60\right].
Chaque chaussure est vendue 5050 euros.

Quelle est la recette pour xx chaussures vendues. On notera R(x)R\left(x\right) la recette pour xx chaussures vendues.

Correction
Nous allons faire plusieurs simulations. On sait que l'on vend chaque chaussure 5050 euros.
  • Pour la vente, par exemple de 66 chaussures, la recette sera : 50×6=30050\times6=300
  • Pour la vente, par exemple de 1010 chaussures, la recette sera : 50×10=50050\times10=500
  • Pour la vente, par exemple de 1212 chaussures, la recette sera : 50×12=60050\times12=600
  • Finalement, pour la vente de xx chaussures, la recette sera : 50×x=50x50\times x=50x
    • Soit :
    R(x)=50xR\left(x\right)=50x
    Question 2
    Le bénéfice est égal à la différence entre la recette et le coût de fabrication.

    Montrer que le bénéfice B(x)B\left(x\right) réalisé par la fabrication et la vente de xx chaussures est défini par : B(x)=−x2+60x−500B\left(x\right)=-x^{2}+60x-500

    Correction
    On nous indique que le bénéfice est égal à la différence entre le prix de vente et le coût de fabrication.
    Il en résulte donc que :
    B(x)=R(x)−C(x)B\left(x\right)=R\left(x\right)-C\left(x\right) équivaut successivement à :
    B(x)=50x−(x2−10x+500)B\left(x\right)=50x-\left(x^{2} - 10x + 500 \right) . Nous allons changer les signes de la parenthèse à la prochaine étape ci-dessous.
    B(x)=50x−x2+10x−500B\left(x\right)=50x-x^{2}+10x-500
    B(x)=−x2+60x−500B\left(x\right)=-x^{2}+60x-500
    Question 3

    Dresser le tableau de variation de la fonction BB.

    Correction
    Pour déterminer le bénéfice maximal, nous allons commencer par donner la forme canonique de : B(x)=−x2+60x−500B\left(x\right)=-x^{2}+60x-500

    Toute fonction polynôme ff de degré 22 définie sur R\mathbb{R} par f(x)=ax2+bx+cf\left(x\right)=ax^{2}+bx+c avec a≠0a\ne0, peut s'écrire sous la forme :
    • f(x)=a(x−α)2+βf\left(x\right)=a\left(x-\alpha \right)^{2} +\beta avec α=−b2a\alpha =\frac{-b}{2a} et β=f(α)\beta =f\left(\alpha \right)
    1ère étape : On définit les valeurs aa, bb et cc.
    • a=a= nombre devant x2x^{2} d'où a=−1a=-1
    • b=b= nombre devant xx d'où b=60b=60
    • c=c= nombre seul d'où c=−500c=-500
    2ème étape : Calcul de α=−b2a\alpha =\frac{-b}{2a}
    Il vient alors que : α=−602×(−1)\alpha =\frac{-60}{2\times\left(-1\right)} d'où :
    α=30\alpha =30

    3ème étape : Calcul de β=B(α)\beta =B\left(\alpha \right)
    Il vient alors que :
    β=B(30)\beta =B\left(30 \right)
    β=−(30)2+60×30−500\beta =-\left(30\right)^{2}+60\times30-500
    β=−900+1800−500\beta =-900+1800-500
    β=400\beta =400

    Ainsi, pour tout réel xx, la forme canonique est : f(x)=a(x−α)2+βf\left(x\right)=a\left(x-\alpha \right)^{2} +\beta ce qui nous donne : B(x)=−1(x−30)2+400B\left(x\right)=-1\left(x-30 \right)^{2}+400.
    Autrement dit :
    B(x)=−(x−30)2+400B\left(x\right)=-\left(x-30\right)^{2}+400
    .
    Maintenant, que nous avons la forme canonique de la fonction BB, nous allons pouvoir dresser le tableau de variation de BB.
    • Soit la forme canonique f(x)=a(x−α)2+βf\left(x\right)=a\left(x-\alpha \right)^{2} +\beta avec α=−b2a\alpha =\frac{-b}{2a} et β=f(α)\beta =f\left(\alpha \right) . Si a<0a<0, la parabole est tournée vers le bas et le tableau de variation est comme suit :
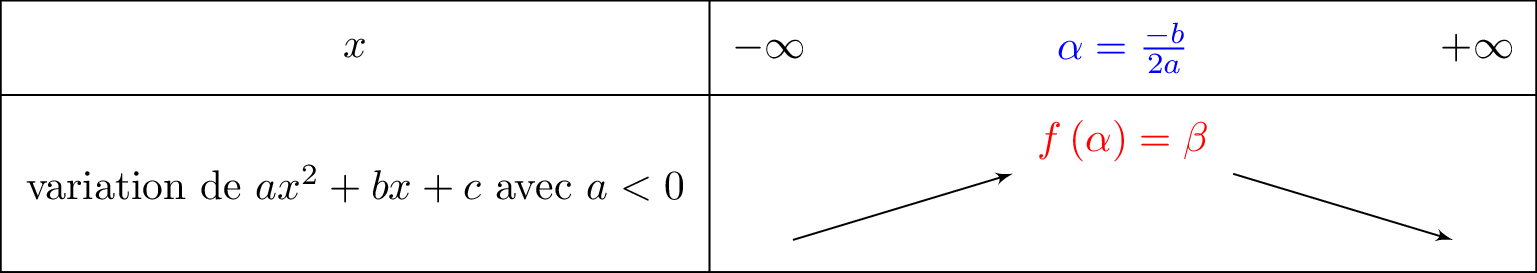
    Comme a=−1<0a=-1<0, la parabole est tournée vers le bas. Il en résulte donc que :
    Question 4

    En déduire le nombres de chaussures à vendre pour réaliser un bénéfice maximum. Quel est alors ce bénéfice maximum?

    Correction
    En reprenant le tableau de variation de BB est :
    Pour une production de 3030 chaussures, le bénéfice maximal est alors de 400400 euros.