Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Résolution graphique - Exercice 1
15 min
25
Question 1
A l'aide de la représentation de la fonction carré, résoudre graphiquement les inéquations suivantes :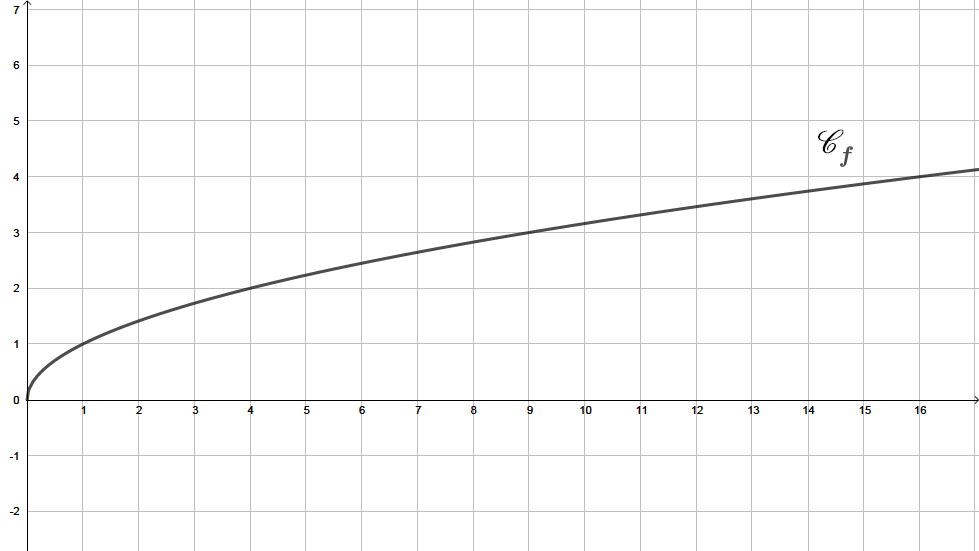

Correction
Sur le graphique ci-dessus, nous avons tracé la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont au dessus ou sur la droite d'équation .
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : 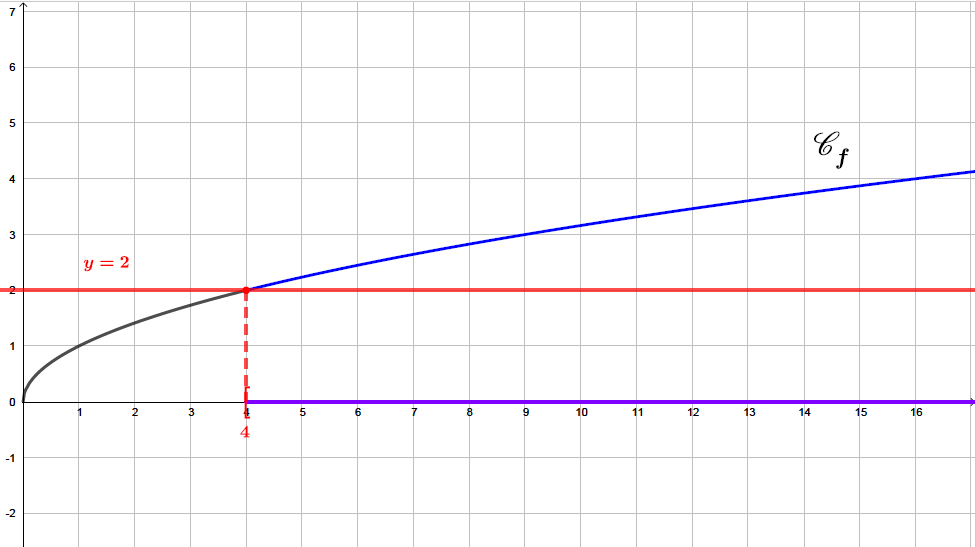
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

Question 2
Correction
Sur le graphique ci-dessus, nous avons tracé la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont strictement en dessous de la droite d'équation .
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : 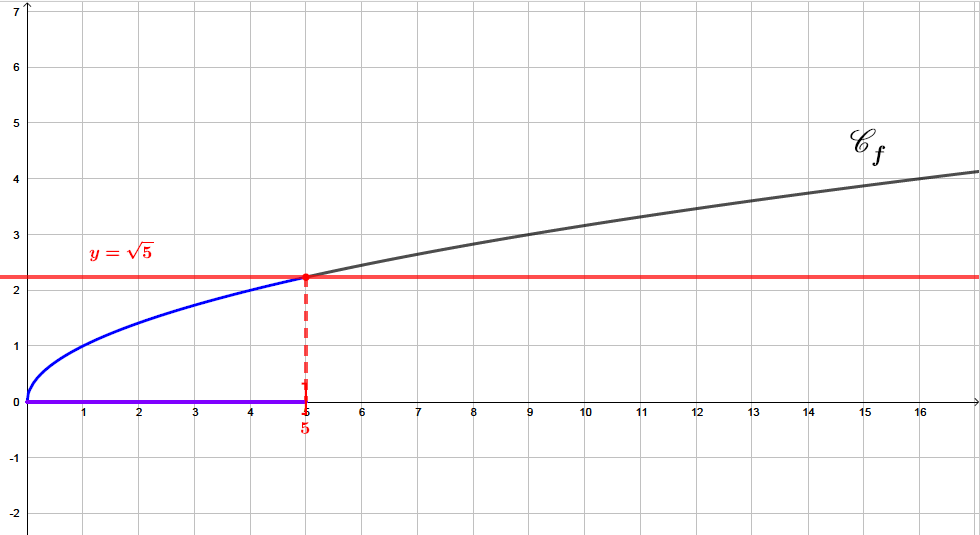
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

Question 3
Correction
Sur le graphique ci-dessus, nous avons tracé la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont au dessus ou sur la droite d'équation .
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : 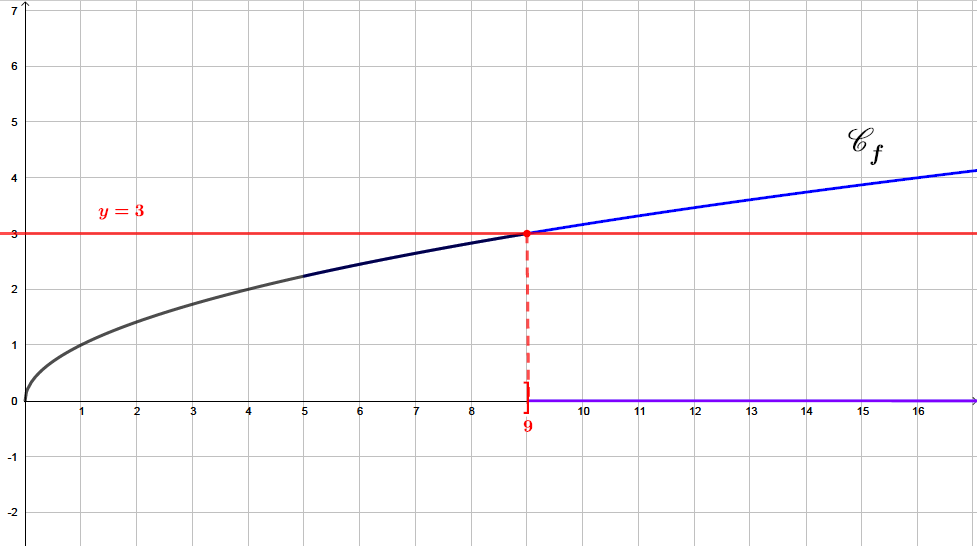
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

Question 4
Correction
Sur le graphique ci-dessus, nous avons tracé la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont strictement en dessous de la droite d'équation .
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi : 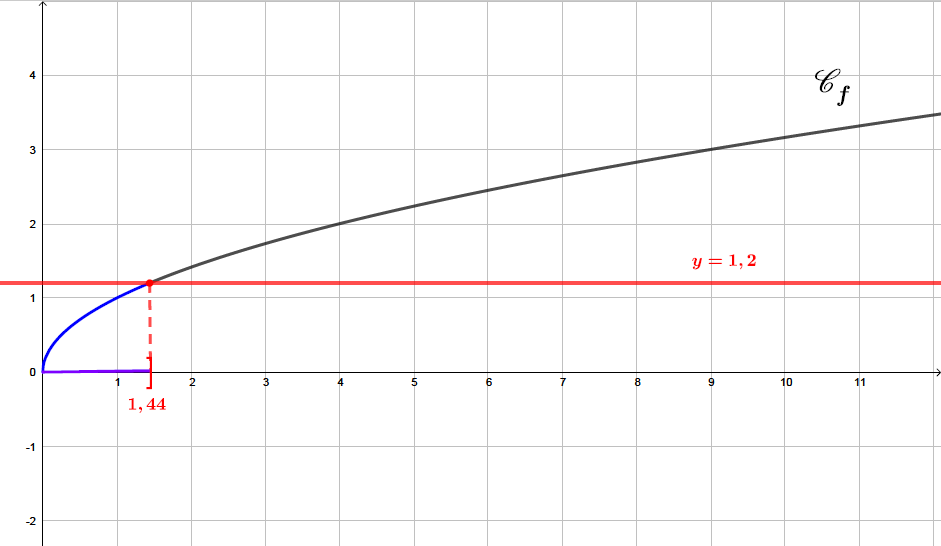
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

Question 5
Correction
Sur le graphique ci-dessus, nous avons tracé la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont strictement en dessous de la droite d'équation .
La fonction racine carrée est ce qui signifie que la racine carrée ne peut pas être inférieure à une valeur négative.
Ainsi :
La fonction racine carrée est ce qui signifie que la racine carrée ne peut pas être inférieure à une valeur négative.
Ainsi :

Question 6
Correction
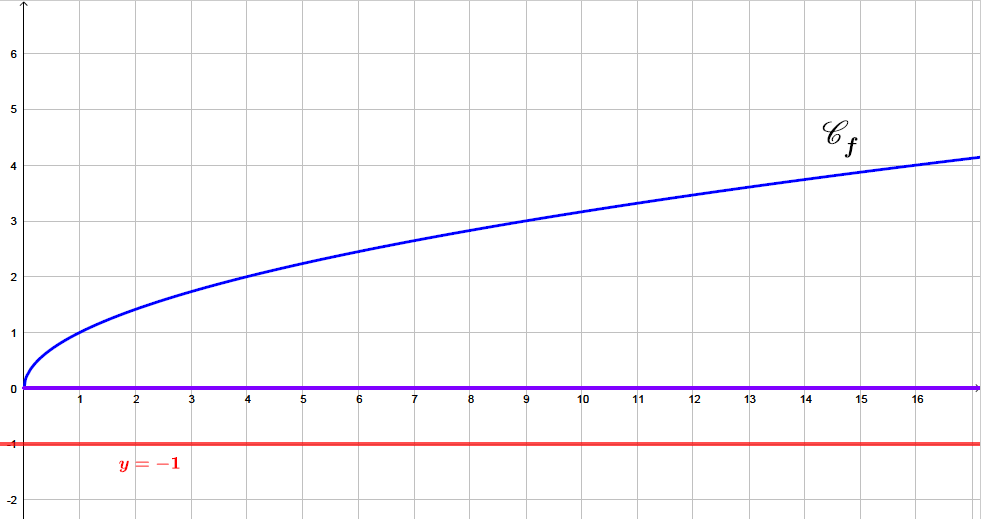
Sur le graphique ci-dessus, nous avons tracé la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont strictement en dessous de la droite d'équation
La fonction racine carrée est ce qui signifie que la racine carrée ne peut pas être inférieure à une valeur négative.
Ainsi :
La fonction racine carrée est ce qui signifie que la racine carrée ne peut pas être inférieure à une valeur négative.
Ainsi :

Question 7
Correction
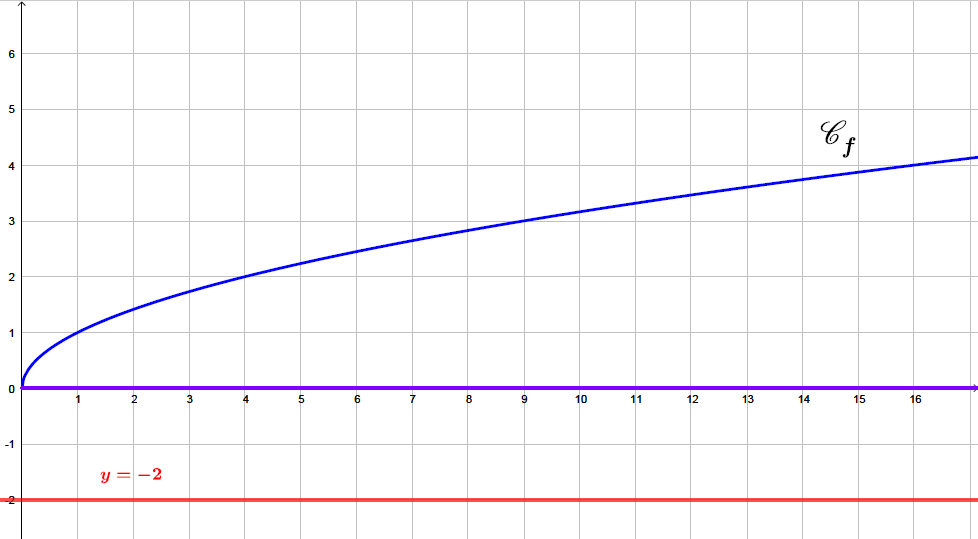
Sur le graphique ci-dessus, nous avons tracé la droite . Pour résoudre l'inéquation , il suffit de prendre les abscisses des points de la parabole qui sont strictement au-dessus de la droite d'équation
La fonction racine carrée est . Il en résulte que est toujours vraie pour tous les réels positifs ou nuls.
Ainsi :

La fonction racine carrée est . Il en résulte que est toujours vraie pour tous les réels positifs ou nuls.
Ainsi :

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.