Résolutions d'inéquations - Exercice 1

Pour tout réel $$x\ne0$$, on a :
$$\frac{1}{x}\ge-\frac{4}{5}$$ équivaut successivement à :
$$\frac{1}{x}+\frac{4}{5}\ge0$$
$$\frac{1\times5}{x\times5}+\frac{4\times x}{5\times x}\ge0$$ . Nous avons tout mis au même dénominateur :
$$\frac{5}{5x}+\frac{4x}{5x}\ge0$$
$$\frac{5+4x}{5x}\ge0$$
Il nous faut maintenant étudier le signe du quotient $$\frac{5+4x}{5x}$$ à l'aide d'un tableau de signe.
Tout d'abord :

$$\red{\text{D'une part :}}$$

$$5+4x=0\Leftrightarrow 4x=-5\Leftrightarrow x=-\frac{5}{4}$$
Soit $$x\mapsto 5+4x$$ est une fonction affine croissante car son coefficient directeur $$a=4>0$$. Cela signifie que la fonction MONTE donc on commencera par le signe $$\left(-\right)$$ puis ensuite par le signe $$\left(+\right)$$ dans le tableau de signe.

$$\red{\text{D'autre part :}}$$

$$5x=0\Leftrightarrow x=\frac{0}{5}\Leftrightarrow x=0$$ . Attention ici, nous savons que $$x=0$$ est une valeur interdite.
Soit $$x\mapsto 5x$$ est une fonction affine croissante car son coefficient directeur $$a=5>0$$. Cela signifie que la fonction MONTE donc on commencera par le signe $$\left(-\right)$$ puis ensuite par le signe $$\left(+\right)$$ dans le tableau de signe.

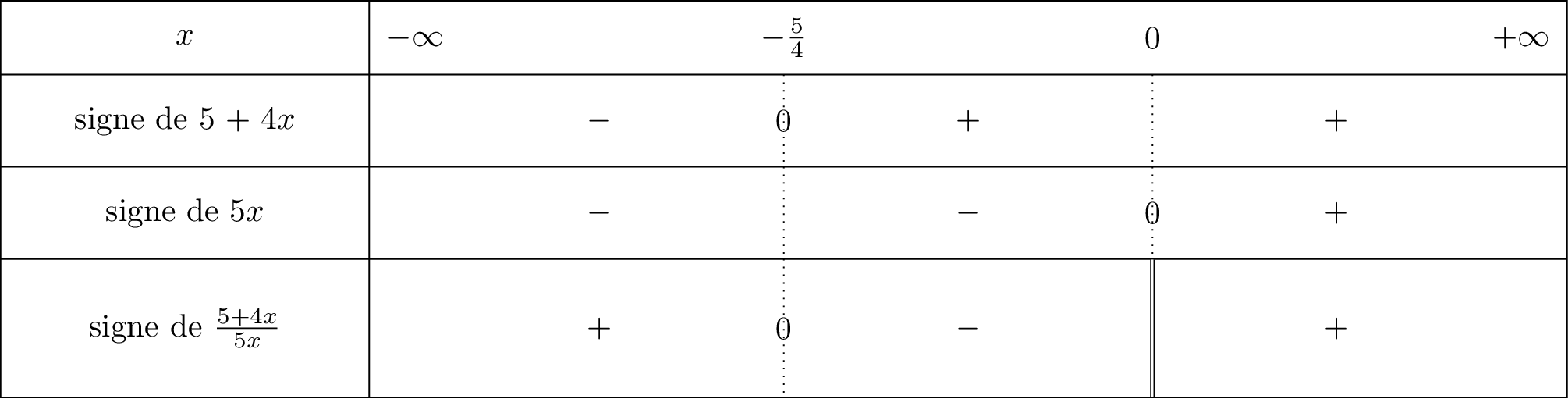L'ensemble des solutions de l'inéquation $$\frac{1}{x}\ge-\frac{4}{5}$$ est