Résolution graphique - Fonction de référence : La fonction carrée $f\left(x\right)=x^{2}$ - Seconde

Question 1

Soit

x

un réel. A l'aide de la représentation de la fonction carré, résoudre graphiquement les inéquations suivantes :

$2\le x^{2}\le5$

Correction

Sur le graphique ci-dessus, nous avons tracé la droite

y=2

et la droite

y=5

. Pour résoudre l'inéquation

2\le x^{2}\le5

, il suffit de prendre les abscisses des points de la parabole

x^{2}

qui sont au dessus ou sur la droite d'équation $y=2$ et qui sont en dessous ou sur la droite $y=5$ .
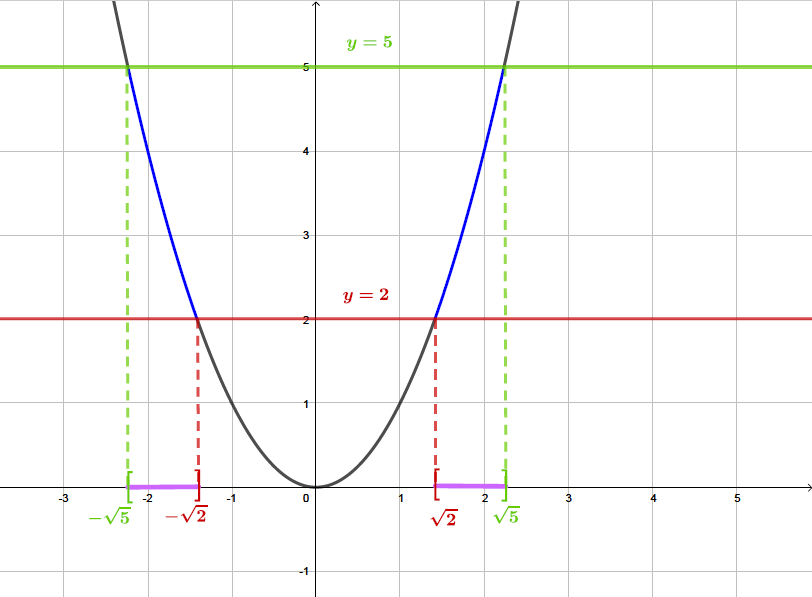
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

S=\left[-\sqrt{5} ;-\sqrt{2} \right]\cup \left[\sqrt{2} ;\sqrt{5} \right]

Question 2

$3\le x^{2}\le6$

Correction

Sur le graphique ci-dessus, nous avons tracé la droite

y=3

et la droite

y=6

. Pour résoudre l'inéquation

3\le x^{2}\le6

, il suffit de prendre les abscisses des points de la parabole

x^{2}

qui sont au dessus ou sur la droite d'équation $y=3$ et qui sont en dessous ou sur la droite $y=6$ .
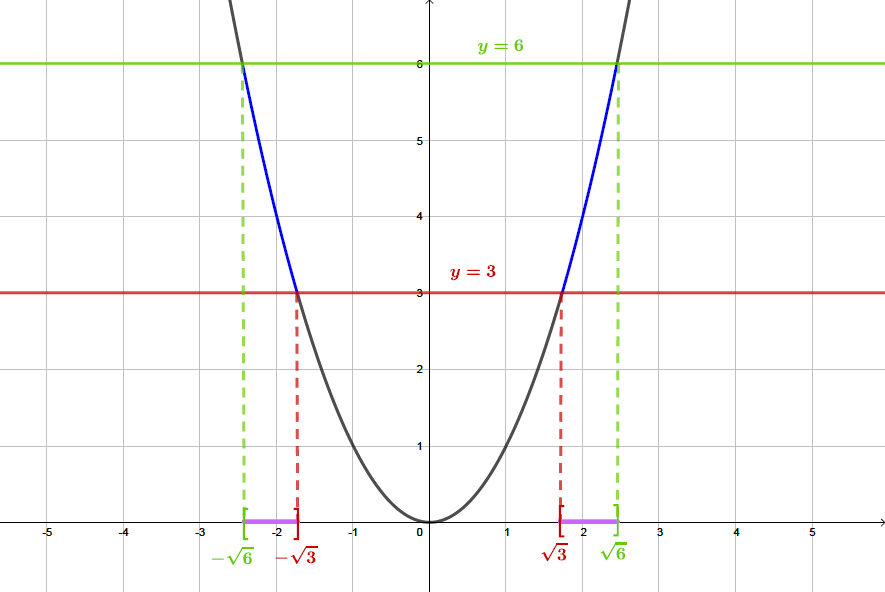
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

S=\left[-\sqrt{6} ;-\sqrt{3} \right]\cup \left[\sqrt{3} ;\sqrt{6} \right]

Question 3

$2\le x^{2}<8$

Correction

Sur le graphique ci-dessus, nous avons tracé la droite

y=2

et la droite

y=8

. Pour résoudre l'inéquation

2\le x^{2}<8

, il suffit de prendre les abscisses des points de la parabole

x^{2}

qui sont au dessus ou sur la droite d'équation $y=2$ et qui sont strictement en dessous de la droite $y=8$ .
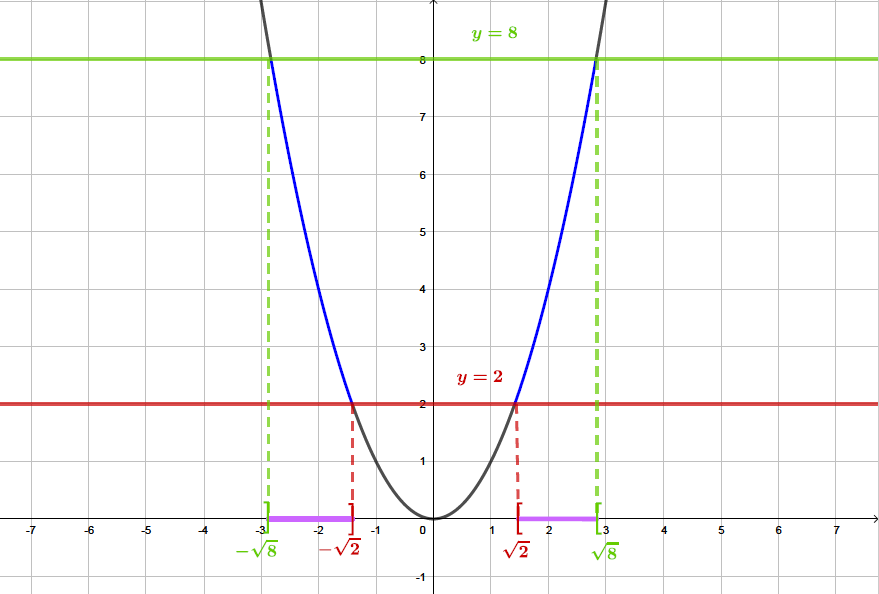
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

S=\left]-\sqrt{8} ;-\sqrt{2} \right]\cup \left[\sqrt{2} ;\sqrt{8} \right[

Question 4

$7< x^{2}<10$

Correction

Sur le graphique ci-dessus, nous avons tracé la droite

y=7

et la droite

y=10

. Pour résoudre l'inéquation

7< x^{2}<10

, il suffit de prendre les abscisses des points de la parabole

x^{2}

qui sont strictement au dessus de la droite d'équation $y=7$ et qui sont strictement en dessous de la droite $y=10$ .
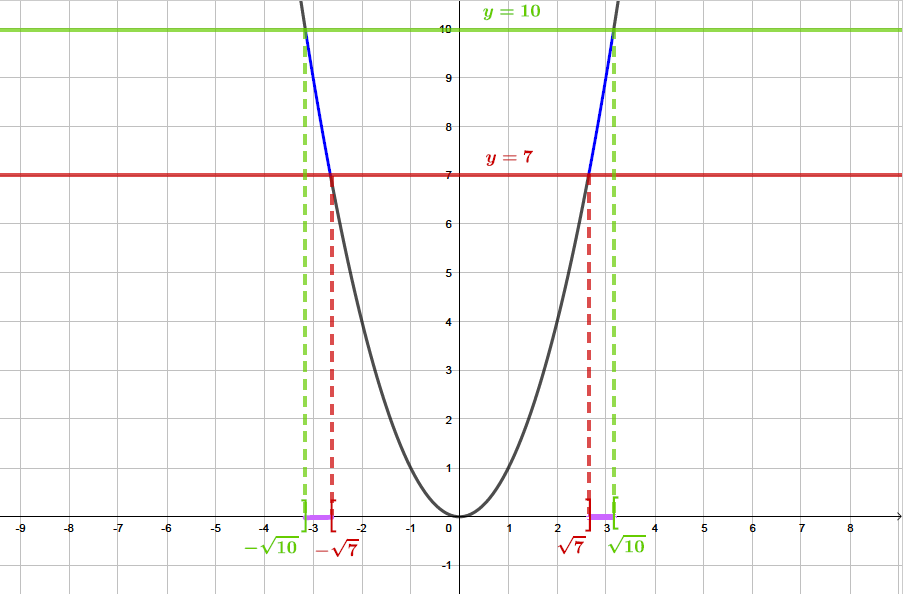
Il s'agit sur le graphique , de la courbe en bleu gras. Les solutions sont représentées sur l'axe des abscisses en violet.
Ainsi :

S=\left]-\sqrt{10} ;-\sqrt{7} \right[\cup \left]\sqrt{7} ;\sqrt{10} \right[

Résolution graphique - Exercice 2

2≤x2≤52\le x^{2}\le52≤x2≤5

3≤x2≤63\le x^{2}\le63≤x2≤6

2≤x2<82\le x^{2}<82≤x2<8

7<x2<107< x^{2}<107<x2<10

$2\le x^{2}\le5$

$3\le x^{2}\le6$

$2\le x^{2}<8$

$7< x^{2}<10$