Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Exercices types : ème partie - Exercice 1
30 min
45
est un parallélogramme. est le point tel que
Les points et sont les milieux respectifs des côtés et .
On considère le repère encore noté
Les points et sont les milieux respectifs des côtés et .
On considère le repère encore noté
Question 1
Faites une figure.
Correction
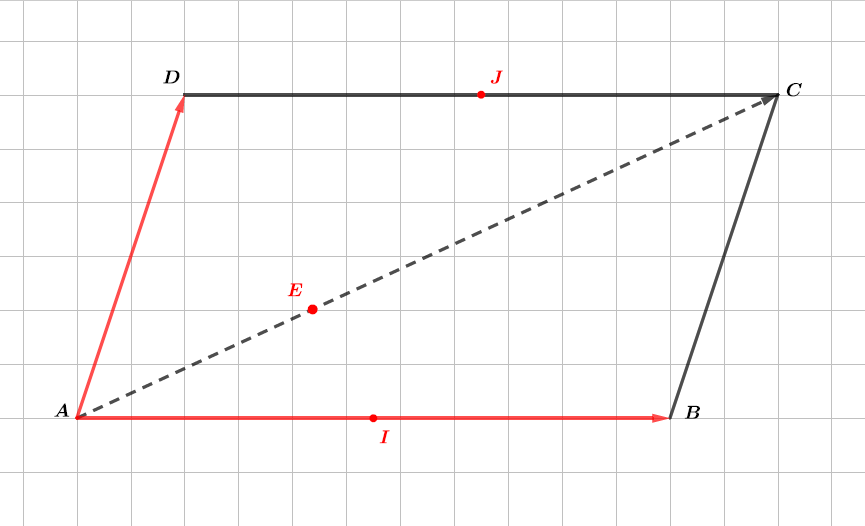
Question 2
Donner, sans justifier, les coordonnées des points , , et dans le repère .
Correction
Dans le repère , on a :
; ; et
; ; et
Question 3
Déterminer les coordonnées des points , et . Justifier.
Correction
est le milieu de donc a pour coordonnées
est le milieu de donc a pour coordonnées
Nous savons que . Or donc .
De plus , d'où : .
Comme cela signifie que
Les coordonnées du point sont alors :
est le milieu de donc a pour coordonnées
Nous savons que . Or donc .
De plus , d'où : .
Comme cela signifie que
Les coordonnées du point sont alors :
Question 4
Montrer que les droites et sont parallèles.
Correction
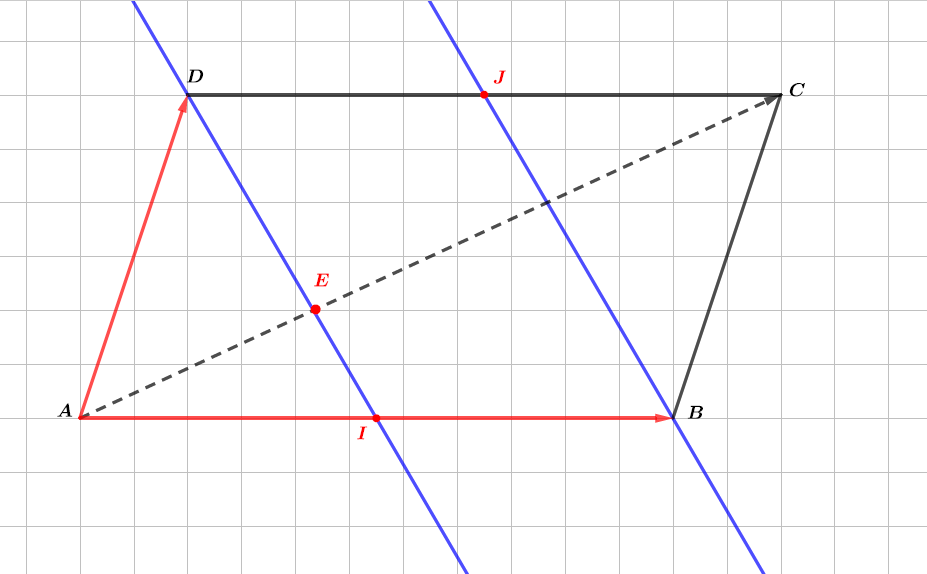
Question 5
Déterminer une équation cartésienne de la droite .
Correction
L'écriture cartésienne d'une droite est de la forme où le vecteur est un vecteur directeur de cette droite.
étant un vecteur directeur de , on en déduit que : et . D'où : et Ainsi , on a : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
Finalement, l'équation cartésienne de la droite est de la forme : .
Question 6
On admet qu'une équation cartésienne de la droite est : et qu'une équation cartésienne de la droite est : .
Montrer que les droites et sont sécantes.
Correction
Deux droites et sont parallèles si leurs vecteurs directeurs respectifs sont colinéaires entre eux. Ainsi :
Soit un vecteur de la droite .
Soit un vecteur de la droite .
Les droites et sont parallèles si et seulement si :
Soit un vecteur de la droite .Soit un vecteur de la droite .
Soit un vecteur de la droite .
Les droites et sont parallèles si et seulement si :
Soit un vecteur de la droite .
Les vecteurs et ne sont pas colinéaires car : .
Les droites et ne sont donc pas parallèles.
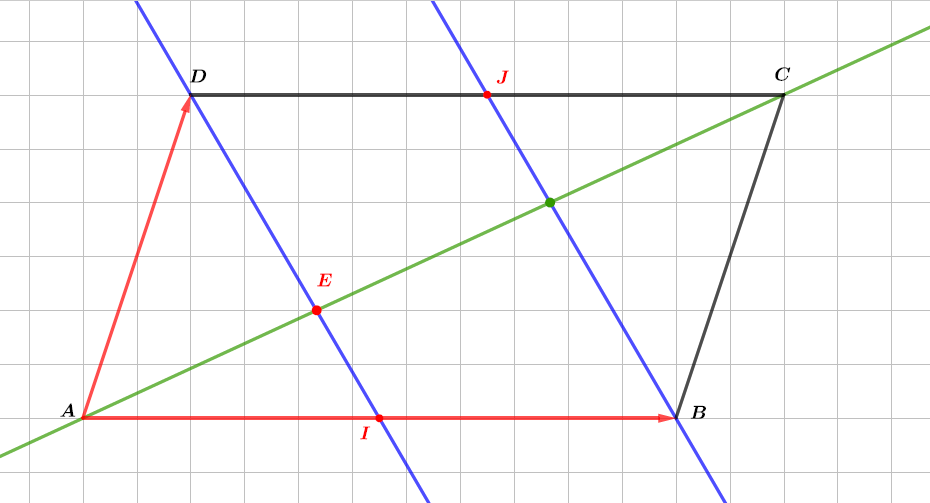
Question 7
Soit le point d'intersection des droites et . Déterminer les coordonnées de .
Correction
Il nous faut résoudre le système suivant :
. Nous pouvons résoudre ce système à l'aide de la méthode par substitution.
Le point d'intersection des droites et est le point de coordonnées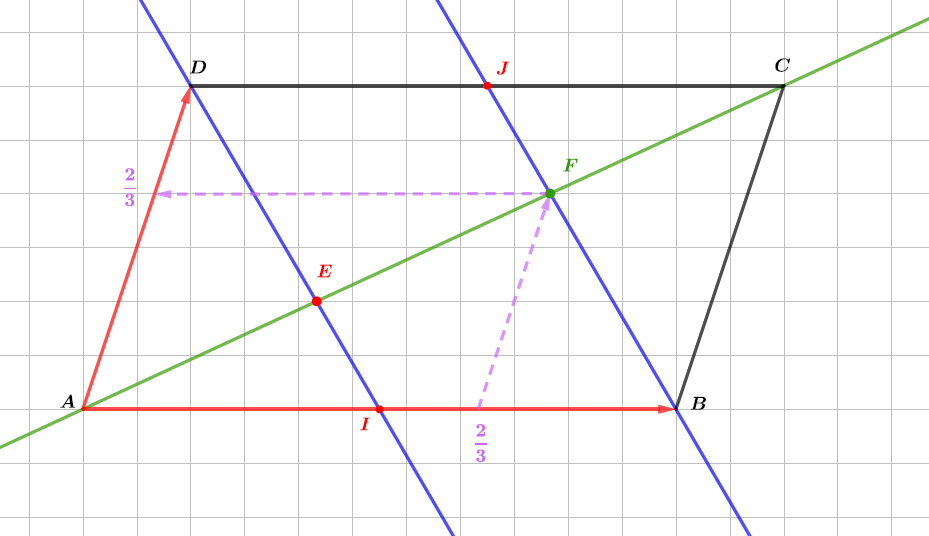
. Nous pouvons résoudre ce système à l'aide de la méthode par substitution.
Le point d'intersection des droites et est le point de coordonnées

Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.