Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Tchat avec un prof
🤔 Bloqué sur un exercice ou une notion de cours ? Échange avec un prof sur le tchat !Découvrir →
Exercices types : ère partie - Exercice 2
30 min
45
On se place dans le repère orthonormal
On donne les points , et .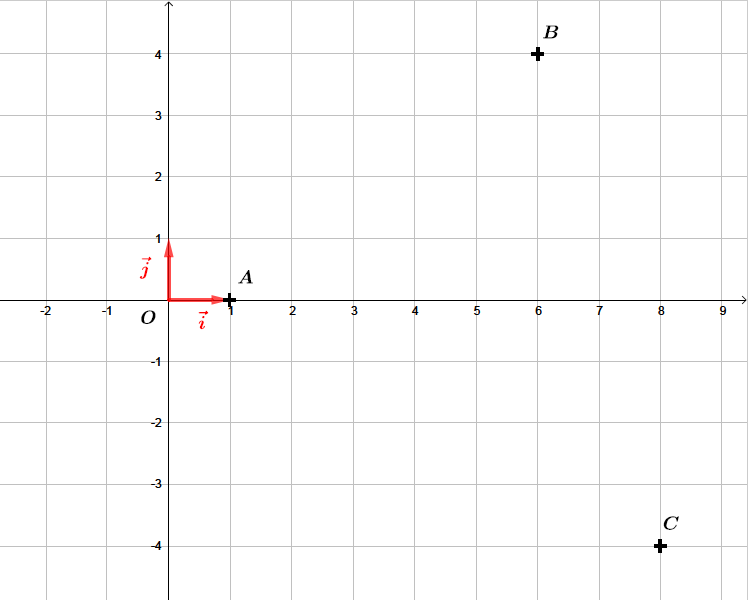
On donne les points , et .

Question 1
Déterminer les coordonnées du milieu de .
Correction
Les coordonnées du milieu de sont : et .
Soit et .
Les coordonnées de sont alors .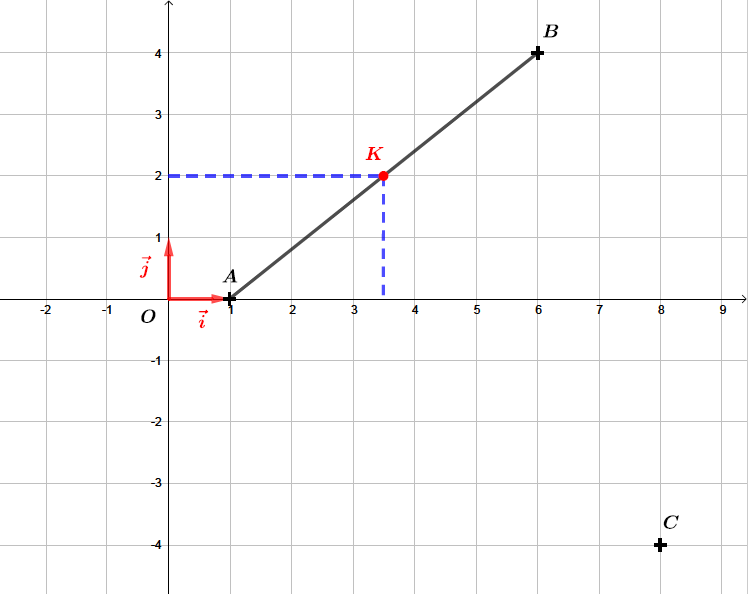
Soit et .
Les coordonnées de sont alors .

Question 2
Déterminer un vecteur directeur de la médiane du triangle passant par .
Correction
La médiane du triangle passant par correspond à la droite .
Ainsi un vecteur directeur de la médiane du triangle passant par est le vecteur .
Soit c'est-à-dire :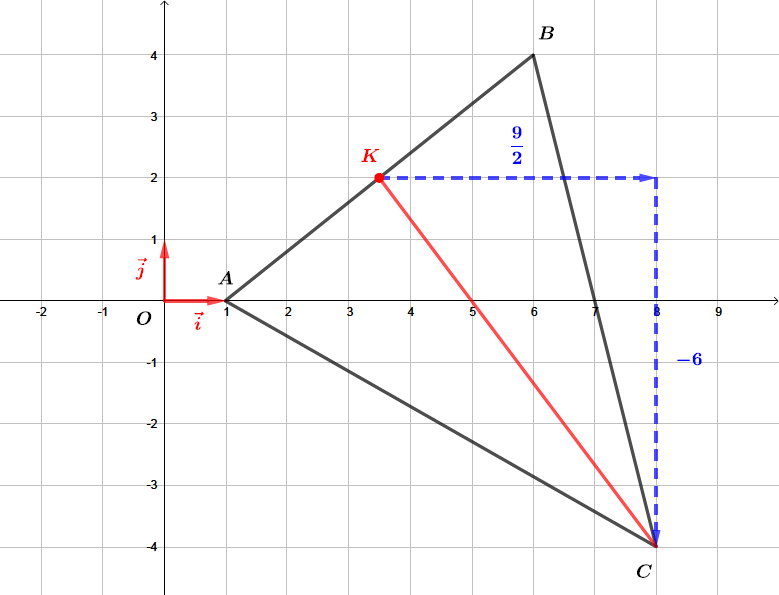
Ainsi un vecteur directeur de la médiane du triangle passant par est le vecteur .
Soit c'est-à-dire :

Question 3
Déterminer une équation de cette médiane.
Correction
étant un vecteur directeur de la droite , on en déduit que : et .
Ainsi, on a : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
L'équation cartésienne de la médiane du triangle passant par est :
Ainsi, on a : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
L'équation cartésienne de la médiane du triangle passant par est :
Question 4
Déterminer une équation de la médiane du triangle passant par .
Correction
Les coordonnées du milieu de sont : et .
Soit et .
Les coordonnées de sont alors .
La médiane du triangle passant par correspond à la droite .
Ainsi un vecteur directeur de la médiane du triangle passant par est le vecteur .
Soit c'est-à-dire :
étant un vecteur directeur de la droite , on en déduit que : et .
Ainsi , on a : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
L'équation cartésienne de la médiane du triangle passant par est : c'est-à-dire
Soit et .
Les coordonnées de sont alors .
La médiane du triangle passant par correspond à la droite .
Ainsi un vecteur directeur de la médiane du triangle passant par est le vecteur .
Soit c'est-à-dire :
étant un vecteur directeur de la droite , on en déduit que : et .
Ainsi , on a : .
Or le point appartient à la droite , donc les coordonnées du point vérifie .
Il vient alors que :
L'équation cartésienne de la médiane du triangle passant par est : c'est-à-dire
Question 5
Déduire des questions précédentes, les coordonnées du centre de gravité de ce triangle.
Correction
Le centre de gravité d'un triangle est l'intersection des médianes.
On cherche alors les coordonnées du point d'intersection de et .Il faut donc résoudre le système suivant :
On remplace dans la ère ligne la valeur de .
Il vient alors que :
Les coordonnées du centre de gravité de ce triangle sont alors :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.