Qui aura 20 en maths ?
💯 Le grand concours 100% Terminale revient le 31 janvier 2026 à l'ESIEA Paris !Découvrir →
Nouveau
🔥 Découvre nos fiches d'exercices gratuites avec corrections en vidéo !Accéder aux fiches →
Manipulations calculatoires - Exercice 1
20 min
40
Cet exercice est un questionnaire à choix multiples (Q. C. M.) . Pour chacune des questions, une seule des quatre réponses est exacte. L'usage de la calculatrice n'est pas autorisé afin de progresser :)
Question 1
L'expression est égale à :
Correction
Ainsi :
Question 2
Soit . L'expression avec un dénominateur sous forme d'entier est :
Correction
- Rendre rationnel un dénominateur signifie que l'on veut écrire le dénominateur sans racines carrées. Pour se faire, on multiplie le numérateur et le dénominateur par l'expression conjuguée du dénominateur. Ainsi le dénominateur fera apparaitre une identité remarquable de la forme qui donne . Ces carrés feront disparaitre les racines carrées au dénominateur.
On a :
équivaut successivement à :
Ainsi :
Question 3
Soient et deux réels non nuls. La forme simplifiée de est :
Correction
- Soient et des réels non nuls.
Finalement :
Question 4
Sans vous préoccuper de l'ensemble de définition de la fonction écrire sous la forme d'un quotient. Ainsi :
Correction
Finalement :
Question 5
Soit un réel. L'équation admet comme solution(s) :
Correction
On reconnait une équation du second degré. On va utiliser le discriminant :
équivaut successivement à :
Comme alors l'équation admet une racine double réelle notée telle que :
ainsi
D'où
La racine de l'équation est donc
Question 6
L'expression est égale à :
Correction
Ainsi :
Question 7
Soient et deux réels. La forme développée de est :
Correction
équivaut successivement à :
Ainsi :
Question 8
On admet que l'expression est définie suivant des valeurs de et que l'on ne cherchera pas à déterminer. La forme simplifiée de est égale à :
Correction
Ainsi :
Question 9
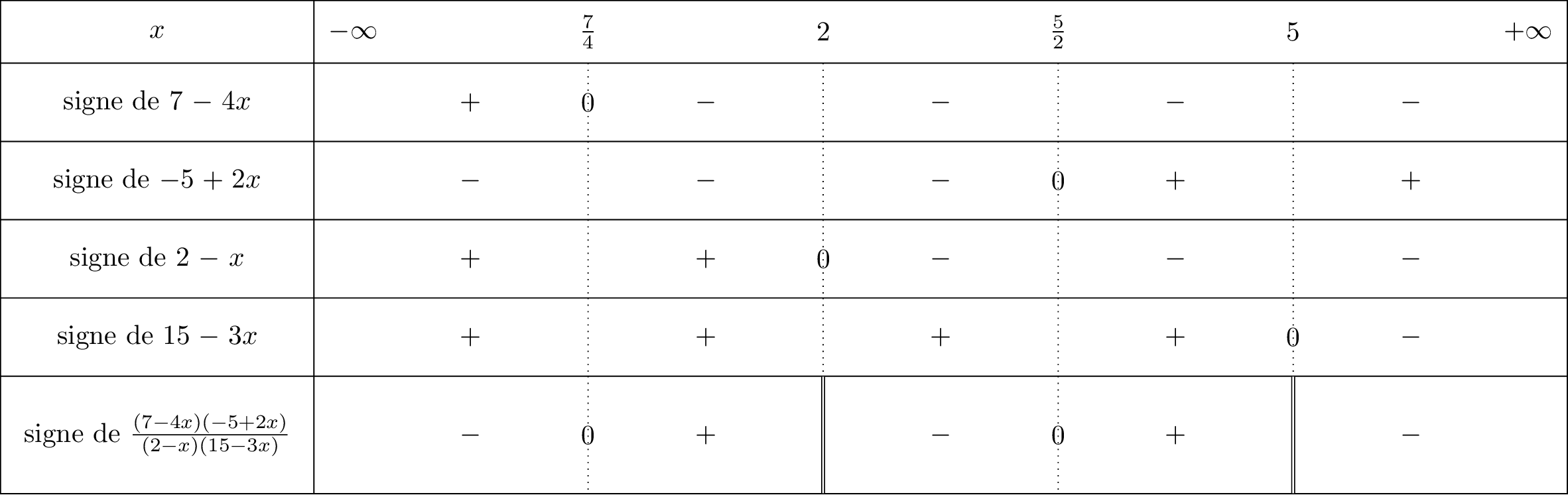
L'ensemble des solutions de l'inéquation est :
Correction
Soit . Nous allons dresser un tableau de signe pour résoudre cette inéquation.
Question 10
L'expression est égale à :
Correction
Ainsi :
Question 11
Soient et deux réels strictement positifs tels que . La simplification de est égale à :
Correction
- Rendre rationnel un dénominateur signifie que l'on veut écrire le dénominateur sans racines carrées. Pour se faire, on multiplie le numérateur et le dénominateur par l'expression conjuguée du dénominateur. Ainsi le dénominateur fera apparaitre une identité remarquable de la forme qui donne . Ces carrés feront disparaitre les racines carrées au dénominateur.
Ainsi :
Question 12
est égale à :
Correction
D'où :
Question 13
La forme simplifiée de est égale à :
Correction
Ainsi :
Nous verrons en première année après le bac la fonction cosinus hyperbolique et la fonction sinus hyperbolique que l'on note respectivement et
Pour tout réel , on a : et
Pour tout réel , on a : et
Question 14
La forme simplifiée de est égale à :
Correction
Ainsi :
Question 15
Soit un réel strictement positif. La forme simplifiée de est égale à :
Correction
Ainsi :
Question 16
Soient , , et quatre réels. Développer .
Correction
équivaut successivement à :
Ainsi :
Question 17
Soit un entier naturel. La forme simplifiée de est égale à :
Correction
équivaut successivement à :
Ainsi :
Signaler une erreur
Aide-nous à améliorer nos contenus en signalant les erreurs ou problèmes que tu penses avoir trouvés.
Connecte-toi ou crée un compte pour signaler une erreur.